高校の数学や物理の勉強で、多くの計算が出ててきます。公式が出てきます。それらの大部分は sf で計算できます。
高校での数学や物理の勉強では、公式を丸暗記するのではなく sf を使って納得できるまで様々の数値実験を行って見てください。単純な計算作業は sf にやらせて、数学や物理の本質を勉強してください。力のある方ならば、このほうが効率的に深く数学や物理を理解できるはずです。
数列は数値を一列に並べたものです。sf のベクトルを数列とみなすことで、高校数学での数列を sf で扱えます。
sf では等差数列を <<...>> の間に、開始:start 大きさ:size 間隔:step の三つの値を指定することで、ベクトルとして表現できます
start@=0,size@=10, step@=1,<< start,size,step>> < 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 >もちろん、数値だけで文字列変数を介在させない式も可能です
seriesTemp = << 0,10,1>> < 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 >
sf 変数に記録してあれば、後で数列:の再確認や和を求めるなど様々の操作が可能です。
seriesTemp # 数列の再確認 < 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 > seriesTemp[3] # 数列要素の確認 < 3 > seriesTemp[<2,3,1>] # 数列部分要素 [2],[3],[4] の取り出し < 2, 3, 4 > !sum(seriesTemp) < 45 > # !sum 関数の引数は sf 式も使えます !sum(<<0,10,1>>) < 45 >
等差数列の 大きさ:size には正の整数しか使えませんが、 ベクトルの和を求める !sum(.) を使えば数列の輪も sf で計算できます。開始:start 間隔:step には複素数までの範囲で任意に指定できます。複素数の等差数列も簡単に作れます。
seriesTemp = << 1+i,10,2i>> < 1+i, 1+3i, 1+5i, 1+7i, 1+9i, 1+11i, 1+13i, 1+15i, 1+17i, 1+19i >
sf では等差数列の式を<<start,size,step @ prm| function(prm)>> のように拡張して、等差数列の要素を関数に与えて得られる数列を定義できます。下のように使います
<< 0,10,1 @k| k^2 + 1>> < 1, 2, 5, 10, 17, 26, 37, 50, 65, 82 >
これを使えば、初期値 a=2 公費 r=1.18 の数列を表す sf ベクトルを下のように計算できます。年利 18% で借りた 2 万円が、十年後には 9 万円弱になることが簡単に判ります。
a@=2, r@=1.18, << 0,10,1 @k| a r^k>> < 2, 2.36, 2.7848, 3.28606, 3.87756, 4.57552, 5.39911, 6.37095, 7.51772, 8.87091 >
python でも似たコードを書けますが、 等比級数となると map だ、lambda だと大掛かりな組み込み機能を使わねばなりません。a, r を global 変数として渡せないのは、この位の小さな規模では、かえって煩わしく感じます。不必要に長いデータを表示するのも困り物です。sf のほうがコンパクト・単純に書けます。重宝します。
//@@ start=0;size=10;step=1 #a=1.18,r=2 print map((lambda k:3*1.18**k),range(start, size*step, step)) //@@@ [3.0, 3.54, 4.1771999999999991, 4.9290959999999995, 5.8163332799999985, 6.8632732703999988 , 8.0986624590719973, 9.5564217017049558, 11.276577608011848, 13.306361577453981]
下のような数列の極限を求める方法を理解するには自分で計算してやることが有効です。
n^2 - n
lim ------------------
n→∞ 3n^2 + n - 2
sf を使えば、下のよう極限を求める計算を簡単に実行できます。n が大きくなれば 1/3 ≒ 0.333333 に近づくのが判ります。
N@=10, <<0,N,10 @n| (n^2-n)/(3n^2+n-2) >> < 0, 0.292208, 0.311987, 0.318915, 0.322447, 0.324589, 0.326027, 0.327059, 0.327835, 0.32844 > # n の増え方を激しくします N@=10, <<0,N,1 @k| n@=2^k, (n^2-n)/(3n^2+n-2) >> < 0, 0.166667, 0.24, 0.282828, 0.306905, 0.319794, 0.326478, 0.329884, 0.331603, 0.332467 > N@=10, <<0,N,1 @k| n@=10^k, (n^2-n)/(3n^2+n-2) >> < 0, 0.292208, 0.328926, 0.332889, 0.333289, 0.333329, 0.333333, 0.333333, 0.333333, 0.333333 >
与式の分母と分子を n^2 で割ることで、を下のように変形してやることでも、極限が 1/3 ≒ 0.333333 に近づくことが判ります
n^2 - n (n^2 - n)/n^2 1 - 1/n
lim ------------------ == lim --------------------- == lim ------------------
n→∞ 3n^2 + n - 2 n→∞ (3n^2 + n - 2)/n^2 n→∞ 3 + 1/n - 2/n^2
分母と分子が 1 と 3 に近づくのを下のように確認するのはやりすぎでしょうか?
N@=10, <<0,N,1 @k| n@=10^k, 1 - 1/n >> < 0, 0.9, 0.99, 0.999, 0.9999, 0.99999, 0.999999, 1, 1, 1 > N@=10, <<0,N,1 @k| n@=10^k, 3 + 1/n - 2/n^2 >> < 2, 3.08, 3.0098, 3.001, 3.0001, 3.00001, 3, 3, 3, 3 >
数学の多くは、実際に計算してやることで理解できます。判らなくて考えているよりは、自分の手で具体例を計算してみるべきです。電卓では手間が掛かりすぎる計算でも sf ならば、エディタ上でコピーして編集するだけで、上のような少しだけの変形された sf 式を容易に計算しなおせます。
下の sf 式で自然対数 e: 2.71828 を実際に計算させられます
e ≡ lim (1+1/n)^n
n→∞
N@=100, << 1,N, 10 @ n | (1+1/n)^n>> < 2, 2.6042, 2.65626, 2.6757, 2.68586, 2.6921, 2.69633, 2.69938, 2.70169, 2.7035, 2.70495, 2.70614, 2.70713, 2.70798, 2.7087, 2.70934, 2.70989, 2.71038, 2.71081, 2.7112, 2.71155, 2.71187, 2.71216, 2.71242, 2.71266, 2.71289, 2.71309, 2.71328, 2.71346, 2.71363, 2.71378, 2.71392, 2.71406, 2.71419, 2.71431, 2.71442, 2.71453, 2.71463, 2.71472, 2.71481, 2.7149, 2.71498, 2.71506, 2.71514, 2.71521, 2.71527, 2.71534, 2.7154, 2.71546, 2.71552, 2.71557, 2.71563, 2.71568,2.71573, 2.71577, 2.71582, 2.71586, 2.71591, 2.71595, 2.71599, 2.71602, 2.71606, 2.7161, 2.71613, 2.71616, 2.7162, 2.71623, 2.71626, 2.71629, 2.71632, 2.71635, 2.71637, 2.7164, 2.71642, 2.71645, 2.71647, 2.7165, 2.71652, 2.71654, 2.71657, 2.71659, 2.71661, 2.71663, 2.71665, 2.71667, 2.71669, 2.7167, 2.71672, 2.71674, 2.71676, 2.71677, 2.71679, 2.71681, 2.71682, 2.71684, 2.71685, 2.71687, 2.71688, 2.7169, 2.71691 >sf が備えている gdsp.bat を使えは収束の様子を、簡単に gnuplot に表示させられます
# gdsp は引数を与えないときは最後のデフォルト計算結果 _dt.val を表示します gdsp
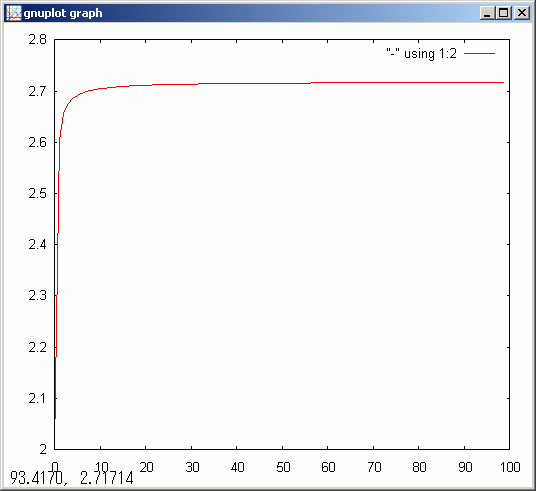
自然対数の底は下の公式でも計算できます
∞
e ≡ Σ1/n! == 1 + 1 + 1/2! + 1/3! + ... + 1/n! + ....
n=0
# 繰り返し関数に複数式を書くとき、| 記号を指定する事で、要素値を最終式以外に変更できます
N @=10, temp@=1,<<1,N,1@k|temp|,temp=temp/k>>
< 1, 1, 0.5, 0.166667, 0.0416667, 0.00833333,
0.00138889, 0.000198413, 2.48016e-005, 2.75573e-006 >
!sum(N @=10, temp@=1,<<1,N,1@k|temp|,temp=temp/k>> )
< 2.71828 >
lim(1+1/n)^n よりも収束がずっと早い事が分かります
sin(x) の微分は下のように定義されます。
sin(x+Δx) - sin(x)
sin(x)' ≡ lim --------------------
Δx=>0 Δx
上式を sf 式で下のように計算できます。x == 0 での微分値を求められます。
x@=0,N@=10, <<0,N,1 @k| Δx@=10^-k, (!sin(x+Δx) - !sin(x))/Δx>> < 0.841471, 0.998334, 0.999983, 1, 1, 1, 1, 1, 1, 1 >
x=0 では Δx= 10^-3 で六桁程度の微分値が得られています。
Δx@=10^-3,N@=64, sin'=<<0,N,2`π/N @x| (!sin(x+Δx) - !sin(x))/Δx>>
gdsp sin'
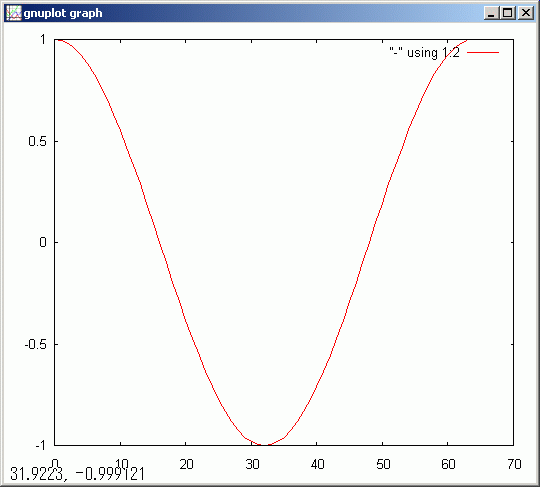
この微分値は cos(x) と小数点以下三桁まで一致しています。sin(x)' == cos(x) だと数値計算から推測されます。
N@=64, sin' - <<0,N,2`π/N @x| !cos(x)>> < -1.66667e-007, -4.91744e-005, -9.77086e-005, -0.000145302, -0.000191496, -0.000235845, -0.000277924, -0.000317325, -0.000353671, -0.000386611, -0.000415827, -0.000441039, -0.000462004, -0.000478519, -0.000490425, -0.000497609, -0.0005, -0.000497576, -0.00049036, -0.000478422, -0.000461876, -0.000440882, -0.000415642, -0.000386399, -0.000353436, -0.000317068, -0.000277647, -0.000235551, -0.000191188, -0.000144983, -9.73817e-005, -4.88427e-005, 1.66667e-007, 4.91744e-005, 9.77086e-005, 0.000145302, 0.000191496, 0.000235845, 0.000277924, 0.000317325, 0.000353671, 0.000386611, 0.000415827, 0.000441039, 0.000462004, 0.000478519, 0.000490425, 0.000497609, 0.0005, 0.000497576, 0.00049036, 0.000478422, 0.000461876, 0.000440882, 0.000415642, 0.000386399, 0.000353436, 0.000317068, 0.000277647, 0.000235551, 0.000191188, 0.000144983, 9.73817e-005, 4.88427e-005 >
一変数関数は sf のベクトル変数の数値の集まりで近似できます。そのベクトルによる関数に対して ~shift(.) したものとの差分を使えば、関数の近似微分を計算できます。sin(.) 関数を例に考えてみましょう。
下のように [0,2`π] を定義域する sin 関数の sf ベクトル変数 vSin を作ります
N@=64, vSin = <<0,N,2`π/N @x| !sin(x)>>
gdsp vSin
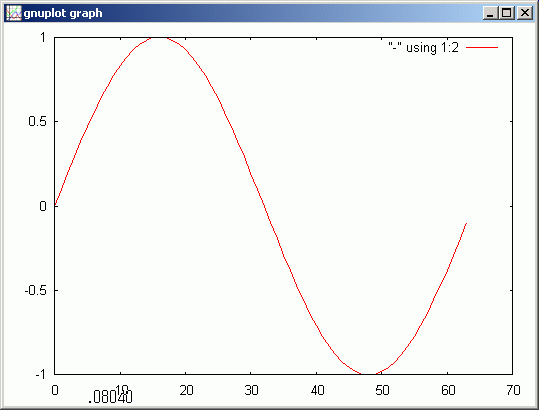
この vSin は shift を使って次のように近似微分できます。
N@=64, Δx@=2`π/N, vSin' = (vSin - ~shift(vSin))/Δx < 0, 0.998394, 0.988779, 0.969642, 0.941166, 0.903626, 0.857384, 0.802885, 0.740654, 0.671289, 0.59546, 0.513896, 0.427383, 0.336755, 0.242883, 0.146672, 0.049048, -0.049048, -0.146672, -0.242883, -0.336755, -0.427383, -0.513896, -0.59546, -0.671289, -0.740654, -0.802885, -0.857384, -0.903626, -0.941166, -0.969642, -0.988779, -0.998394, -0.998394, -0.988779, -0.969642, -0.941166, -0.903626, -0.857384, -0.802885, -0.740654, -0.671289, -0.59546, -0.513896, -0.427383, -0.336755, -0.242883, -0.146672, -0.049048, 0.049048, 0.146672, 0.242883, 0.336755, 0.427383, 0.513896, 0.59546, 0.671289, 0.740654, 0.802885, 0.857384, 0.903626, 0.941166, 0.969642, 0.988779 >
"'" やギリシャ文字上の式のように微分を意味する "'" を変数の最後に加えられたり、やギリシャ文字Δを含む sf 変数名を使えることは、数式の記述で重宝します。sf の小さな自慢です。
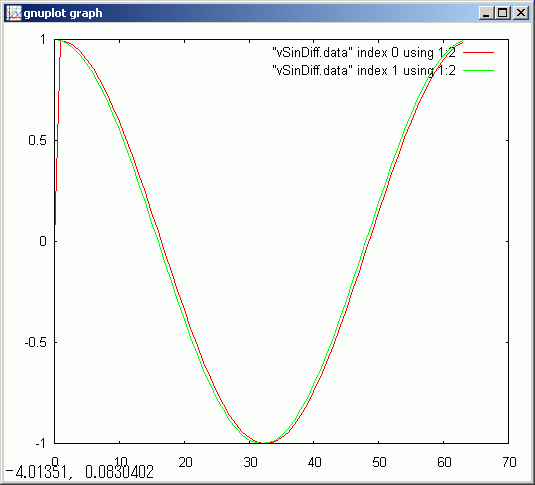
二つのグラフを重ねて表示させる方法上のように gnuplot で二つのグラフを重ねて表示させるには、ここで説明したような細工が必要です
数値微分の精度は良くありません。二桁の精度を期待することに無理があります。でも概略としての傾向を上のグラフのように見るだけで充分なことが良くあります。
物理や工学の分野などでは、このようなラフな近似でも充分や分野も多くあります。普通の抵抗の精度は 5% です。二桁以上の精度で近似しても無意味な回路での計算など多く存在します。このような分野では、ここで行ったような数値微分でも充分に有効です。
sf での ~shift(.) を使った近似微分も活用ください
//@@ N@=64, Δx = (`π/2)/N, !sum( <<0,N,Δx @x| !sin(x) Δx>>) < 0.987678 >64 分割のようなラフな近似計算でも 1.2% 程度の精度の答えが得られます。