電卓実技部門のみのデモです。「デモ自慢」に応募して、こちらに回されました。 sf と名付けた数値計算に特化したソフトのデモ内容を纏めます。
sf は 自分が欲しくて、スクラッチから作りあげた国産ソフトです。行列ベクトル演算も 含む数値計算に特化したソフトです。科学技術計算を効率的に行うことを追求しました。

数式テキスト自体を、そのまま実行させることを目標としています。論文や教科書を読むときなど、エディタ上にあるメモ書きの数式を試行錯誤しながら計算させていくソフトです。python や C 言語など既存の数値演算ライブラリと組み合わせても使える計算ソフトです。python の 1/3 程度のコード量で済みます。
sf は次のような特徴を持っています
sf はこちらからダウンロードください。また sf の詳細な使い方はこちらを参照ください。
「他人の分けの解らないソフトなど使いたくない。」「他人のデバッグに付き合いたくない。」などの御意見もあると思います。でも安心してください。
私は kVerifier と名付けた C/C++ プログラムの検証ライブラリを開発しています。 sf は、この検証ライブラリの適用例でもあります。ソースの大部分を公開しています。カバレッジ 100% のテストができています。このテストも公開しています。
バグがないとは言いませんが、過去に遭遇したバグは全て kVerifier のテストとして蓄積されています。それらが対策されていることを自動確認させています。他人のバグ鳥に付き合わされる可能性は非常に小さくできていると自負しています。
様々の sf 計算コード例を以下に示します。
1+2+3+10+11+12 < 39 > # 純虚数を i で表します。sf での唯一の予約語です。 (1+i)i < -1+i > # `πや `degree を使えます !sin(`π/4)^2 + 3!tan(`π/6)^2 + !cos(24`degree) < 2.41355 > # 真空の誘電率:`ε0 プランク定数:`h` 光速度:`c 素電荷:`eQなどの物理定数が使えます 4 `π `ε0 `h` `c / `eQ^2 < 137.034 > # 微細構造定数
行列 ベクトルの演算を python での行列ベクトルの演算と比較してみます。sf のほうが、よりコンパクトに、また数式に近く記述できることが解ります。また、関数文字列よりも、文字列の入らない行列やベクタの生成記号のほうが数式として見やすくなります。
| 動作 | python コード | sf コード |
| 0 vecotr の生成 | zeros(5) | <<5>> |
| 0.1,2,3,4 vecotr の生成 | arange(0,5) | <<0,5,1>> |
| 1..1 vecotr の生成 | array((1.,)*5) | <<1,5,0>> |
| 0.2,4,6 vecotr の生成 | arange(0.,7.,2) | <<0,4,2>> |
| 7x5 0 行列 の生成 | zeros([7,5], Float64) | [[7,5]] |
| 5x5 0 行列 の生成 | zeros([5,5], Float64) | [[5]] |
| 行列の j 行 | mat[j,:] | mat[j,*] |
| 行列の j 列 | mat[:,j] | mat[*,j] |
| 行列 の対角成分 | [mat[i,i] for i in range(len(mat))] | mat[*,*] |
| 5x5 行列で対角の一つ上の斜め成分 | [mat[i,i+1] for i in range(4)] | mat[<1,4,5>] #スライス アレー引数 |
| 内積 | dot(l, r) | < l|r > |
| 複素ベクタの内積 | dot(l, conjugete(r)) | < l|r > |
| 計量行列付内積 | dot(l, dot(m,r)) | < l|M|r > |
| 計量行列付複素内積 | dot(l, conjugate(dot(m,r))) | < l|M|r > |
| sin(x) 関数ベクタの生成 | [sin(x) for x in arange(0, pi, pi/128)] | N@=128,<<0,N,`π/N @x|!sin(x)>> |
| 行列の生成 |
from numarray import * array([ [x,x+1,x+2,x+3] for x in arange(0.1, 2.1, 1)]) | << 0.1 ,3,1 @x| < x,x+1,x+2,x+3> >> |
| Matrix m の多項式 | m**3 + 2*m**2 + 3*m + 4 | m^3+2m^2+3m+4 |
| インデックス付変数 | 無し | Γ`__{1}[i,j] |
また、sf の数値は double 型の浮動小数点のみです。python 配列のときのように integer 型と Float32, Float64, Complex32,Complex64 などを区別する必要はありません。メモリの無駄遣いと非難されるかもしれませんが、記述の容易さを選択しています。525M byte の実装メモリが普通の現状では、全ての数値を 64bit double に統一する割り切り方も許されるべきです。
python のリスト内包表記に似た形式で、関数ベクトルを生成できます。ただしパラメータの設定が BLESS 流の start, size, step です。こちらの方が数値計算に適します。
これ使って sin 関数の sf ベクトル変数を生成し、fft/rft 組み込み関数を使ってフーリエ変換/逆変換の計算をしてみます。
# デフォルトの _dt.val 変数に 100 次元の sin(x)^2 関数ベクトルデータを出力します。 N@=100, <<0,N,2`π/N @x| !sin(x)^2>>
gnuplot にグラフ表示させます。
# デフォルトでは _dt.val 変数を表示します。 gdsp
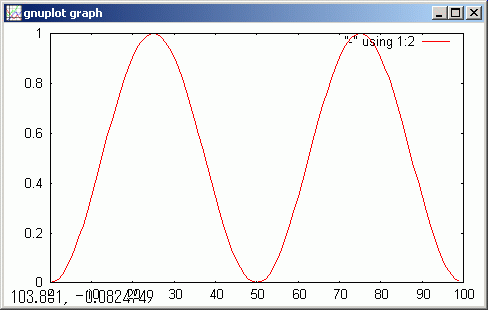
なお、上のグラフで横軸が [0,2`π] ではなく [0,100] になっています。手抜きです。!print(set xtics ("3.142" 90, "6.2" 30) ) などのコマンドにより、横軸の値を設定することもできますが、それよりも簡便に表示するほうが好まれるはずです。使用者には横軸が [0,2`π] であることは自明のはずだからです。
上で計算した sin(x)^2 のデータを fft 変換して real part, image part それぞれをグラフ表示します。
tempF = !fft(_dt) !real(tempF)
gdsp
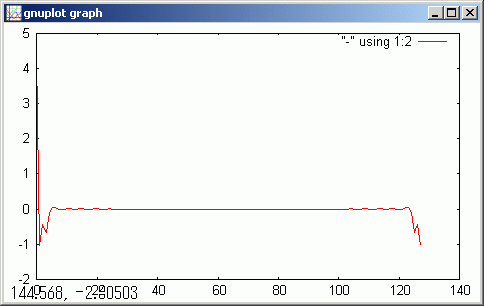
!image(tempF)
gdsp
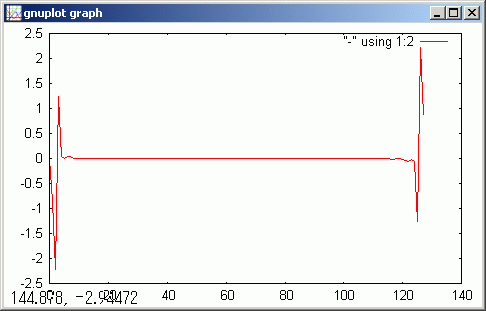
fft データの index 0 から 9 までを 0 に変更し、逆 fft 変換してグラフ表示させます。
tempF[< 0,10,1>] = << 10>> !rft(tempF)
gdsp
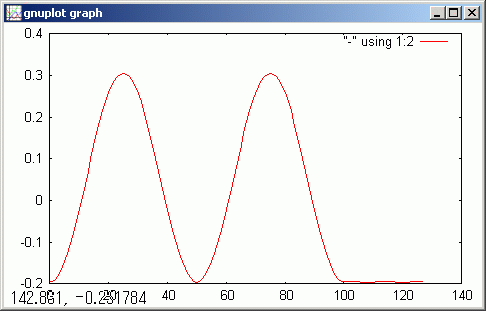
ピーク値が小さくなりました。データを fft 計算のために追加した部分が現れました。そこに小さくデータが染み出しているのが見られます。
量子力学での位置演算子行列 x{size}, 運動量演算子行列 p{size} を作ってやれば量子力学の動作をシミュレートできます。
[-8,8] の位置を離散かした位置演算子をx{16}.val 行列で表現できます。
x{16}
< -7.5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 >
< 0, -6.5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 >
< 0, 0, -5.5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 >
< 0, 0, 0, -4.5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, -3.5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, 0, -2.5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0, -1.5, 0, 0, 0, 0, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0, 0, -0.5, 0, 0, 0, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0, 0, 0, 0.5, 0, 0, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0, 0, 0, 0, 1.5, 0, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2.5, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3.5, 0, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4.5, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5.5, 0, 0 >
< 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 6.5, 0 >
< 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 7.5 >
x{16} をフーリエ変換してやることで、次の運動量演算子 p{16} を得られます。
/p 3,p{16}
< 2.95, -0.196+0.987i, -0.196+0.474i, -0.196+0.294i, -0.196+0.196i, -0.196+0.131i,..
< -0.196-0.987i, 2.95, -0.196+0.987i, -0.196+0.474i, -0.196+0.294i, -0.196+0.196i,..
< -0.196-0.474i, -0.196-0.987i, 2.95, -0.196+0.987i, -0.196+0.474i, -0.196+0.294i,..
< -0.196-0.294i, -0.196-0.474i, -0.196-0.987i, 2.95, -0.196+0.987i, -0.196+0.474i,..
< -0.196-0.196i, -0.196-0.294i, -0.196-0.474i, -0.196-0.987i, 2.95, -0.196+0.987i,..
< -0.196-0.131i, -0.196-0.196i, -0.196-0.294i, -0.196-0.474i, -0.196-0.987i, 2.95,..
< -0.196-0.0813i, -0.196-0.131i, -0.196-0.196i, -0.196-0.294i, -0.196-0.474i, -0.196-0.987i,..
< -0.196-0.0391i, -0.196-0.0813i, -0.196-0.131i, -0.196-0.196i, -0.196-0.294i, -0.196-0.474i,..
< -0.196, -0.196-0.0391i, -0.196-0.0813i, -0.196-0.131i, -0.196-0.196i, -0.196-0.294i,..
< -0.196+0.0391i, -0.196, -0.196-0.0391i, -0.196-0.0813i, -0.196-0.131i, -0.196-0.196i,..
< -0.196+0.0813i, -0.196+0.0391i, -0.196, -0.196-0.0391i, -0.196-0.0813i, -0.196-0.131i,..
< -0.196+0.131i, -0.196+0.0813i, -0.196+0.0391i, -0.196, -0.196-0.0391i, -0.196-0.0813i,..
< -0.196+0.196i, -0.196+0.131i, -0.196+0.0813i, -0.196+0.0391i, -0.196, -0.196-0.0391i,..
< -0.196+0.294i, -0.196+0.196i, -0.196+0.131i, -0.196+0.0813i, -0.196+0.0391i, -0.196,..
< -0.196+0.474i, -0.196+0.294i, -0.196+0.196i, -0.196+0.131i, -0.196+0.0813i, -0.196+0.0391i,..
< -0.196+0.987i, -0.196+0.474i, -0.196+0.294i, -0.196+0.196i, -0.196+0.131i, -0.196+0.0813i,..
この x{16} p{16} sf 行列変数は様々に利用できます。調和振動子の Hamiltonian 行列が下のように作れます
H = x{16}^2 + p{16}^2
この Hamiltonian の固有値は次のように計算できます
~Jacobi(H) < 2.17888, 5.70579, 9.34777, 13.0477, 16.7905, 20.5228, 24.4176, 27.8878, 32.5907, 35.4324, 42.1134, 44.8655, 53.2616, 57.1114, 66.6778, 79.272 >
gdsp # editor で gnuplot.ini ファイルの一行目にある "with line" 文字列を取った後に下を実行させます start wgnuplot
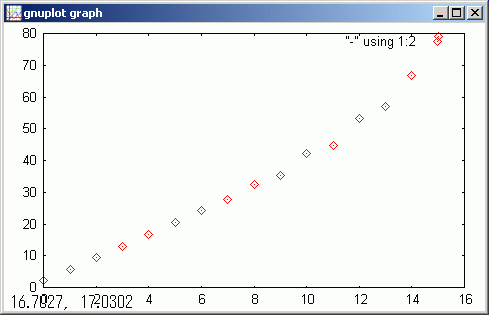
最小の固有値は性値であり 0 ではありません。ゼロ点振動が出てきました。
小さい固有値は一定間隔で直線上に乗ります。固有値が大きくなると自乗カーブに変わります。
時刻 0 で <1,0,....0>> 状態にあるベクトルの時間変化を計算してみます
//@@ /s e @=<<16>> e[0] = 1 N@=10 temp=\ <<0,N, 0.3/N @t| !abs(~expM(t H/i) e) >> //@@@
# メッシュ表示 gspl temp
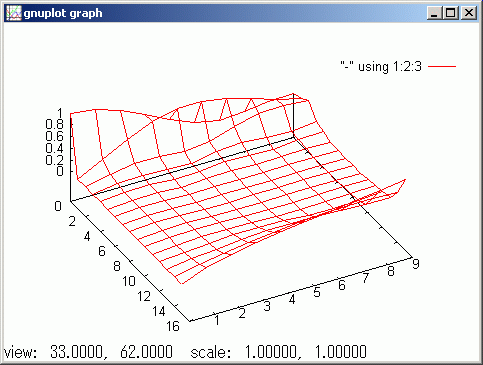
こんな簡単なモデルでも波動関数の拡散と振動が見られます。
ちなみに下のように double:16 桁の数値でも、 t が 0.5 では下のように計算誤差が入り込みます
/p 3,t@=0.5, ~expM(-t H/i) ~expM(t H/i) < 9.68-3.14i, 1.76+0.675i, -0.13-0.55i, 1.5+0.257i, -0.257+0.743i,... < -1.21-2.82i, 1.42-0.449i, -0.31-0.176i, 0.28-0.595i, 0.27+0.0489i,... < 1.06+0.917i, 0.213+0.169i, 0.952-0.00135i, 0.0689+0.0281i, -0.0907+0.0214i,... < 0.803+0.00816i, 0.191-0.0983i, -0.115-0.0415i, 1.03+0.0449i, -0.0357+0.0336i,... < 0.632-0.2i, 0.11-0.000658i, -0.0429+0.0398i, 0.056+0.0449i, 0.947+0.0213i,... < 0.00264-0.634i, -0.00754+0.0764i, 0.0305+0.0359i, 0.0348-0.0309i, 0.0118-0.00583i,... < -0.116-0.0988i, 0.0317+0.0617i, -0.0181+0.0217i, -0.00428+0.0252i, -0.014+0.00584i,... < -0.0136-0.0561i, -6.19e-005-0.0549i, 0.0323+0.00833i, 0.00507-0.00472i, -0.00621-0.00233i,... < -0.12+0.308i, 0.0139+0.0774i, 0.00507+0.0491i, 0.0215+0.0319i, -0.0162+0.00261i,... < 0.353-0.0567i, 0.0327-0.0335i, 0.0808+0.0273i, 0.0963+0.0085i, -0.00255+0.0318i,... < -0.0288-0.54i, 0.186-0.0291i, 0.0994-0.0315i, 0.0521-0.111i, 0.0139+0.0395i,... < 0.019+0.214i, -0.196-0.0727i, -0.00654-0.127i, -0.0613-0.000777i, 0.0212+0.0119i,... < -0.376+1.31i, -0.219+0.359i, 0.0206-0.0313i, -0.199+0.182i, -0.042-0.0969i,... < 0.00889+0.159i, 0.48+0.251i, -0.158-0.132i, 0.0226+0.0636i, -0.0423-0.0522i,... < 4.64+1.2i, 0.699+0.00577i, 0.12-0.0457i, 0.575+0.271i, -0.2+0.216i,... < 7.81-2.64i, 0.599+0.0489i, -0.456-0.141i, 1.3+0.0543i, -0.118+0.886i,...
もし t が 0.3 ならば下のように、7 桁程度の精度で計算されます。
/p 3,t@=0.3, ~expM(-t H/i) ~expM(t H/i) < 1, -1.66e-007-1.55e-007i, 1.2e-008-6.36e-008i, 1.94e-008-1.42e-008i,... < 3.03e-008+7.07e-008i, 1, 4.62e-008+2.55e-008i, -3.79e-009+5.11e-008i,... < 9.33e-008+3.87e-008i, -3.2e-008-2.53e-008i, 1, 1.56e-008+1.29e-008i,... < 7.42e-008-8.4e-008i, -2.11e-008+2.56e-008i, -1.31e-008-6.2e-010i, 1,... < -3.51e-008-6.48e-008i, -1.08e-008+1.34e-008i, -7.83e-009-2.64e-009i, 6.01e-009-4.47e-009i,... < -4.46e-008-1.02e-008i, -5.62e-009+1.6e-008i, 4.06e-010-4.69e-009i, 4.16e-009-4.98e-009i,... < -5.73e-008+8.48e-009i, -8.61e-009+2.99e-009i, -4.06e-009-2.74e-009i, 3.45e-009-1.98e-009i,... < -1.05e-008-1.3e-009i, 9.06e-009+1.03e-008i, -1.37e-010+9.43e-010i, -3.44e-010-5.95e-010i,... < -2.26e-008+2.4e-008i, 1.02e-008+5.71e-009i, -2.81e-009+4.42e-009i, -2.92e-009+7.19e-010i,... < 3.56e-009+2.7e-008i, 5.43e-009-3.35e-010i, -6.02e-009-2.21e-009i, 1.4e-009-4.4e-009i,... < 5.39e-008+1.8e-008i, 3.4e-008+1.92e-008i, -2.37e-009+3.73e-009i, 4.71e-009-2.57e-009i,... < 4.18e-009+2.92e-008i, 1.04e-008-2.73e-008i, 6.35e-009+3.36e-009i, 3.66e-009+8.62e-010i,... < -3.21e-009+4.79e-008i, -1.72e-008-2.84e-008i, -3.37e-008-1.52e-009i, -1.52e-008-1.76e-008i,... < 8.22e-008+4.75e-008i, -7.33e-008+5.44e-008i, -2.39e-008+3.61e-008i, -2.48e-008+1.04e-009i,... < -1.56e-007-1.44e-007i, 8.12e-008+9.93e-008i, 4.86e-008+1.57e-008i, -2.22e-008+1.27e-008i,... < -3.32e-008+8.99e-008i, 3.66e-009-8.33e-008i, -6.4e-008-7.23e-009i, -6.42e-008+7.62e-010i,...
このような誤差が発生するのは、expM(A) = 1 + A^1/1! + A^2/2! + A^3/3! + A^4/4! + ..... + A^n/n! + ... を計算するとき、行列の特定要素 i1, j1 が収束しても他の i, j 要素が収束するとは限らないためです。収束させるために級数の和を取りつづけると既に収束した要素にエラーが回り込むためです。大きな t に対して expM(.) を計算させるときは、行列の他の要素からの計算誤差の回りこみが発生しないように対角化してから expM(.) を計算させるなどの対策が必要です。
sf ユーザー関数を python コードで記述できます。例えば python の gamma 関数を呼び出す sf ユーザ関数を次のように python コードで記述できます。
//@@
# -*- encoding: cp932 -*-
import scipy
import sfVal # sf 変数を読み書き:put/get するモジュールです。
# sf.exe は_arg{1}.val(, arg{2}.val...) の名前の sf 変数ファイルに引数値を設定した後に
# python gamma.py を呼び出します。
_ar = sfVal.getSf('_arg{1}')
# gamma.py の戻り値を sf.exe に知らせるため、_rs.val ファイル変数に関数値を書きこみます。
sfVal.putSf(scipy.array([scipy.special.gamma(_ar[0])]),'_rs')
//@@@
//copy \#####.### gamma.py /y
~gamma.py(2) < 1 > ~gamma.py(4) < 6 > !exp(~gamma.py(2+3i)^3) < 1.00152+0.00109786i >
sf 変数と python numarray.array 変数との間で互いに変換させあうインターフェースが sfVal.py に作ってあります。sfVal.py を使えば python の任意の数値演算機能を sf から利用できます。
sf の BLESS 流パラメータ start, size, step を使ったベクトル/行列の生成は繰り返し処理の記述にも使えます。これにより、微分方程式を数値的に解くことができます。
下に台風の圧力勾配が pressure(r) = pc + Δp!exp(-r0/r) で分布していると仮定し、、また東京の緯度における、単位速度あたりに加わるコリオリの加速度 8.3e-5 `meter/`sec^2 が付け加わったときの 1`meter^3 の空気の塊の軌跡を数値シミュレーションしてみました。コリオリの力が加わると、とても解析的には解けませんが、数値実験ならば容易です。
//@@
/s
mass = 1.18`Kg # 1^meter^3 の空気の質量
cEffct = 8.3e-5 `meter/`sec^2 # 東京の緯度における、単位速度あたりに加わるコリオリのの加速度
Δp= 100(100 `newton/`meter^2) # 100 ヘクト パスカルの気圧差
rFirst @= 300`Km
Δt @= 60*2, v@=<<2>>, point @=<<2>>, r @=< rFirst,0>, r0 @=10`Km, N@=200
α@= Δp r0/!norm(r)^2 !exp(-r0/!norm(r))/mass
v[0] = α Δt/2
<<0, N, Δt @t|\
point = point + v Δt|
r =< rFirst, 0> - point
temp = cEffct < v[1], -v[0]>
α = Δp r0/!norm(r)^2 !exp(-r0/!norm(r))/mass
v = v + (α r/!norm(r) + temp) Δt
>>
//@@@
gdsp
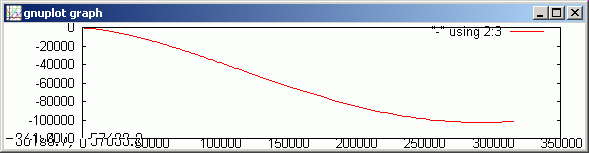
コリオリの力だけでは台風の渦ができないことが分かります。コリオリの力は、少し台風の風の流れを歪めるだけであることが分かります。
実際の台風の風は、コリオリ力と同時に、100 キロメートル以上のの空気の塊が持つ角運動量が、角運動量を保存しながら中心に吸い寄せられることに伴う角速度の増大によるものも大きな要因を占めます。でも、私の能力では、未だその様子を上手くシミュレーションできません。
いずれにせよ sf が微分方程式の数値解を計算することにも有効であることが解ってもらえると思います。
コンピュータの RGB 表示をを活用して、二次元平面上に複素数変面上での複素数分布を表示させられます。下に 0+0i を中心とする複素平面上の複素数値と、RGB ピクセルの対応させ方を「複素数値 kkRGB 地図」として示します。

複素平面上の四角形と行列の i,j 要素を対応させ、i,j 要素に複素解析関数値を入れてやり、この複素数値を、上の kkRGB 地図 の色に対応させてやれば、複素関数値の四次元分布を RGB 画像としてコンピュータ画面上に表示できます。
mkRGB.exe は、このような複素関数の sf 変数を引数に与える事で、その行列すなわち複素関数の kkRGB 表示を行わせるプログラムです。 acos(z) を kkRGB 表示してみます。
//@@
/s
N@=100
temp=<<2,N,-4/N @y|
<<-2,N,4/N @x|
!acos(x+i y)
>>
>>
//@@@
mkRGB temp
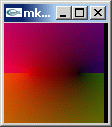
左右にリーマン面が見られます。この不連続なリーマン面は acos(z) が多価関数であることを意味します。皆様も acos(z) 関数の四次元分布をイメージできますでしょうか。
python を使って同じ事を行わせれば、より大きな kkRGB 図の sf 行列変数を高速に得られます。そのようにして下の kkRGB 図を描きました。
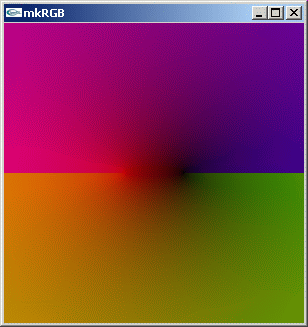
詳細はこちら を見てください。
sf での計算は手計算に似ています。Jacobi.exe や mkRGB.exe などの小物ツールと組み合わせて計算していくソフトです。gnuplot や python など様々のソフトと組み合わせて使っていくソフトです。コンソールから使う CUI ソフトです。近頃の統合環境で使うソフトではありません。でも、この方がコンピュータに慣れた方には使い勝手が良いはずです。sf.exe は重宝するはずです。是非お試し下さい。