�L���v�f�@�͕��������_�ł��B�ł��A�����Ɨ������Ă��Ȃ��ƁA�����̖��ɂɓK�p�����Ƃ��ɁA�����������ËL���Ă��鍂�Z���̂悤�ɓڒ����ȓ����ɂȂ��Ă��܂��댯�������Ă��܂��B���ꂪ�g���Ă����������삷�� fool proof �ȗL���v�f�@�̃\�t�g�͍��Ȃ��ł��傤�B
�L���v�f�@�𗝉����邽�߂ɂ́A�P���Ȗ��𗝘_�ɏ]���������Ōv�Z���Ă݂邱�Ƃ��ǂ����@�ł��B�[���ł���܂ŁA�������������Ɛ��l���������Ă݂�ׂ��ł��B�ł��d��ł͗L���v�f�@�̌v�Z����ɂ͎�Ԃ������肷���܂��B�R���s���[�^�̃v���O���������Όv�Z�̎�Ԃ��Ȃ��܂����A�f�o�b�O�̎�Ԃ�����ȏ�ɂ������Ă��܂��܂��B������ sf �ł��Bsf ���g���A�d��̂悤�Ȍv�Z�̎�Ԃ����������ɁA�v���O�����J���ł̃f�o�b�O�����邱�ƂȂ��A�L���v�f�@�̐��l�������\�ł��B
�ȉ��Asf �ɂ��L���v�f�@�̐��l������ truss �ɓK�p������������Ă����܂��B
�ŏ��ɗL���v�f�@�̕����n�߂��Ƃ��u�g���X�v�f�̗U���v��ǂ݂܂����B������₷���������Ƃɗ͂𒍂��ł��܂��B�L���v�f�@�����߂Ă̕��́A���̐����ł͉������Ƃ��ɁA������̐������ǂ�ł݂Ă��������B
�u�g���X�v�f�̗U���v���Q�Ƃ���Ƃ��y�Ȃ悤�ɁA�u��� 1�v�ɂ��Ă̖��ɂ��ẮA�`�@�A�ޗ��萔���ӎ����ē����ɂ��Ă����܂����B�L�����Ȃ�ׂ���v�����Ă����܂����B
���ʂɒu���ꂽ�_�̗��[�ɗ͂��A�ǂ̂悤�ɕψڂ��邩���l���܂��B�_�̗��[�̈ʒu�ƁA���[�̕ψڂ� Young ���Ɨ��[�ɉ����͂̊W�����߂܂��B��������߂�ƁA�_�̑g�ݍ��킹�ō��ꂽ truss �ł́A�ʂ̖_�v�f�̈ʒu�ƕψڂƗ͂̊W�����`�ɏd�ˍ��킹�����̂Ƃ��āAtruss �Ƃ��đg�ݍ��킳���������ł̊W���܂�
y ��
��
��
�� <x0,y0> <x1,y1> �ʒu
�� �� <Fx0,Fy0> �� <Fx1,Fy1> ��
�� ��������������
�� <Ux0,Uy0> <Ux1,Uy1> �ψ�
��
�������������������������� x ��
��
��
�_�̒f�ʐς� A
������ L
Young ���� E
�Ƃ��܂��B
<Fx0,Fy0, Fx1,Fy1> = E A/L Mat <Ux0,Uy0, Ux1,Uy1> --- (4 ��)
Mat = < 1, 0,-1, 0>
< 0, 0, 0, 0>
<-1, 0, 1, 0>
< 0, 0, 0, 0>
�����ɒu����Ă��邱�ƁA�ނ荇����Ԃɂ��邱�Ƃ���
y0 == y1
Uy0 == Uy1 == 0
Fy0 == Fy2 == 0
�����藧���܂��B
Trus �Ƃ��đg�ݍ��킳������Ԃł��A�ψڂ��������Ƃ��� 4 �������藧���Ă��܂��B�t�ɕψڂ��傫���Ȃ�� 4 �������藧���܂���B�o�l�̂悤�ɉ��{�ɂ��L�т�ό`�� 4 �����Ȃ肽���Ȃ��Ȃ�܂��B�L���v�f�@�ł͂ł�(4 ��)�����藧�Ƃ������ȕψڂ�ΏۂƂ��܂��B
<x0,y0> <x1,y1> �ʒu
�� <Fx0,Fy0> �� <Fx1,Fy1> ��
��������������
y'�� <Ux0,Uy0> <Ux1,Uy1> �ψ�
�^
�^
�_
�_ x'��
�͂ƕψڂ̊W�����̂悤�ɂȂ�܂��B
Rotate = < cos(��), -sin(��), 0, 0>
< sin(��), cos(��), 0, 0>
<0, 0, cos(��), -sin(��)>
<0, 0, sin(��), cos(��)>
# @Rotate(��)^-1 ��ψڂɍ�p�����邱�ƂŁA�_�̎������� x ���ɂȂ�悤�ȍ��W�n�ł̕ψڂ�\���܂�
# @Rotate(��)^-1 ��� �ɍ�p�����邱�ƂŁA�_�̎������� x ���ɂȂ�悤�ȍ��W�n�ł̗� ��\���܂�
Rotate^1 <Fx0,Fy0, Fx1,Fy1> = E A/L Mat Rotate^1 <Ux0,Uy0, Ux1,Uy1>
Mat = < 1, 0,-1, 0>
< 0, 0, 0, 0>
<-1, 0, 1, 0>
< 0, 0, 0, 0>
<Fx0,Fy0, Fx1,Fy1> = E A/L Rotate Mat Rotate^-1 <Ux0,Uy0, Ux1,Uy1> --- (7 ��)
Mat = < 1, 0,-1, 0>
< 0, 0, 0, 0>
<-1, 0, 1, 0>
< 0, 0, 0, 0>
E A/L Rotate^-1 Mat Rotate �̂��Ƃ�v�f�����s��ƌ����܂��BTruss �S�̂ł̍����s��́A���̗v�f�����s�����`�ɑ������킹�Ă�邱�ƂŌv�Z�ł��܂��B�v�f���Ƃ̕ψڂƗ͂̊W����`�ɏd�ˍ��킹����Ԃ� truss �Ŕ������Ă���͂�������ł��B
2
5000mm�^|�� Fx3 == 2000kgf
�@�B�^ |�A
�@�^ | 4000mm
0-------+1
�� �@ ��
3000mm
�f�ʐ�: A=100 mm^2, Young ��: E=21000 Kg/mm^2 �Ƃ��܂�
�����s�� Ke �͐ߓ_ 0,1,2 �̕ψڂɑ��āA�ߓ_ 0,1,2 �ɉ����͂̊W�����߂܂��B
Ke �� 6 x 6 �����s��
�� = Ke * �ψ�
<Fx0,Fy0, Fx1,Fy1, Fx2,Fy2> = Ke <Ux0,Uy0, Ux1,Uy1, Ux2,Uy2>
Ke �����߂邽�߁A�@ �A �B �O�̖_�̗v�f�����s�� Ke1, Ke2, Ke3 �����߂܂��B�܂��A�����Ȗ_�̕ψڂ̍����� �v�Z���� Mat �����܂��B�����ɁA�_�̒f�ʐρAYoung ���� sf �t�@�C���ϐ�: A.val, E.val ���錾���Ă����܂��B
//@@
Mat =[[4]]
Mat[0,*] = < 1, 0, -1, 0 >
Mat[1,*] = < 0, 0, 0, 0 >
Mat[2,*] = < -1, 0, 1, 0 >
Mat[3,*] = < 0, 0, 0, 0 >
A=100 # mm^2 �f�ʐ�
E=21000 # Kg/mm^2 Young ��
//@@@
���� Mat, E, A ���_ �@ �̗v�f�����s�� Ke1 �͉��̗l�ɋ��߂��܂��B
Ke1 �̌v�Z;; L@=3000, Ke1= E A/L Mat
< 700, 0, -700, 0 >
< 0, 0, 0, 0 >
< -700, 0, 700, 0 >
< 0, 0, 0, 0 >
6 x 6 �̍����s�� Ke �̐ߓ_ 0, 1 �ɑΉ����镔���� Ke1 �v�f�������܂��B
//@@
Ke = [[6]]
##�v�f �@ �̕ψ�(�ߓX 0,1)�Ɨ͂̊W�� Ke �ɐݒ肷��
#�v�f �@ �ɂ��� Fx0 �ƕψ� Ux0,Uy0, Ux1,Uy1 �̊W Ke1 ���� Ke �Ɉڂ�
Ke[0,0] = Ke1[0,0]
Ke[0,1] = Ke1[0,1]
Ke[0,2] = Ke1[0,2]
Ke[0,3] = Ke1[0,3]
#�v�f �@ �ɂ��� Fy0 �ƕψ� Ux0,Uy0, Ux1,Uy1 �̊W Ke1 ���� Ke �Ɉڂ�
Ke[1,0] = Ke1[1,0]
Ke[1,1] = Ke1[1,1]
Ke[1,2] = Ke1[1,2]
Ke[1,3] = Ke1[1,3]
#�v�f �@ �ɂ��� Fx1 �ƕψ� Ux0,Uy0, Ux1,Uy1 �̊W Ke1 ���� Ke �Ɉڂ�
Ke[2,0] = Ke1[2,0]
Ke[2,1] = Ke1[2,1]
Ke[2,2] = Ke1[2,2]
Ke[2,3] = Ke1[2,3]
#�v�f �@ �ɂ��� Fy1 �ƕψ� Ux0,Uy0, Ux1,Uy1 �̊W Ke1 ���� Ke �Ɉڂ�
Ke[3,0] = Ke1[3,0]
Ke[3,1] = Ke1[3,1]
Ke[3,2] = Ke1[3,2]
Ke[3,3] = Ke1[3,3]
//@@@
< 700, 0, -700, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0 >
< -700, 0, 700, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0 >
Ke2, Ke3 ����邽�߂ɉ�]���s�킹�� sf �T�u���[�`���E�t�@�C���� Rotate.sf �����܂��B
//@@
@@subFile Rotate # _prm1 is angular of rotation
�� @= _prm{1}
_rt = [[4]]
_rt[0,*] =
_rt[1,*] =
_rt[2,*] = <0, 0, !cos(��), -!sin(��)>
_rt[3,*] = <0, 0, !sin(��), !cos(��)>
@@endSubFile
//@@@
���� Rotate �����g���āA���̗l�� �A �� �B �̗v�f�����s�� KKe2, Ke3 �����܂��B
Ke2 �̌v�Z;; L@=4000, ��=`��/2, Ke2= @Rotate(��) E A/L Mat @Rotate(��)^-1
< 7.6955e-029, -2.01001e-013, -7.6955e-029, 2.01001e-013 >
< -2.01001e-013, 525, 2.01001e-013, -525 >
< -7.6955e-029, 2.01001e-013, 7.6955e-029, -2.01001e-013 >
< 2.01001e-013, -525, -2.01001e-013, 525 >
Ke3 �̌v�Z;; L@=5000, ��@=!acos(3/5), Ke3= @Rotate(��) E A/L Mat @Rotate(��)^-1
< 151.2, 201.6, -151.2, -201.6 >
< 201.6, 268.8, -201.6, -268.8 >
< -151.2, -201.6, 151.2, 201.6 >
< -201.6, -268.8, 201.6, 268.8 >
Ke1,Ke2 �� Ke �̐ߓX 2,3 �ɑΉ�������A�ߓX 0,3 �ɑΉ�������ɑ������킹�܂��B
//@@
##�v�f �A �̕ψ�(�ߓX 1,2)�Ɨ͂̊W�� Ke �ɑ������킹��
Ke[2,2] = Ke[2,2] + Ke2[0,0]
Ke[2,3] = Ke[2,3] + Ke2[0,1]
Ke[2,4] = Ke[2,4] + Ke2[0,2]
Ke[2,5] = Ke[2,5] + Ke2[0,3]
Ke[3,2] = Ke[3,2] + Ke2[1,0]
Ke[3,3] = Ke[3,3] + Ke2[1,1]
Ke[3,4] = Ke[3,4] + Ke2[1,2]
Ke[3,5] = Ke[3,5] + Ke2[1,3]
Ke[4,2] = Ke[4,2] + Ke2[2,0]
Ke[4,3] = Ke[4,3] + Ke2[2,1]
Ke[4,4] = Ke[4,4] + Ke2[2,2]
Ke[4,5] = Ke[4,5] + Ke2[2,3]
Ke[5,2] = Ke[5,2] + Ke2[3,0]
Ke[5,3] = Ke[5,3] + Ke2[3,1]
Ke[5,4] = Ke[5,4] + Ke2[3,2]
Ke[5,5] = Ke[5,5] + Ke2[3,3]
//@@@
< 700, 0, -700, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0 >
< -700, 0, 700, -2.01001e-013, -7.6955e-029, 2.01001e-013 >
< 0, 0, -2.01001e-013, 525, 2.01001e-013, -525 >
< 0, 0, -7.6955e-029, 2.01001e-013, 7.6955e-029, -2.01001e-013 >
< 0, 0, 2.01001e-013, -525, -2.01001e-013, 525 >
//@@
##�v�f �B �̕ψ�(�ߓX 0,2)�Ɨ͂̊W�� Ke �ɑ������킹��
Ke[0,0] = Ke[0,0] + Ke3[0,0]
Ke[0,1] = Ke[0,1] + Ke3[0,1]
Ke[0,4] = Ke[0,4] + Ke3[0,2]
Ke[0,5] = Ke[0,5] + Ke3[0,3]
Ke[1,0] = Ke[1,0] + Ke3[1,0]
Ke[1,1] = Ke[1,1] + Ke3[1,1]
Ke[1,4] = Ke[1,4] + Ke3[1,2]
Ke[1,5] = Ke[1,5] + Ke3[1,3]
Ke[4,0] = Ke[4,0] + Ke3[2,0]
Ke[4,1] = Ke[4,1] + Ke3[2,1]
Ke[4,4] = Ke[4,4] + Ke3[2,2]
Ke[4,5] = Ke[4,5] + Ke3[2,3]
Ke[5,0] = Ke[5,0] + Ke3[3,0]
Ke[5,1] = Ke[5,1] + Ke3[3,1]
Ke[5,4] = Ke[5,4] + Ke3[3,2]
Ke[5,5] = Ke[5,5] + Ke3[3,3]
//@@@
< 851.2, 201.6, -700, 0, -151.2, -201.6 >
< 201.6, 268.8, 0, 0, -201.6, -268.8 >
< -700, 0, 700, -2.01001e-013, -7.6955e-029, 2.01001e-013 >
< 0, 0, -2.01001e-013, 525, 2.01001e-013, -525 >
< -151.2, -201.6, -7.6955e-029, 2.01001e-013, 151.2, 201.6 >
< -201.6, -268.8, 2.01001e-013, -525, 201.6, 793.8 >
��̑���� �@ �A �B �O�̖_�̗v�f�����s���S�đ������킹���̂ŁA�S�̂̍����s�� Ke �����܂�܂����B��̍s��v�f�̒l������Ή�����悤�� Ke �͑Ώ̍s��ł��BKe �̌v�Z�Ɍ�肪�Ȃ����m�F�̈Ӗ��� Ke �̌ŗL�l�� Jacobi.exe �Ōv�Z�����܂�
# �R���\�[���E�R�}���h, kShell ���g������� ctrl O + S
Jacobi Ke
< -1.53392e-013, -8.90445e-014, 1.13341e-014, 478.317, 1205.28, 1606.41 >
�O�̌ŗL�l�������I�� 0 �ł��B����́A���̕��s�ړ��Ɖ�]�̎O���R�x�������ψڂ��s��ɂȂ镨���I�ȏf���Ă��܂��B�r���ő���~�X�����ꍞ�ނƁA�����s��̌U�l�� 0 �łȂ��Ȃ�܂��BJacobi.exe ���g���č����s��̌ŗL�l�����߂邱�Ƃ́A�v�Z�~�X�����肱��ł��Ȃ����Ƃ��m�F����ȒP�ŗL���ȕ��@�ł��B
Ke �����߂�ꂽ���Ƃʼn��̎����g���ĕψڂ���͂����߂��܂��B
�� �x�N�^ = Ke * �ψڃx�N�^
�ł��A�^����ꂽ���́A�̓x�N�^���^�����Ă���Ƃ��̕ψڂ����߂���ł��B������ Ke �ɂ͋t�s���݂��܂���B���̂܂܂ł́A�̓x�N�^����ψڃx�N�^�����߂��܂���B
���̕��s�ړ��Ɖ�]�̎O���R�x���� Ke �̍s�� 0 �ɂ��Ă��܂��B�Ȃ�A�O�̎��R�x���Ȃ����Ă��A�ŗL�l���� 0 ���Ȃ��Ȃ�͂��ł��B
�ߓ_ 0 ���Œ肵�A�ߓ_ 1 �����[���[�Œ肵�܂��B���̂Ƃ��̕ψڂƗ͂������߂� Ke �͎��̂悤�� K �ɕό`����܂��B
//@@
K=Ke
e1 = <<6>>
e1[0]=1
# x0 �̌Œ�
K[0,*] = e1
K[*,0] = e1
# y0 �̌Œ�
K[1,*] = ~shift(e1,1)
K[*,1] = ~shift(e1,1)
# y1 �̌Œ�
K[3,*] = ~shift(e1,3)
K[*,3] = ~shift(e1,3)
//@@@
< 1, 0, 0, 0, 0, 0 >
< 0, 1, 0, 0, 0, 0 >
< 0, 0, 700, 0, -7.6955e-029, 2.01001e-013 >
< 0, 0, 0, 1, 0, 0 >
< 0, 0, -7.6955e-029, 0, 151.2, 201.6 >
< 0, 0, 2.01001e-013, 0, 201.6, 793.8 >
!det(K)
< 5.5566e+007 >
��̂悤�ɋt�s��̑��݂��鍄���s�� K �����܂����BK ���g���Đߓ_ 2 �� x �������� 2000 kgf �̗͂��������Ƃ��̕ψڂ����߂܂�
displacement = K^-1 <0,0, 0,0, 2000,0>
< 0, 0, 1.45851e-015, 0, 20, -5.07937 >
��̌v�Z���ʂ��A2000 kg�d�̗͂����������ƂŁA �ߓ_ 2 �� x ������ 20mm, y ������ -50 mm �ψڂ��Ă��邱�Ƃ�������܂��B�ߓ_ 1 �� x ������ 1.5e-15 �����ψڂ��Ă��܂����A����͕��������_�v�Z�̌덷�ł��B1 �ɔ�ׂ� 15 �����������l�ł���A�����ł��܂��B
�t�ɕψ� displacement ����ߓX 0,1,2 �ɉ����͂����߂��܂�
force = Ke displacement
< -2000, -2666.67, -2.01948e-028, 2666.67, 2000, 9.09495e-013 >
->
�@�E�A�E�B �v�f�����s�� Ke1, Ke2, Ke3 �� 0�E1�E2 �ߓ_�̕ψ� displacement sf �ϐ��Ƃ��Ďc���Ă��܂��B�������g���āA�_ �B �̉��͂� Ke3 �� 0 �� 2 �ߓ_�̕ψڂ���v�Z�ł��܂��B
Ke3 < displacement[0], displacement[1], displacement[4],displacement[5]>
< -2000, -2666.67, 2000, 2666.67 >
->
���̌v�Z�������Ă��������B������͂�Œ�_��ς��Ă݂āA�[���ł���܂ʼn��͂�ψڂ̐��l�������s���Ă݂Ă��������Bsf ���g���Ηe�Ղł�����B
�����܂ł̋c�_�́A��葽�����̖_�̑g�ݍ��킹�Ɋg���ł��܂��B�A�O�̖_�łł��� Trus �Ɍ��肳��܂���B
L34�B 2
3 �^|�� Fx3 == 2000kgf
L14 �C�_ |�A
�@�^ �_| 4000mm
0-------+1
�� �@ ��
3000mm
L14 = 3000 !cos(!acos(3000/5000))
< 1800 >
L34 = 5000-L14
< 3200 >
//@@
Node = [[4,2]]
Node[<0,4*2,1>] = <\
0 , 0, # �ߓ_ 0
3000 , 0, # �ߓ_ 1
3000 , 4000, # �ߓ_ 2
1800 !cos(!acos(3000/5000)), 1800 !sin(!acos(3000/5000))> # �ߓ_ 3
Rod = [[5,2]]
Rod[<0,5*2,1>] = <\
0, 1, # �ߓ_ 0 �� 1 �����Ԗ_
1, 2, # �ߓ_ 1 �� 2 �����Ԗ_
2, 3, # �ߓ_ 2 �� 3 �����Ԗ_
3, 1, # �ߓ_ 3 �� 1 �����Ԗ_
3, 0> # �ߓ_ 3 �� 0 �����Ԗ_
//@@@
//@@
@@subFile Rotate # r1,r2,L ��茈�܂�
_rt = [[4]]
_rt[<0*4+0,2,1>] = <(r2[0]- r1[0])/L, -(r2[1]- r1[1])/L>
_rt[<1*4+0,2,1>] = <(r2[1]- r1[1])/L, (r2[0]- r1[0])/L>
_rt[<2*4+2,2,1>] = <(r2[0]- r1[0])/L, -(r2[1]- r1[1])/L>
_rt[<3*4+2,2,1>] = <(r2[1]- r1[1])/L, (r2[0]- r1[0])/L>
@@endSubFile
@@subFile SetKatKe # p,q ��茈�܂�
Ke[< 2 p N + 2p, 2, 1>] = Ke[< 2 p N + 2p, 2, 1>] +K[<0*4+0, 2,1>]
Ke[< 2 p N + 2q, 2, 1>] = Ke[< 2 p N + 2q, 2, 1>] +K[<0*4+2, 2,1>]
Ke[<(2 p+1) N + 2p, 2, 1>] = Ke[<(2 p+1) N + 2p, 2, 1>]+K[<1*4+0, 2,1>]
Ke[<(2 p+1) N + 2q, 2, 1>] = Ke[<(2 p+1) N + 2q, 2, 1>]+K[<1*4+2, 2,1>]
Ke[< 2 q N + 2p, 2, 1>] = Ke[< 2 q N + 2p, 2, 1>] +K[<2*4+0, 2,1>]
Ke[< 2 q N + 2q, 2, 1>] = Ke[< 2 q N + 2q, 2, 1>] +K[<2*4+2, 2,1>]
Ke[<(2 q+1) N + 2p, 2, 1>] = Ke[<(2 q+1) N + 2p, 2, 1>]+K[<3*4+0, 2,1>]
Ke[<(2 q+1) N + 2q, 2, 1>] = Ke[<(2 q+1) N + 2q, 2, 1>]+K[<3*4+2, 2,1>]
# Dummy return value. Sub file demands _rt value
_rt=0
@@endSubFile
//@@@
//@@
NN@=4
N @= NN * 2 # �ߓ_�� x �ߓ_������
Ke @= [[N]] # temporary �ϐ��ɂ��Ă����Ȃ��Ɖ����Ԃ��̌v�Z���ԂɂȂ��Ă��܂�
<<0,5,1@j|
p = Rod[j,0]
q = Rod[j,1]
r1 @= Node[p,*]
r2 @= Node[q,*]
L @= !norm(r2-r1)
K = E A/L @Rotate() Mat @Rotate()^-1
@SetKatKe()
>>
Ke{8} = Ke
//@@@
< 1120, 560, -700, 0, 0, 0, -420, -560 >
< 560, 746.667, 0, 0, 0, 0, -560, -746.667 >
< -700, 0, 1260, -420, 0, 0, -560, 420 >
< 0, 0, -420, 840, 0, -525, 420, -315 >
< 0, 0, 0, 0, 236.25, 315, -236.25, -315 >
< 0, 0, 0, -525, 315, 945, -315, -420 >
< -420, -560, -560, 420, -236.25, -315, 1216.25, 455 >
< -560, -746.667, 420, -315, -315, -420, 455, 1481.67 >
# �R���\�[���E�R�}���h, kShell ���g������� ctrl O + A
Jacobi Ke{8}
< -1.60424e-013, 3.85179e-014, 1.49755e-013, 328.844, 1004.08, 1185.44, 2306.98, 3020.49 >
���x���A�S�̂̍����s�� Ke{8} �̌ŗL�l�� 3 �� 0 �ɂȂ��Ă��܂��B���͂Ȃ������ł��B
�ߓX 0 ���Œ肵�A�ߓ_ 1 �����[���[�Œ肵�܂��B���̂Ƃ��̍����s�� K �����̗l�Ɍv�Z���܂��B
//@@
K=Ke{8}
e1 = <<8>>
e1[0]=1
# x0 �̌Œ�
K[0,*] = e1
K[*,0] = e1
# y0 �̌Œ�
K[1,*] = ~shift(e1,1)
K[*,1] = ~shift(e1,1)
# y1 �̌Œ�
K[3,*] = ~shift(e1,3)
K[*,3] = ~shift(e1,3)
!det(K)
< 5.5566e+007 >
//@@@
�ߓ_ 2 �� x �������� 2000 kgf �̗͂��������Ƃ��̕ψڂ����߂܂�
displacement = K^-1 <0,0, 0,0, 2000,0, 0,0>
< 0, 0, 2.64339e-016, 0, 20,
-5.07937, 1.71429, 2.28571 >
�V���ɒlj������ߓ_ 3 �ɂ�����͂� 0 �ł��B�ߓ_ 2 �̈ʒu�̕ψڂ͌v�Z�� 1 �Ɠ����ł��B�߂̖_��lj����Ă��A���̏ꍇ�͍����ɂ͉e�����Ȃ����ƂɂȂ�܂����B
��� 2 �ōs���� Node �� Rod ���g�����v�Z�̂�肩���͔ėp���������܂��B�����܂ŏo���オ���Ă���� ��ʓI�� truss �L���v�f�@�̃v���O������ C �Ȃǂō�邱�Ƃ��e�Ղł��傤�B sf �ɂ͍s��̑���� LU �������[�`����� template library �Ƃ��Ď������Ă���܂��B�����𗘗p���Đ���Ɣėp�I�� trust �L���v�f�@�v���O�����̍쐬�Ƀ`�������W���Ă݂Ă��������B
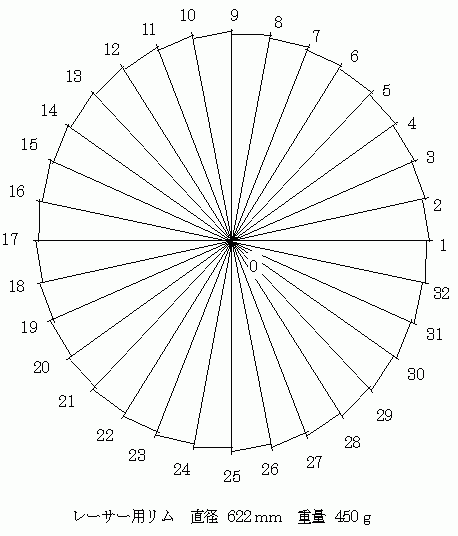
���]�Ԃ̃z�C�[������Ƃ���A���������{�i�I�ȗL���v�f�@�̗��ɒ��킵�܂��Bsf ���\���Ɏ��p�I�ł���Ɣ[�����Ă��炦��͂��ł��B
���̗l�� 32 hole �̃z�C�[�����l���܂��B���ʂɒP�������čl���܂��B

//@@
Node = [[33,2]]
Node[0,*] = <0,0>
r@=622/2, <<0,32,1@j| ��@= 2`��/32, Node[<(j+1)*2,2,1>] = >>
//@@@
�܂� Node �Ԃ̐ڑ������肷�� Rod.val �t�@�C���ϐ������̂悤�ɍ��܂��B
//@@
Rod = [[32 * 2,2]]
Rod[<0,32*2 * 2,1>] = <\
0, 1, 0, 2, 0, 3, 0, 4, 0, 5, 0, 6, 0, 7, 0, 8, 0, 9,
0,10, 0,11, 0,12, 0,13, 0,14, 0,15, 0,16, 0,17, 0,18, 0,19,
0,20, 0,21, 0,22, 0,23, 0,24, 0,25, 0,26, 0,27, 0,28, 0,29,
0,30, 0,31, 0,32,
1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9,10,
10,11, 11,12, 12,13, 13,14, 14,15, 15,16, 16,17, 17,18, 18,19, 19,20,
20,21, 21,22, 22,23, 23,24, 24,25, 25,26, 26,27, 27,28, 28,29, 29,30,
30,31, 31,32, 32, 1>
//@@@
//@@
/s # �o�͂�}�����܂��B�v�Z�𑁂����邽�߂ł��B
NN@=33
N @= NN * 2 # �ߓ_�� x �ߓ_������
Ke @= [[N]] # temporary �ϐ��ɂ��Ă����Ȃ��Ɖ����Ԃ��̌v�Z���ԂɂȂ��Ă��܂�
# �X�|�[�N�����̍����s��̑������킹
# `gH �� < 9.80665 > m/sec^2 �d�͉����x�ł�
E = 2e+5/`gH # 2e+5 N/mm^2 �X�e�����X ���łɈ����苭�� 540N/mm^2
A = 2 # mm^2 14 �Ԑ�
<<0,32,1@j|
p = Rod[j,0]
q = Rod[j,1]
r1 @= Node[p,*]
r2 @= Node[q,*]
L @= !norm(r2-r1)
K = E A/L @Rotate() Mat @Rotate()^-1
@SetKatKe()
>>
# ���������̍����s��̑������킹
# �����̏d�� 450g ���a 622mm, �A���~�̔�d 0.0027g/mm^3 ���f�ʐς��v�Z����
r@=622/2, A = 450 /(2`�� r 0.0027)
E = 7e+4/`gH # 7e+4 N/mm^2 �A���~
<<32,32,1@j|
p = Rod[j,0]
q = Rod[j,1]
r1 @= Node[p,*]
r2 @= Node[q,*]
L @= !norm(r2-r1)
K = E A/L @Rotate() Mat @Rotate()^-1
@SetKatKe()
>>
Ke{33} = Ke
//@@@
# �R���\�[���E�R�}���h, kShell ���g������� ctrl O + A
Jacobi Ke{33}
< -1.32508e-012, -2.98504e-013, 2.65126e-012, 103.816, 103.816, 118.231, 118.231,
123.99, 123.99, 126.785, 126.785, 128.335, 128.335, 129.276,
129.276, 129.885, 129.885, 130.297, 130.297, 130.585, 130.585,
130.789, 130.789, 130.934, 130.934, 131.036, 131.036, 131.103,
131.103, 131.141, 131.141, 131.153, 514.911, 726.969, 726.969,
1902.17, 1902.17, 2262.78, 2262.78, 3697.91, 3697.91, 6128.21,
6128.21, 9093.76, 9093.76, 12478.8, 12478.8, 16152.5, 16152.5,
19973.4, 19973.4, 23794.4, 23794.4, 27468.8, 27468.8, 30855.1,
30855.1, 33823.3, 33823.3, 36259.3, 36259.3, 38069.4, 38069.4,
39184, 39184, 39560.4 >
�ߓ_�ԍ� 25 ���Œ�_�Ƃ��܂��B�ߓX�ԍ� 0 �����z�C�[���̒��S x �����Œ肵�܂��B�z�C�[�������ƌŒ肳��āA�n�u���㉺�ɂ̂ݓ������Ԃł��B
//@@
K=Ke{33}
e1 = <<33*2>>
e1[0]=1
# �ߓX�ԍ� 25 �̌Œ�
K[25*2,*] = ~shift(e1,25*2)
K[*,25*2] = ~shift(e1,25*2)
K[25*2+1,*] = ~shift(e1,25*2+1)
K[*,25*2+1] = ~shift(e1,25*2+1)
# �ߓX�ԍ� 0 �� x ���Œ�
K[0*2,*] = ~shift(e1,0*2)
K[*,0*2] = ~shift(e1,0*2)
//@@@
���]�Ԃ̃z�C�[���̓j�b�v�����ăX�|�[�N�ƃ����̊Ԃɒ��͂�^���܂��B���̒��͂��������� iniTension �Ƃ��ĉ��̂悤�ɐݒ肵�܂��B��{�̃X�|�[�N�� 20 kgf �̒��͂�^������Ԃł��B
iniTension = <<33*2>>
iniTension[<2,32*2,1>] = (f@=20, <<0,32,2`��/32@��| = <-f!cos(��), -f!sin(��)> >>)[<0,32*2,1>]
//@@
iniTension = <<33*2>>
f@=20, <<0,32,1@j| ��@= 2`��/32, iniTension[<(j+1)*2,2,1>] = <-f!cos(j ��), -f!sin(j ��)> >>
//@@@
���̂Ƃ��̕ψ� iniDisplacement �͉��̂悤�Ɍv�Z����܂�
iniDisplacement = K^-1 iniTension
< 0, -0.0388416, -0.0388416, -0.0388416, -0.0380953, -0.0464193,
-0.035885, -0.0537057, -0.0322956, -0.0604209, -0.0274652, -0.0663068,
-0.0215793, -0.0711373, -0.0148641, -0.0747266, -0.00757763, -0.076937,
-2.23779e-015, -0.0776833, 0.00757763, -0.076937, 0.0148641, -0.0747266,
0.0215793, -0.0711373, 0.0274652, -0.0663068, 0.0322956, -0.0604209,
0.035885, -0.0537057, 0.0380953, -0.0464193, 0.0388416, -0.0388416,
0.0380953, -0.031264, 0.035885, -0.0239776, 0.0322956, -0.0172624,
0.0274652, -0.0113765, 0.0215793, -0.006546, 0.0148641, -0.00295664,
0.00757763, -0.000746331, 3.67382e-015, 20, -0.00757763, -0.000746331,
-0.0148641, -0.00295664, -0.0215793, -0.006546, -0.0274652, -0.0113765,
-0.0322956, -0.0172624, -0.035885, -0.0239776, -0.0380953, -0.031264 >
# Node 25 �� y �����̒��͂̒l 20 ���̂��A�Œ�_�̕ψڂƂ��ďo�Ă��Ă��܂��̂� 0 �ɂ��܂�
iniDisplacement[25*2+1] = 0
80 kg �̑̏d�̔������z�C�[���ɂ��������Ƃ��̕ψ� loadDisplacement �͉��̗l�Ɍv�Z����܂�
//@@
load @= <<33*2>>
load[1] = -40
loadDisplacement = K^-1 load
//@@@
< 0, -0.297884,
0.00710324, -0.282864, 0.0044029, -0.283608, 0.00225181, -0.284758, 0.000690955, -0.286132,
-0.000287375, -0.287551, -0.000736685, -0.288848, -0.000750713, -0.289884, -0.000455565, -0.290551,
-7.66464e-016, -0.29078, 0.000455565, -0.290551, 0.000750713, -0.289884, 0.000736685, -0.288848,
0.000287375, -0.287551, -0.000690955, -0.286132, -0.00225181, -0.284758, -0.0044029, -0.283608,
-0.00710324, -0.282864, -0.0102631, -0.282697, -0.0137471, -0.283257, -0.0173795, -0.284659,
-0.0209531, -0.286976, -0.0242395, -0.29023, -0.0270013, -0.294388, -0.0290058, -0.299356,
0, 0, 0.0290058, -0.299356, 0.0270013, -0.294388, 0.0242395, -0.29023,
0.0209531, -0.286976, 0.0173795, -0.284659, 0.0137471, -0.283257, 0.0102631, -0.282697 >
�m�[�h�̔z�u�f�[�^�ƕψڃf�[�^�ł��� sf �ϐ��A Node : loadDisplacement �� iniDisplacement �̓�̕ψڂ� gnuplot �ʼn������܂��Bgnuplot �œ�̃f�[�^���d�ˍ��킹�ĕ\�������邽�߂ɁA�G�f�B�^���g�������Ƃ��K�v�ƂȂ�܂��B
�܂��ŏ��� iniDisplacement �ψڕ������ω������m�[�h�� cdspl �����߂܂��B���� sf ���Ōv�Z���܂��B�ψڗʂ͏��������̂܂ܕ\�����Ă����ʂł��Ȃ��̂ŁA30 �{�̑傫���Ɋg�債�ĕ\�����܂��B
//@@
cdspl = <<33>>
r@=30, <<0,33,1,@I| cdspl[I] = Node[I,0] + r iniDisplacement[2I] + (Node[I,1]+r iniDisplacement[2I+1])i>>
//@@@
�R���\�[���� cdspl �f�[�^�� x �����݂̂�\�������܂��B
gdsp cdspl
�J�����g �f�B���N�g���� gnuplot.ini �t�@�C���ɂ͉��̃f�[�^������������Ă��܂��By ������������Ă��܂��B
# gnuplot.ini �ɂł��Ă���f�[�^
0 0 -1.1652
1 309.83 -1.1652
2 303.88 59.281
3 286.25 117.4
4 257.62 170.97
5 219.09 217.92
6 172.13 256.45
7 118.57 285.08
8 60.446 302.72
9 -4.8091e-014 308.67
10 -60.446 302.72
11 -118.57 285.08
12 -172.13 256.45
13 -219.09 217.92
14 -257.62 170.97
15 -286.25 117.4
16 -303.88 59.281
17 -309.83 -1.1652
18 -303.88 -61.611
19 -286.25 -119.73
20 -257.62 -173.3
21 -219.09 -220.25
22 -172.13 -258.78
23 -118.57 -287.42
24 -60.446 -305.05
25 5.3087e-014 -311
26 60.446 -305.05
27 118.57 -287.42
28 172.13 -258.78
29 219.09 -220.25
30 257.62 -173.3
31 286.25 -119.73
32 303.88 -61.611
���̃R���\�[ gnplot.ini �\���f�[�^�� "0 0 -1.1652" �ȉ��̍s���R�s�[���� wheel.data �Ƀy�[�X�g���܂��B
���l�� 80 Kg �̕��ׂ����������Ƃ��̕ψ� loadDisplacement �̉����f�[�^���쐬���܂��B���� sf ���Ōv�Z���܂��B�����ł��ψڗʂ��A30 �{�Ɋg�債�Ă��܂��B
//@@
cdspl = <<33>>
r@= 30, <<0,33,1,@I| cdspl[I] = Node[I,0] + r (loadDisplacement[2I]+iniDisplacement[2I]) + (Node[I,1]+r (loadDisplacement[2I+1]+iniDisplacement[2I+1]) )i>>
//@@@
�����ł� gdsp cdspl �ɂ���� gnuplot.ini �ɏo�͂��ꂽ���l�f�[�^�� wheel.dat �ɃR�s�[�E�y�[�X�g���܂��B�������A��̃v���b�N�̊Ԃɋ�s��}�����܂��Bgnuplot �œ�̃f�[�^���d�˂ĕ\�����邽�߂ł��B
gdsp cdsp
iniDisplacement �� loadDisplacement ��̕ψڂ��d�ˍ��킹�� Node �̉����f�[�^ wheel.dat �����̂悤�ɍ��܂��B�����œ�̃f�[�^�E�u���b�N�̊Ԃɓ�s�ȏ�̉��s���K�v�ł��B��̉��s�����ł̓G���[�ɂȂ�܂��B�����ӂ�������
# �ŏI�I�� wheel.data
type wheel.data
0 0 -1.1652
1 309.83 -1.1652
2 303.88 59.281
3 286.25 117.4
4 257.62 170.97
5 219.09 217.92
6 172.13 256.45
7 118.57 285.08
8 60.446 302.72
9 -4.8091e-014 308.67
10 -60.446 302.72
11 -118.57 285.08
12 -172.13 256.45
13 -219.09 217.92
14 -257.62 170.97
15 -286.25 117.4
16 -303.88 59.281
17 -309.83 -1.1652
18 -303.88 -61.611
19 -286.25 -119.73
20 -257.62 -173.3
21 -219.09 -220.25
22 -172.13 -258.78
23 -118.57 -287.42
24 -60.446 -305.05
25 5.3087e-014 -311
26 60.446 -305.05
27 118.57 -287.42
28 172.13 -258.78
29 219.09 -220.25
30 257.62 -173.3
31 286.25 -119.73
32 303.88 -61.611
0 0 -10.102
1 310.05 -9.6512
2 304.01 50.772
3 286.32 108.86
4 257.64 162.39
5 219.08 209.29
6 172.11 247.79
7 118.55 276.39
8 60.432 294
9 -7.1085e-014 299.95
10 -60.432 294
11 -118.55 276.39
12 -172.11 247.79
13 -219.08 209.29
14 -257.64 162.39
15 -286.32 108.86
16 -304.01 50.772
17 -310.05 -9.6512
18 -304.19 -70.092
19 -286.66 -128.23
20 -258.14 -181.84
21 -219.71 -228.86
22 -172.86 -267.49
23 -119.38 -296.25
24 -61.316 -314.03
25 5.3087e-014 -311
26 61.316 -314.03
27 119.38 -296.25
28 172.86 -267.49
29 219.71 -228.86
30 258.14 -181.84
31 286.66 -128.23
32 304.19 -70.092
�Ō�ɁA�d�˂��\�����s�킹�邽�߂ɃR�}���h���̂悤�� gnuplot.ini �t�@�C�������A gnuplot ���N�����܂��B
type gnuplot.ini
plot "wheel.data" index 0 using 2:3,\
"wheel.data" index 1 using 2:3
start wgnuplot
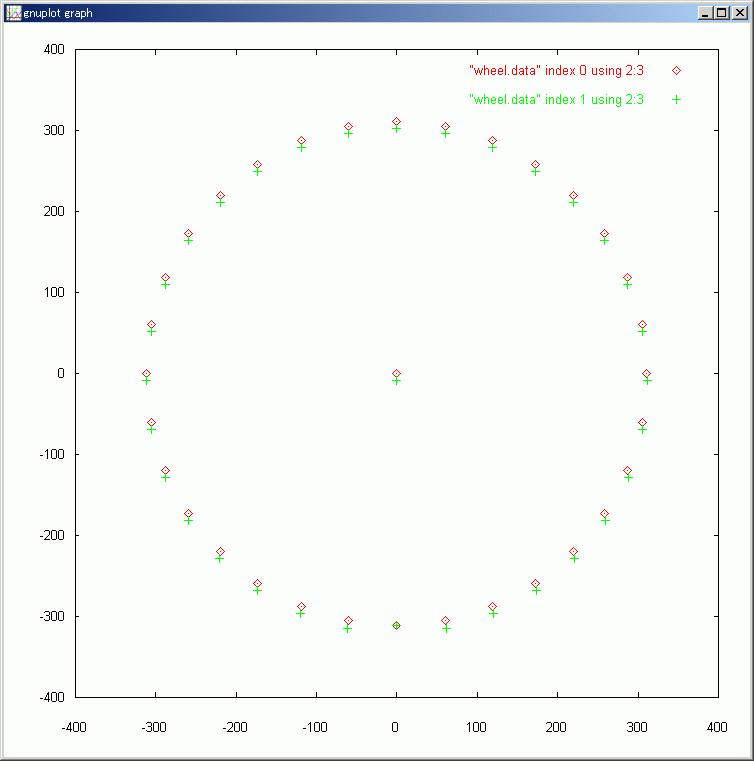
��肪������̂̓z�C�[���̒��S���Œ�_�Ƃ����Ƃ��ł��B�����ߓ_�ԍ� 0 ���Œ�_�Ƃ��܂��B�����Đߓ_�ԍ� 1 �� x �����Œ肵�܂��B�n�u�����Œ肳��āA��]���Ȃ���Ԃł��B
//@@
K=Ke{33}
e1 = <<33*2>>
e1[0]=1
# �ߓX�ԍ� 0 �̌Œ�
K[ 0*2,*] = ~shift(e1, 0*2)
K[*, 0*2] = ~shift(e1, 0*2)
K[ 0*2+1,*] = ~shift(e1, 0*2+1)
K[*, 0*2+1] = ~shift(e1, 0*2+1)
# �ߓX�ԍ� 1 �� x ���Œ�
K[1*2,*] = ~shift(e1,1*2)
K[*,1*2] = ~shift(e1,1*2)
//@@@
�ł��A���̂Ƃ��̍����s�� K �̌ŗL�l�ɂ́A��̂悤�� 0 �������Ă��܂��B�t�s���܂���B
Jacobi K
< 2.37243e-013, 1, 1, 1, 59.9609, 61.8562, 103.816, 105.18,
118.231, 118.993, 123.99, 124.453, 126.785, 127.092, 128.335, 128.552,
129.276, 129.435, 129.885, 130.006, 130.297, 130.391, 130.585, 130.658,
130.789, 130.846, 130.934, 130.978, 131.036, 131.068, 131.103, 131.123,
131.141, 131.15, 501.212, 805.571, 831.335, 1877.91, 1902.17, 3675.4,
3697.91, 6107.5, 6128.21, 9075.01, 9093.76, 12462.2, 12478.8, 16138.2,
16152.5, 19961.4, 19973.4, 23784.8, 23794.4, 27461.4, 27468.8, 30849.8,
30855.1, 33819.9, 33823.3, 36257.3, 36259.3, 38068.5, 38069.4, 39183.8,
39184, 39560.4 >
���Ȃ݂ɁA���̂��炢�̃T�C�Y�ɂȂ�Ƌt�s��̗L���̔���ɍs�̒l�͎g���܂���B�s�̒l�͉��̂悤�ɑ傫�Ȓl�ɂȂ�܂��B��̌ŗL�l�� 1e-13 �̏������ł��A���̗v�f�� 10^3 �̃I�[�_�[�Ȃ�A��������̗v�f�̐ς��v�Z�����Ƃ��ɂ͑傫�Ȓl�ɂȂ��Ă��܂�����ł��B
!det(K)
< -1.72551e+181 >
�ςł��B�O�̎��R�x���S�������̂ł�����AK �̌ŗL�l�� 0 �����荞�ނ̂��s�v�c�Ȃ��Ƃł��B�|�|�|�|�|�|�| ���� "�ߓ_�ԍ� 1 �� x �����Œ肵�܂��B�n�u�����Œ肳��āA��]���Ȃ���Ԃł�" �Ƃ������ɂ���܂����B"�ߓ_�ԍ� 1 �� y �����Œ肵�܂��B�n�u�����Œ肳��āA��]���Ȃ���Ԃł�" �Ƃ���ׂ��������̂ł��B���ہA���̂Ƃ��̍����s��̌ŗL�l�� 0 �͓����Ă��܂���B
//@@
K=Ke{33}
e1 = <<33*2>>
e1[0]=1
# �ߓX�ԍ� 0 �̌Œ�
K[ 0*2,*] = ~shift(e1, 0*2)
K[*, 0*2] = ~shift(e1, 0*2)
K[ 0*2+1,*] = ~shift(e1, 0*2+1)
K[*, 0*2+1] = ~shift(e1, 0*2+1)
# �ߓX�ԍ� 1 �� x ���Œ�
K[1*2+1,*] = ~shift(e1,1*2+1)
K[*,1*2+1] = ~shift(e1,1*2+1)
//@@@
# �R���\�[�����s
Jacobi K
< 1, 1, 1, 22.1727, 59.9609, 89.7092, 103.816, 113.837, 118.231, 122.264, 123.99, 125.984,
126.785, 127.919, 128.335, 129.044, 129.276, 129.75, 129.885, 130.217, 130.297, 130.537, 130.585, 130.761,
130.789, 130.918, 130.934, 131.028, 131.036, 131.099, 131.103, 131.14, 131.141, 131.153, 514.911, 561.285,
831.335, 1245.31, 1902.17, 2691.68, 3697.91, 4817.95, 6128.21, 7531.17, 9093.76, 10724, 12478.8, 14272.7,
16152.5, 18040.5, 19973.4, 21882.3, 23794.4, 25650.5, 27468.8, 29200.1, 30855.1, 32394.7, 33823.3, 35111.5,
36259.3, 37246.1, 38069.4, 38716.5, 39184, 39466 >
�l�������Ă݂�ΐߓ_ 1 �� x �������̎��R�x�������S�����Ă��A�܂��z�C�[���ɂ͉�]�̎��R�x���c���Ă��܂����B�ł�����O�̍S��������^���������ł͍����s�� K �̌ŗL�l�� 0 �ɂȂ�ꍇ�����邱�ƂɂȂ�܂��B����ς蕨���I�������������Ă��Ȃ��Ǝ��s���܂��B
���̂��Ƃ́A����ɎO�̍S��������^���邾���ł́A�����s��̋t�s�M�p�ł��Ȃ����Ƃ����邱�Ƃ��Ӗ����܂��B�z�C�[���̂悤�ȋK���I�ŒP���ȂƂ��́A�t�s�v�Z�ł��Ȃ��Ȃ��ĕςȂ��Ƃ�����܂����B�ł��A�Ȃ܂��t�s�v�Z�ł��Ă��܂��悤�ȋK���I�ł͂Ȃ��z�u�̂Ƃ��͌������Ă��܂����͂��ł��B�S���������{���ɕ����I�ɍS���ł��Ă��邩���肵�Ȃ���Ȃ�Ȃ���Ƃ��ď����Ă����܂��B