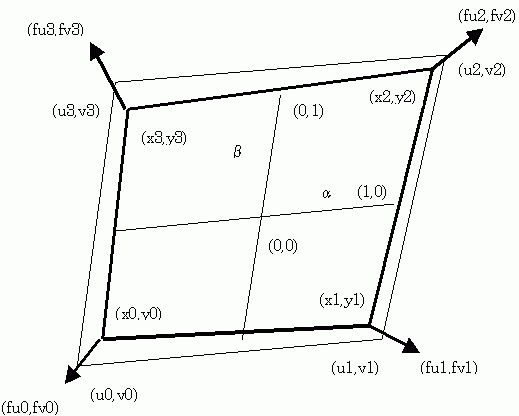
四角形の四つの頂点 (x0,y0), (x1,y1), (x2,y2), (x3,y3) が与えられたとき、α,б∈[-1,1] に対応する、四角形内の位置 (x,y) が下のように表されます。
四角形剛性要素の変移を横位置αと縦位置βの二つのパラメータで表現します。それを元に四角形剛性要素の剛性行列を Ke を導きます。全体を四角形要素に分解し、それぞれの剛性行列を足し合わせて全体の校正行列を導きます。
まず最初に、一つの四角形要素に注目して、四つの頂点に加わっている力と歪と応力の関係式を導きます。
(x0,y0), (x1,y1), (x2,y2), (x3,y3) の位置に頂点をもつ四角形を考えます。その頂点に (fx0,fy0), (fx1,fy1), (fx2,fy2), (fx3,fy3) の力が加わったとの変移を (u0,v0), (u1,v1), (u2,v2), (u2,v2) とします。下に示す、変移と力の関係を表す、一つの四角形要素についての剛性行列 Ke を計算します。
力 == 剛性行列 * 変移
< fx0,fy0, fx1,fy1, fx2,fy2, fx3,fy3> == Ke * <u0,v0, u1,v1, u2,v2, u3,y3>
でも、trus のときのように棒ではなく、平面に分布している四角形に応力が分布していることによって発生する力を求めることになります。四角形の応力分布を求めることが必要になります。このためにα∈[-1,1) β∈[-1,1] のパラメータを使います。そして α、βパラメーターによる変移がもたらす応力分布の式を作ってやり、その式をαとβで積分してやることで、四角形に加わる力を計算できるようにします。
まず α、βの、二つのパラメータによって、(x0,y0),(x1,y1),(x2,y2),(x3,y3) の四点で囲まれる四角形の中の任意の点 (x,y) を下のように表現できます。

四角形の四つの頂点 (x0,y0), (x1,y1), (x2,y2), (x3,y3) が与えられたとき、α,б∈[-1,1] に対応する、四角形内の位置 (x,y) が下のように表されます。
//@@ x0 = 0, y0=0 x1 = 2, y1=0 x2 = 2, y2=1 x3 = 0, y3=1 #α= -1, β=-1 α= 1, β=1 x = 1/4((1-α)(1-β)x0 + (1+α)(1-β)x1 + (1+α)(1+β)x2 + (1-α)(1+β)x3) # α、β∈[-1,1] y = 1/4((1-α)(1-β)y0 + (1+α)(1-β)y1 + (1+α)(1+β)y2 + (1-α)(1+β)y3) //@@@この (x,y) に対する α、βによる J: Jacobian は下の式になります。
∂(x, y )
----------- = J: Jacobian 行列
∂(α, β)
J == 1/4( -(1-β)x0 + (1-β)x1 + (1+β)x2 - (1+β)x3), 1/4( -(1-β)y0 + (1-β)y1 + (1+β)y2 - (1+β)y3)
1/4( -(1-α)x0 - (1-α)x1 + (1+α)x2 + (1+α)x3), 1/4( -(1-α)y0 - (1-α)y1 + (1+α)y2 + (1+α)y3)
位置 (x,y) と同様に、四角形内の変移 (u,v) も α、β のパラメータで表現されます
u = 1/4((1-α)(1-β)u0 + (1+α)(1-β)u1 + (1+α)(1+β)u2 + (1-α)(1+β)u3) # α、β∈[-1,1) v = 1/4((1-α)(1-β)v0 + (1+α)(1-β)v1 + (1+α)(1+β)v2 + (1-α)(1+β)v3) ただし (uj,vj) j=0,1,2,3 は (xj,yj) の位置での変移とします。(u,v) に対する α、βによる J4:Jacobian は下の式になります。
<∂u/∂α, ∂u/∂β> == J <∂u/∂x, ∂u/∂y>
<∂v/∂α, ∂v/∂β> == J <∂v/∂x, ∂v/∂y>
<∂u/∂α, ∂u/∂β,∂v/∂α, ∂v/∂β> == J4 <∂u/∂x, ∂u/∂y ,∂v/∂x, ∂v/∂y>
ただし J4 = | J , 0, 0 |
| 0, 0 |
| 0, 0, |
| 0, 0, J |
より具体的な式にします
<∂u/∂α, ∂v/∂α, u/∂β, ∂v/∂β> ==
|-(1-β)/4, 0, (1-β)/4, 0, (1+β)/4, 0, -(1+β)/4, 0 |*<u0,v0, u1,v1, u2,v2, u3,v3>
| 0, -(1-β)/4, 0, (1-β)/4, 0, (1+β)/4, 0, -(1+β)/4|
|-(1-α)/4, 0,-(1+α)/4, 0, (1+α)/4, 0, (1-α)/4, 0 |
| 0, -(1-α)/4, 0,-(1+α)/4, 0, (1+α)/4, 0, (1-α)/4|
== Form_uv * <u0,v0, u1,v1, u2,v2, u3,v3>
== Form_uv * displacement
但し
Form_uv ≡ |-(1-β)/4, 0, (1-β)/4, 0, (1+β)/4, 0, -(1+β)/4, 0 |
| 0, -(1-β)/4, 0, (1-β)/4, 0, (1+β)/4, 0, -(1+β)/4|
|-(1-α)/4, 0,-(1+α)/4, 0, (1+α)/4, 0, (1-α)/4, 0 |
| 0, -(1-α)/4, 0,-(1+α)/4, 0, (1+α)/4, 0, (1-α)/4|
displacement ≡ <u0,v0, u1,v1, u2,v2, u3,v3>
一方で平面応力を発生させる平面歪率:εx, εy, センダン歪率:εxy と変移率 ∂u/∂x, u/∂y, ∂v/∂x, ∂v/∂y には下の関係があります
<εx, εy, εxy> == εuv <∂u/∂x, u/∂y, ∂v/∂x, ∂v/∂y>
εuv ≡ | 1, 0, 0, 0 |
| 0, 0, 0, 1 |
| 0, 1, 1, 0 |
また平面応力:<σx, σy, σxy> と歪率 εx, εy, εxy は Young 率 E と Poisson 比 μ によって下のように関係付けられます
<σx, σy, σxy> == D * <εx, εy, εxy>
但し
D = | 1, μ, 0 | E/(1-μ^2)
| μ, 1, 0 |
| 0, 0, (1-μ)/2 |
上に述べた行列 From_uv、εuv, D を使って、変移 displacement と四角形の四隅に加わる力を導きます。
displacement = <u0,v0, u1,v1, u2,v2, u3,v3> の変移がある状態で α、β の位置にある dx dy の微小面積には、下に示す応力が発生しています。
<σx, σy, σxy> = D εuv J4^-1 Form_uv displacement
この変移にさらに δuv = <δu0,δv0, δu1,δv1, δu2,δv2, δu3,δv3> の変移が加わると、 下のエネルギーが追加されます。
<εuv J4^-1 Form_uv δuv | <σx, σy, σxy> > dx dy == <δuv |!dggr(Form_uv)!dggr(J4^-1)!dggr(εuv) D εuv J4^-1 Form_uv| displacement > dx dy
この dx dy 微小領域に蓄えられたエネルギー全体、すなわち積分値と、四点に加わる力 F = <Fx0,Fy0, Fx1,Fy1, Fx2,Fy2, Fx3,Fy3> が四つの頂点で発生する変移によってなされる仕事は同じです。
<δuv| F>
==∫<δuv |!dggr(Form_uv)!dggr(J4^-1)!dggr(εuv) D εuv J4^-1 Form_uv| displacement > dx dy
==∫<δuv |!dggr(Form_uv)!dggr(J4^-1)!dggr(εuv) D εuv J4^-1 Form_uv| displacement > !det(J) dα dβ
δuv は任意ですから、下の式が成り立ちます。
F ==∫!dggr(Form_uv)!dggr(J4^-1)!dggr(εuv) D εuv J4^-1 Form_uv displacement !det(J) dα dβ
≒
!dggr(Form_uv)!dggr(J4^-1)!dggr(εuv) D εuv J4^-1 Form_uv displacement !det(J)
(at α=-1/√3 β = -1/√3)
+ !dggr(Form_uv)!dggr(J4^-1)!dggr(εuv) D εuv J4^-1 Form_uv displacement !det(J)
(at α=+1/√3 β = -1/√3)
+ !dggr(Form_uv)!dggr(J4^-1)!dggr(εuv) D εuv J4^-1 Form_uv displacement !det(J)
(at α=-1/√3 β = +1/√3)
+ !dggr(Form_uv)!dggr(J4^-1)!dggr(εuv) D εuv J4^-1 Form_uv displacement !det(J)
(at α=+1/√3 β = +1/√3)
== K * displacement
ただし K ==
!dggr(Form_uv)!dggr(J4^-1)!dggr(εuv) D εuv J4^-1 Form_uv !det(J) (at α=-1/√3 β = -1/√3)
+ !dggr(Form_uv)!dggr(J4^-1)!dggr(εuv) D εuv J4^-1 Form_uv !det(J) (at α=+1/√3 β = -1/√3)
+ !dggr(Form_uv)!dggr(J4^-1)!dggr(εuv) D εuv J4^-1 Form_uv !det(J) (at α=-1/√3 β = +1/√3)
+ !dggr(Form_uv)!dggr(J4^-1)!dggr(εuv) D εuv J4^-1 Form_uv !det(J) (at α=+1/√3 β = +1/√3)
上では「ガウスの積分公式」を使い面倒な積分計算を、四点の足し算で近似計算しています。
上の式によって、四角形要素の要素剛性行列 K を計算できるようになりました。この要素剛性行列を線形に足し合わせてやれば全体の剛性行列が出てきます。
|3 2
|■-------------+
| |
| |1000mm
|■-------------+
|0 2000mm 1 ↓2000 kgf
t=1`mm, E=21000`Kg/`mm^2, μ=0.3 #Poisson ratio
//@@
@@subFile J
_rt =[[2]]
_rt[0,*] = <(-(1-β)x0 + (1-β)x1 + (1+β)x2 - (1+β)x3)/4
, (-(1-β)y0 + (1-β)y1 + (1+β)y2 - (1+β)y3)/4>
_rt[1,*] = <(-(1-α)x0 - (1+α)x1 + (1+α)x2 + (1-α)x3)/4
, (-(1-α)y0 - (1+α)y1 + (1+α)y2 + (1-α)y3)/4>
@@endSubFile
@@subFile J4
_rt = [[4]]
_rt[<0+0*4, 2,1>] = (@J())[0,*]
_rt[<0+1*4, 2,1>] = (@J())[1,*]
_rt[<2+2*4, 2,1>] = (@J())[0,*]
_rt[<2+3*4, 2,1>] = (@J())[1,*]
@@endSubFile
@@subFile Form_uv
_rt = [[4,8]]
_rt[0,*] = < -(1-β)/4, 0, (1-β)/4, 0, (1+β)/4, 0, -(1+β)/4, 0 >
_rt[1,*] = < 0, -(1-β)/4, 0, (1-β)/4, 0, (1+β)/4, 0, -(1+β)/4>
_rt[2,*] = < -(1-α)/4, 0,-(1+α)/4, 0, (1+α)/4, 0, (1-α)/4, 0 >
_rt[3,*] = < 0, -(1-α)/4, 0,-(1+α)/4, 0, (1+α)/4, 0, (1-α)/4>
@@endSubFile
//@@@
後は、四つの頂点の位置、板厚 t, Youn 率 E、Poisson 比 μの値を与えて、εuv, D, 行列を作って理論をなぞって剛性行列を計算します。下のように計算します。
//@@
# εuv @= [[3,4]]
εuv = [[3,4]]
εuv[0,*] = <1,0,0,0>
εuv[1,*] = <0,0,0,1>
εuv[2,*] = <0,1,1,0>
t=1
E = 21000
μ = 0.3
D=[[3]]
D[0,*]=<1,μ, 0> E/(1-μ^2)
D[1,*]=<μ,1, 0> E/(1-μ^2)
D[2,*]=<0,0,(1-μ)/2> E/(1-μ^2)
x0=0, y0=0
x1=2000, y1=0
x2=2000, y2=1000
x3=0 , y3=1000
B=[[3,8]]
α@=-0.57735, β@=-0.57735
B = εuv @J4()^-1 @Form_uv()
K00= !dggr(B) D B t !det(@J())
α =+0.57735, β =-0.57735
B = εuv @J4()^-1 @Form_uv()
K10= !dggr(B) D B t !det(@J())
α =+0.57735, β =+0.57735
B = εuv @J4()^-1 @Form_uv()
K11= !dggr(B) D B t !det(@J())
α =-0.57735, β =+0.57735
B = εuv @J4()^-1 @Form_uv()
K01= !dggr(B) D B t !det(@J())
Ke = K00 + K10 + K01 + K11
//@@@
剛性行列の計算結果は下のようになります
sf command argment: Ke = K00 + K10 + K01 + K11
< 5192.31, 3750, -3173.08, -288.462, -2596.16, -3750, 576.924, 288.462 >
< 3750, 20769.2, 288.462, 2307.7, -3750, -10384.6, -288.462, -12692.3 >
< -3173.08, 288.462, 5192.31, -3750, 576.924, -288.462, -2596.16, 3750 >
< -288.462, 2307.7, -3750, 20769.2, 288.462, -12692.3, 3750, -10384.6 >
< -2596.16, -3750, 576.924, 288.462, 5192.31, 3750, -3173.08, -288.462 >
< -3750, -10384.6, -288.462, -12692.3, 3750, 20769.2, 288.462, 2307.7 >
< 576.924, -288.462, -2596.16, 3750, -3173.08, 288.462, 5192.31, -3750 >
< 288.462, -12692.3, 3750, -10384.6, -288.462, 2307.7, -3750, 20769.2 >
Jacobi.exe Ke
< -8.58628e-012, -1.21176e-012, 6.72659e-014, 5192.3, 10205.2,
20192.3, 20769.2, 47487.1 >
Ke の固有値も、三つが 0 であり、物理的自由度の理屈に合っています。理論どおりに計算できたようです。
//@@
K=Ke
e0=<1,0,0,0, 0,0,0,0>
K[0,*] = e0
K[*,0] = e0
K[1,*] = ~shift(e0,1)
K[*,1] = ~shift(e0,1)
K[6,*] = ~shift(e0,6)
K[*,6] = ~shift(e0,6)
K[7,*] = ~shift(e0,7)
K[*,7] = ~shift(e0,7)
//@@@
< 1, 0, 0, 0, 0, 0, 0, 0 >
< 0, 1, 0, 0, 0, 0, 0, 0 >
< 0, 0, 5192.31, -3750, 576.924, -288.462, 0, 0 >
< 0, 0, -3750, 20769.2, 288.462, -12692.3, 0, 0 >
< 0, 0, 576.924, 288.462, 5192.31, 3750, 0, 0 >
< 0, 0, -288.462, -12692.3, 3750, 20769.2, 0, 0 >
< 0, 0, 0, 0, 0, 0, 1, 0 >
< 0, 0, 0, 0, 0, 0, 0, 1 >
出来上がった K の逆行列を使って 2000 kgf 負荷が、頂点 1 の位置に加わったときの変移 displacement を計算します。
displacement = K^-1 <0,0, -2000 ,0, 0,0, 0,0> # 力による変移量の計算
< 0, 0, -0.569989, -0.21171, 0.200382, -0.173475, 0, 0 >
逆に、変移:displacement と剛性行列:Ke から各頂点に加わる力:force を計算します。
force = Ke displacement
< 2000, 397.059, -2000, -4.54747e-013, 4.54747e-013, 4.54747e-013, -1.27187e-012, -397.059 >
!sum(force)
< 3.97904e-013 >
頂点に加わる四つの力が釣り合っています。頂点四つの力の要素全部を足し合わせると、理屈どおりに 0 になっています。応力の表れ方をみても、物理的直感に一致します。剛性行列の計算に誤りは紛れ込んでいなようです。
|3 2 5 |●------+------+ | | | | 1| |1000mm |●------+------+ |0 1m 1m 4↓2000kgf t=1`mm, E=21000`Kg/`mm^2, μ=0.3 #Poisson ration
//@@
x0@=0, y0@=0
x1@=1000, y1@=0
x2@=1000, y2@=1000
x3@=0 , y3@=1000
t@=1
E @= 21000
μ @= 0.3
D=[[3]]
D[0,*]=<1,μ, 0> E/(1-μ^2)
D[1,*]=<μ,1, 0> E/(1-μ^2)
D[2,*]=<0,0,(1-μ)/2> E/(1-μ^2)
α@=-0.57735, β@=-0.57735
B = εuv @J4()^-1 @Form_uv()
K00= !dggr(B) D B t !det(@J())
α =+0.57735, β =-0.57735
B = εuv @J4()^-1 @Form_uv()
K10= !dggr(B) D B t !det(@J())
α =+0.57735, β =+0.57735
B = εuv @J4()^-1 @Form_uv()
K11= !dggr(B) D B t !det(@J())
α =-0.57735, β =+0.57735
B = εuv @J4()^-1 @Form_uv()
K01= !dggr(B) D B t !det(@J())
Ktemp = K00 + K10 + K01 + K11
Ke=[[12]]
Ke[<0*12+0,8,1>]=Ktemp[0,*]
Ke[<1*12+0,8,1>]=Ktemp[1,*]
Ke[<2*12+0,8,1>]=Ktemp[2,*]
Ke[<3*12+0,8,1>]=Ktemp[3,*]
Ke[<4*12+0,8,1>]=Ktemp[4,*]
Ke[<5*12+0,8,1>]=Ktemp[5,*]
Ke[<6*12+0,8,1>]=Ktemp[6,*]
Ke[<7*12+0,8,1>]=Ktemp[7,*]
#add 1, 2 node
Ke[<2*12+2,2,1>]=Ke[<2*12+2,2,1>]+Ktemp[<0*8+0,2,1>], Ke[<2*12+4,2,1>]=Ke[<2*12+4,2,1>]+Ktemp[<0*8+6,2,1>]
Ke[<2*12+8,4,1>]=Ke[<2*12+8,4,1>]+Ktemp[<0*8+2,4,1>],
Ke[<3*12+2,2,1>]=Ke[<3*12+2,2,1>]+Ktemp[<1*8+0,2,1>], Ke[<3*12+4,2,1>]=Ke[<3*12+4,2,1>]+Ktemp[<1*8+6,2,1>]
Ke[<3*12+8,4,1>]=Ke[<3*12+8,4,1>]+Ktemp[<1*8+2,4,1>],
Ke[<4*12+2,2,1>]=Ke[<4*12+2,2,1>]+Ktemp[<6*8+0,2,1>], Ke[<4*12+4,2,1>]=Ke[<4*12+4,2,1>]+Ktemp[<6*8+6,2,1>]
Ke[<4*12+8,4,1>]=Ke[<4*12+8,4,1>]+Ktemp[<6*8+2,4,1>],
Ke[<5*12+2,2,1>]=Ke[<5*12+2,2,1>]+Ktemp[<7*8+0,2,1>], Ke[<5*12+4,2,1>]=Ke[<5*12+4,2,1>]+Ktemp[<7*8+6,2,1>]
Ke[<5*12+8,4,1>]=Ke[<5*12+8,4,1>]+Ktemp[<7*8+2,4,1>],
#add 4, 5 node
Ke[<8*12+2,2,1>]=Ktemp[<2*8+0,2,1>], Ke[<8*12+4,2,1>]=Ktemp[<2*8+6,2,1>], Ke[<8*12+8,4,1>]=Ktemp[<2*8+2,4,1>]
Ke[<9*12+2,2,1>]=Ktemp[<3*8+0,2,1>], Ke[<9*12+4,2,1>]=Ktemp[<3*8+6,2,1>], Ke[<9*12+8,4,1>]=Ktemp[<3*8+2,4,1>]
Ke[<10*12+2,2,1>]=Ktemp[<4*8+0,2,1>], Ke[<10*12+4,2,1>]=Ktemp[<4*8+6,2,1>], Ke[<10*12+8,4,1>]=Ktemp[<4*8+2,4,1>]
Ke[<11*12+2,2,1>]=Ktemp[<5*8+0,2,1>], Ke[<11*12+4,2,1>]=Ktemp[<5*8+6,2,1>], Ke[<11*12+8,4,1>]=Ktemp[<5*8+2,4,1>]
//@@@
計算された剛性行列は下の様になります
sf "/zs 1e-11, Ke"
< 10384.6, 3750, -6346.15, -288.462, -5192.31, -3750, 1153.85, 288.462, 0, 0, 0, 0 >
< 3750, 10384.6, 288.462, 1153.85, -3750, -5192.31, -288.462, -6346.15, 0, 0, 0, 0 >
< -6346.15, 288.462, 20769.2, 0, 2307.7, 0, -5192.31, 3750, -6346.15, -288.462, -5192.31, -3750 >
< -288.462, 1153.85, 0, 20769.2, 0, -12692.3, 3750, -5192.31, 288.462, 1153.85, -3750, -5192.31 >
< -5192.31, -3750, 2307.7, 0, 20769.2, 0, -6346.15, -288.462, -5192.31, 3750, -6346.15, 288.462 >
< -3750, -5192.31, 0, -12692.3, 0, 20769.2, 288.462, 1153.85, 3750, -5192.31, -288.462, 1153.85 >
< 1153.85, -288.462, -5192.31, 3750, -6346.15, 288.462, 10384.6, -3750, 0, 0, 0, 0 >
< 288.462, -6346.15, 3750, -5192.31, -288.462, 1153.85, -3750, 10384.6, 0, 0, 0, 0 >
< 0, 0, -6346.15, 288.462, -5192.31, 3750, 0, 0, 10384.6, -3750, 1153.85, -288.462 >
< 0, 0, -288.462, 1153.85, 3750, -5192.31, 0, 0, -3750, 10384.6, 288.462, -6346.15 >
< 0, 0, -5192.31, -3750, -6346.15, -288.462, 0, 0, 1153.85, 288.462, 10384.6, 3750 >
< 0, 0, -3750, -5192.31, 288.462, 1153.85, 0, 0, -288.462, -6346.15, 3750, 10384.6 >
Jacobi Ke
< -8.95956e-012, -5.92362e-012, -4.07602e-013, 3531.1, 9796.23, 11277.1
,13295.4, 14906.8, 17815, 20453.6, 36439.3, 38639.1 >
頂点 0, 3 を固定した剛性行列 K を作ります
//@@
K=Ke
e=<1,0,0,0, 0,0,0,0, 0,0,0,0>
K[0,*]=e
K[*,0]=e
K[1,*]=~shift(e,1*1)
K[*,1]=~shift(e,1*1)
K[3*2,*]=~shift(e,3*2)
K[*,3*2]=~shift(e,3*2)
K[3*2+1,*]=~shift(e,3*2+1)
K[*,3*2+1]=~shift(e,3*2+1)
//@@@
< 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 >
< 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 >
< 0, 0, 20769.2, 0, 2307.7, 0, 0, 0, -6346.15, -288.462, -5192.31, -3750 >
< 0, 0, 0, 20769.2, 0, -12692.3, 0, 0, 288.462, 1153.85, -3750, -5192.31 >
< 0, 0, 2307.7, 0, 20769.2, 0, 0, 0, -5192.31, 3750, -6346.15, 288.462 >
< 0, 0, 0, -12692.3, 0, 20769.2, 0, 0, 3750, -5192.31, -288.462, 1153.85 >
< 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0 >
< 0, 0, -6346.15, 288.462, -5192.31, 3750, 0, 0, 10384.6, -3750, 1153.85, -288.462 >
< 0, 0, -288.462, 1153.85, 3750, -5192.31, 0, 0, -3750, 10384.6, 288.462, -6346.15 >
< 0, 0, -5192.31, -3750, -6346.15, -288.462, 0, 0, 1153.85, 288.462, 10384.6, 3750 >
< 0, 0, -3750, -5192.31, 288.462, 1153.85, 0, 0, -288.462, -6346.15, 3750, 10384.6 >
4 の位置に 2000kgf の力を下向きに加えたときの変移:displacement と、力:force を計算します。
displacement = K^-1<0,0,0,0,0,0,0,0, -2000,0, 0,0>
< 0, 0, -0.284314, -0.209441, 0.100872, -0.175745
, 0, 0, -0.572654, -0.78379, 0.197718, -0.756952 >
/zs 1e-10, force = Ke displacement
< 2000, 210.575, 0, 0, 0, 0
, 0, -210.575, -2000, 0, 0, 0 >
Node 1, 2 の位置に加わる力は打ち消しあって 0 になっています。物理の理論どおりです。この計算も正しいと思われます。
2 N /cm^2 の圧力
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
|6 13 20 27 34 41 48 55 62 69 76 83 90 97 104 111 118 125 132 139 146
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+3cm
| M:5 | M:11 | M:17 | M:23 | M:29 | M:35 | M:41 | M:47 | M:53 | M:59 | M:65 | M:71 | M:77 | M:83 | M:89 | M:95 | M:101| M:107| M:113| M:119|
|5 12| 19| 26| 33| 40| 47| 54| 61| 68| 75| 82| 89| 96| 103| 110| 117| 124| 131| 138| 145|
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+2.5cm
| M:4 | M:10 | M:16 | M:22 | M:28 | M:34 | M:40 | M:46 | M:52 | M:58 | M:64 | M:70 | M:76 | M:82 | M:88 | M:94 | M:100| M:106| M:112| M:118|
|4 11| 18| 25| 32| 39| 46| 53| 60| 67| 74| 81| 88| 95| 102| 109| 116| 123| 130| 137| 144|
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+2cm
| M:3 | M:9 | M:15 | M:21 | M:27 | M:33 | M:39 | M:45 | M:51 | M:57 | M:63 | M:69 | M:75 | M:81 | M:87 | M:93 | M:99 | M:105| M:111| M:117|
|3 10| 17| 24| 31| 38| 45| 52| 59| 66| 73| 80| 87| 94| 101| 108| 115| 122| 129| 136| 143|
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+1.5cm
| M:2 | M:8 | M:14 | M:20 | M:26 | M:31 | M:38 | M:44 | M:50 | M:55 | M:62 | M:68 | M:74 | M:80 | M:86 | M:92 | M:98 | M:104| M:110| M:116|
|2 9| 16| 23| 30| 37| 44| 51| 58| 65| 72| 79| 86| 93| 100| 107| 114| 121| 128| 135| 142|
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+1cm
| M:1 | M:7 | M:13 | M:19 | M:25 | M:31 | M:37 | M:43 | M:49e| M:55 | M:61 | M:67 | M:73 | M:79 | M:85 | M:91 | M:97 | M:103| M:109| M:115|
|1 8| 15| 22| 29| 36| 43| 50| 57| 64| 71| 78| 85| 92| 99| 106| 113| 120| 127| 134| 141|
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+0.5cm
| M:0 | M:6 | M:12 | M:18 | M:24 | M:30 | M:36 | M:42 | M:48 | M:54 | M:60 | M:66 | M:72 | M:78 | M:84 | M:90 | M:96 | M:102| M:108| M:114|
|0 7| 14| 21| 28| 35| 42| 49| 56| 63| 70| 77| 84| 91| 98| 105| 112| 119| 126| 133| 140|
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+
| 0cm 0.5cm 1cm 1.5cm 2cm 2.5cm 3cm 3.5cm 4cm 4.5cm 5cm 5.5cm 6cm 6.5cm 7cm 7.5cm 8cm 8.5cm 9cm 9.5cm 100cm
t=1cm, E=300000 N/cm^2, Poisson ratio=0.2
下に Node 行列、 Mesh 行列の具体的な値を示します。
//@@
Node{0} =<0, 0>,Node{1} =<0, 0.5>,Node{2} =<0, 1.0>,Node{3} =<0, 1.5>,Node{4} =<0, 2.0>,Node{5} =<0, 2.5>,Node{6} =<0, 3.0>
Node{7} =<0.5, 0>,Node{8} =<0.5, 0.5>,Node{9} =<0.5, 1.0>,Node{10}=<0.5, 1.5>,Node{11}=<0.5, 2.0>,Node{12}=<0.5, 2.5>,Node{13}=<0.5, 3.0>
Node{14}=<1.0, 0>,Node{15}=<1.0, 0.5>,Node{16}=<1.0, 1.0>,Node{17}=<1.0, 1.5>,Node{18}=<1.0, 2.0>,Node{19}=<1.0, 2.5>,Node{20}=<1.0, 3.0>
Node{21}=<1.5, 0>,Node{22}=<1.5, 0.5>,Node{23}=<1.5, 1.0>,Node{24}=<1.5, 1.5>,Node{25}=<1.5, 2.0>,Node{26}=<1.5, 2.5>,Node{27}=<1.5, 3.0>
Node{28}=<2.0, 0>,Node{29}=<2.0, 0.5>,Node{30}=<2.0, 1.0>,Node{31}=<2.0, 1.5>,Node{32}=<2.0, 2.0>,Node{33}=<2.0, 2.5>,Node{34}=<2.0, 3.0>
Node{35}=<2.5, 0>,Node{36}=<2.5, 0.5>,Node{37}=<2.5, 1.0>,Node{38}=<2.5, 1.5>,Node{39}=<2.5, 2.0>,Node{40}=<2.5, 2.5>,Node{41}=<2.5, 3.0>
Node{42}=<3.0, 0>,Node{43}=<3.0, 0.5>,Node{44}=<3.0, 1.0>,Node{45}=<3.0, 1.5>,Node{46}=<3.0, 2.0>,Node{47}=<3.0, 2.5>,Node{48}=<3.0, 3.0>
Node{49}=<3.5, 0>,Node{50}=<3.5, 0.5>,Node{51}=<3.5, 1.0>,Node{52}=<3.5, 1.5>,Node{53}=<3.5, 2.0>,Node{54}=<3.5, 2.5>,Node{55}=<3.5, 3.0>
Node{56}=<4.0, 0>,Node{57}=<4.0, 0.5>,Node{58}=<4.0, 1.0>,Node{59}=<4.0, 1.5>,Node{60}=<4.0, 2.0>,Node{61}=<4.0, 2.5>,Node{62}=<4.0, 3.0>
Node{63}=<4.5, 0>,Node{64}=<4.5, 0.5>,Node{65}=<4.5, 1.0>,Node{66}=<4.5, 1.5>,Node{67}=<4.5, 2.0>,Node{68}=<4.5, 2.5>,Node{69}=<4.5, 3.0>
Node{70}=<5.0, 0>,Node{71}=<5.0, 0.5>,Node{72}=<5.0, 1.0>,Node{73}=<5.0, 1.5>,Node{74}=<5.0, 2.0>,Node{75}=<5.0, 2.5>,Node{76}=<5.0, 3.0>
Node{77}=<5.5, 0>,Node{78}=<5.5, 0.5>,Node{79}=<5.5, 1.0>,Node{80}=<5.5, 1.5>,Node{81}=<5.5, 2.0>,Node{82}=<5.5, 2.5>,Node{83}=<5.5, 3.0>
Node{84}=<6.0, 0>,Node{85}=<6.0, 0.5>,Node{86}=<6.0, 1.0>,Node{87}=<6.0, 1.5>,Node{88}=<6.0, 2.0>,Node{89}=<6.0, 2.5>,Node{90}=<6.0, 3.0>
Node{91}=<6.5, 0>,Node{92}=<6.5, 0.5>,Node{93}=<6.5, 1.0>,Node{94}=<6.5, 1.5>,Node{95}=<6.5, 2.0>,Node{96}=<6.5, 2.5>,Node{97}=<6.5, 3.0>
Node{98} =<7.0, 0>,Node{99} =<7.0, 0.5>,Node{100}=<7.0, 1.0>,Node{101}=<7.0, 1.5>,Node{102}=<7.0, 2.0>,Node{103}=<7.0, 2.5>,Node{104}=<7.0, 3.0>
Node{105}=<7.5, 0>,Node{106}=<7.5, 0.5>,Node{107}=<7.5, 1.0>,Node{108}=<7.5, 1.5>,Node{109}=<7.5, 2.0>,Node{110}=<7.5, 2.5>,Node{111}=<7.5, 3.0>
Node{112}=<8.0, 0>,Node{113}=<8.0, 0.5>,Node{114}=<8.0, 1.0>,Node{115}=<8.0, 1.5>,Node{116}=<8.0, 2.0>,Node{117}=<8.0, 2.5>,Node{118}=<8.0, 3.0>
Node{119}=<8.5, 0>,Node{120}=<8.5, 0.5>,Node{121}=<8.5, 1.0>,Node{122}=<8.5, 1.5>,Node{123}=<8.5, 2.0>,Node{124}=<8.5, 2.5>,Node{125}=<8.5, 3.0>
Node{126}=<9.0, 0>,Node{127}=<9.0, 0.5>,Node{128}=<9.0, 1.0>,Node{129}=<9.0, 1.5>,Node{130}=<9.0, 2.0>,Node{131}=<9.0, 2.5>,Node{132}=<9.0, 3.0>
Node{133}=<9.5, 0>,Node{134}=<9.5, 0.5>,Node{135}=<9.5, 1.0>,Node{136}=<9.5, 1.5>,Node{137}=<9.5, 2.0>,Node{138}=<9.5, 2.5>,Node{139}=<9.5, 3.0>
Node{140}=<10, 0>,Node{141}=<10, 0.5>,Node{142}=<10, 1.0>,Node{143}=<10, 1.5>,Node{144}=<10, 2.0>,Node{145}=<10, 2.5>,Node{146}=<10, 3.0>
MeshTemp = [[120,4]]
MeshTemp[0,*]=<0,7,8,1>,MeshTemp[1,*]=<1,8,9,2>,MeshTemp[2,*]=<2,9,10,3>,MeshTemp[3,*]=<3,10,11,4>,MeshTemp[4,*]=<4,11,12,5>,MeshTemp[5,*]=<5,12,13,6>
MeshTemp[6,*]=<7,14,15,8>,MeshTemp[7,*]=<8,15,16,9>,MeshTemp[8,*]=<9,16,17,10>,MeshTemp[9,*]=<10,17,18,11>,MeshTemp[10,*]=<11,18,19,12>,MeshTemp[11,*]=<12,19,20,13>
MeshTemp[12,*]=<14,21,22,15>,MeshTemp[13,*]=<15,22,23,16>,MeshTemp[14,*]=<16,23,24,17>,MeshTemp[15,*]=<17,24,25,18>,MeshTemp[16,*]=<18,25,26,19>,MeshTemp[17,*]=<19,26,27,20>
MeshTemp[18,*]=<21,28,29,22>,MeshTemp[19,*]=<22,29,30,23>,MeshTemp[20,*]=<23,30,31,24>,MeshTemp[21,*]=<24,31,32,25>,MeshTemp[22,*]=<25,32,33,26>,MeshTemp[23,*]=<26,33,34,27>
MeshTemp[24,*]=<28,35,36,29>,MeshTemp[25,*]=<29,36,37,30>,MeshTemp[26,*]=<30,37,38,31>,MeshTemp[27,*]=<31,38,39,32>,MeshTemp[28,*]=<32,39,40,33>,MeshTemp[29,*]=<33,40,41,34>
MeshTemp[30,*]=<35,42,43,36>,MeshTemp[31,*]=<36,43,44,37>,MeshTemp[32,*]=<37,44,45,38>,MeshTemp[33,*]=<38,45,46,39>,MeshTemp[34,*]=<39,46,47,40>,MeshTemp[35,*]=<40,47,48,41>
MeshTemp[36,*]=<42,49,50,43>,MeshTemp[37,*]=<43,50,51,44>,MeshTemp[38,*]=<44,51,52,45>,MeshTemp[39,*]=<45,52,53,46>,MeshTemp[40,*]=<46,53,54,47>,MeshTemp[41,*]=<47,54,55,48>
MeshTemp[42,*]=<49,56,57,50>,MeshTemp[43,*]=<50,57,58,51>,MeshTemp[44,*]=<51,58,59,52>,MeshTemp[45,*]=<52,59,60,53>,MeshTemp[46,*]=<53,60,61,54>,MeshTemp[47,*]=<54,61,62,55>
MeshTemp[48,*]=<56,63,64,57>,MeshTemp[49,*]=<57,64,65,58>,MeshTemp[50,*]=<58,65,66,59>,MeshTemp[51,*]=<59,66,67,60>,MeshTemp[52,*]=<60,67,68,61>,MeshTemp[53,*]=<61,68,69,62>
MeshTemp[54,*]=<63,70,71,64>,MeshTemp[55,*]=<64,71,72,65>,MeshTemp[56,*]=<65,72,73,66>,MeshTemp[57,*]=<66,73,74,67>,MeshTemp[58,*]=<67,74,75,68>,MeshTemp[59,*]=<68,75,76,69>
MeshTemp[60,*]=<70,77,78,71>,MeshTemp[61,*]=<71,78,79,72>,MeshTemp[62,*]=<72,79,80,73>,MeshTemp[63,*]=<73,80,81,74>,MeshTemp[64,*]=<74,81,82,75>,MeshTemp[65,*]=<75,82,83,76>
MeshTemp[66,*]=<77,84,85,78>,MeshTemp[67,*]=<78,85,86,79>,MeshTemp[68,*]=<79,86,87,80>,MeshTemp[69,*]=<80,87,88,81>,MeshTemp[70,*]=<81,88,89,82>,MeshTemp[71,*]=<82,89,90,83>
MeshTemp[72,*]=<84,91,92,85>,MeshTemp[73,*]=<85,92,93,86>,MeshTemp[74,*]=<86,93,94,87>,MeshTemp[75,*]=<87,94,95,88>,MeshTemp[76,*]=<88,95,96,89>,MeshTemp[77,*]=<89,96,97,90>
MeshTemp[78,*]=< 91,98, 99, 92>,MeshTemp[79,*]=< 92,99, 100, 93>,MeshTemp[80,*]=< 93,100,101, 94>,MeshTemp[81,*]=< 94,101,102, 95>,MeshTemp[82,*]=< 95,102,103, 96>,MeshTemp[83,*]=< 96,103,104, 97>
MeshTemp[84,*]=< 98,105,106, 99>,MeshTemp[85,*]=< 99,106,107,100>,MeshTemp[86,*]=<100,107,108,101>,MeshTemp[87,*]=<101,108,109,102>,MeshTemp[88,*]=<102,109,110,103>,MeshTemp[89,*]=<103,110,111,104>
MeshTemp[90,*]=<105,112,113,106>,MeshTemp[91,*]=<106,113,114,107>,MeshTemp[92,*]=<107,114,115,108>,MeshTemp[93,*]=<108,115,116,109>,MeshTemp[94,*]=<109,116,117,110>,MeshTemp[95,*]=<110,117,118,111>
MeshTemp[ 96,*]=<112,119,120,113>,MeshTemp[ 97,*]=<113,120,121,114>,MeshTemp[ 98,*]=<114,121,122,115>,MeshTemp[ 99,*]=<115,122,123,116>,MeshTemp[100,*]=<116,123,124,117>,MeshTemp[101,*]=<117,124,125,118>
MeshTemp[102,*]=<119,126,127,120>,MeshTemp[103,*]=<120,127,128,121>,MeshTemp[104,*]=<121,128,129,122>,MeshTemp[105,*]=<122,129,130,123>,MeshTemp[106,*]=<123,130,131,124>,MeshTemp[107,*]=<124,131,132,125>
MeshTemp[108,*]=<126,133,134,127>,MeshTemp[109,*]=<127,134,135,128>,MeshTemp[110,*]=<128,135,136,129>,MeshTemp[111,*]=<129,136,137,130>,MeshTemp[112,*]=<130,137,138,131>,MeshTemp[113,*]=<131,138,139,132>
MeshTemp[114,*]=<133,140,141,134>,MeshTemp[115,*]=<134,141,142,135>,MeshTemp[116,*]=<135,142,143,136>,MeshTemp[117,*]=<136,143,144,137>,MeshTemp[118,*]=<137,144,145,138>,MeshTemp[119,*]=<138,145,146,139>
Mesh = MeshTemp
//@@@
Mesh/Node での計算がしやすいように、 sf サブルーチン・ファイルも下のように修正します。
//@@
@@subFile makeK #(α,β) 引数
α@= _prm{1}
β@= _prm{2}
J=[[2]]
J[0,*] = <(-(1-β)Node{p}[0] + (1-β)Node{q}[0] + (1+β)Node{r}[0] - (1+β)Node{s}[0])/4
(-(1-β)Node{p}[1] + (1-β)Node{q}[1] + (1+β)Node{r}[1] - (1+β)Node{s}[1])/4>
J[1,*] = <(-(1-α)Node{p}[0] - (1+α)Node{q}[0] + (1+α)Node{r}[0] + (1-α)Node{s}[0])/4
(-(1-α)Node{p}[1] - (1+α)Node{q}[1] + (1+α)Node{r}[1] + (1-α)Node{s}[1])/4>
J4 = [[4]]
J4[<0+0*4,2,1>]=J[0,*]
J4[<0+1*4,2,1>]=J[1,*]
J4[<2+2*4,2,1>]=J[0,*]
J4[<2+3*4,2,1>]=J[1,*]
Form_uv @=[[4,8]]
Form_uv[0,*]=< -(1-β)/4, 0, (1-β)/4, 0, (1+β)/4, 0, -(1+β)/4, 0 >
Form_uv[1,*]=< 0, -(1-β)/4, 0, (1-β)/4, 0, (1+β)/4, 0, -(1+β)/4>
Form_uv[2,*]=< -(1-α)/4, 0,-(1+α)/4, 0, (1+α)/4, 0, (1-α)/4, 0 >
Form_uv[3,*]=< 0, -(1-α)/4, 0,-(1+α)/4, 0, (1+α)/4, 0, (1-α)/4>
B @= εuv J4^-1 Form_uv
_rt = !dggr(B) D B t !det(J)
@@endSubFile
@@subFile SetKatKe
_rt=0
Ke[< 2 p N + 2 p, 2, 1>] = Ke[< 2 p N + 2 p, 2, 1>] +K[<0*8+0*2,2,1>]
Ke[< 2 p N + 2 q, 2, 1>] = Ke[< 2 p N + 2 q, 2, 1>] +K[<0*8+1*2,2,1>]
Ke[< 2 p N + 2 r, 2, 1>] = Ke[< 2 p N + 2 r, 2, 1>] +K[<0*8+2*2,2,1>]
Ke[< 2 p N + 2 s, 2, 1>] = Ke[< 2 p N + 2 s, 2, 1>] +K[<0*8+3*2,2,1>]
Ke[<(2 p+1) N + 2 p, 2, 1>] = Ke[<(2 p+1) N + 2 p, 2, 1>]+K[<1*8+0*2,2,1>]
Ke[<(2 p+1) N + 2 q, 2, 1>] = Ke[<(2 p+1) N + 2 q, 2, 1>]+K[<1*8+1*2,2,1>]
Ke[<(2 p+1) N + 2 r, 2, 1>] = Ke[<(2 p+1) N + 2 r, 2, 1>]+K[<1*8+2*2,2,1>]
Ke[<(2 p+1) N + 2 s, 2, 1>] = Ke[<(2 p+1) N + 2 s, 2, 1>]+K[<1*8+3*2,2,1>]
Ke[< 2 q N + 2 p, 2, 1>] = Ke[< 2 q N + 2 p, 2, 1>] +K[<2*8+0*2,2,1>]
Ke[< 2 q N + 2 q, 2, 1>] = Ke[< 2 q N + 2 q, 2, 1>] +K[<2*8+1*2,2,1>]
Ke[< 2 q N + 2 r, 2, 1>] = Ke[< 2 q N + 2 r, 2, 1>] +K[<2*8+2*2,2,1>]
Ke[< 2 q N + 2 s, 2, 1>] = Ke[< 2 q N + 2 s, 2, 1>] +K[<2*8+3*2,2,1>]
Ke[<(2 q+1) N + 2 p, 2, 1>] = Ke[<(2 q+1) N + 2 p, 2, 1>]+K[<3*8+0*2,2,1>]
Ke[<(2 q+1) N + 2 q, 2, 1>] = Ke[<(2 q+1) N + 2 q, 2, 1>]+K[<3*8+1*2,2,1>]
Ke[<(2 q+1) N + 2 r, 2, 1>] = Ke[<(2 q+1) N + 2 r, 2, 1>]+K[<3*8+2*2,2,1>]
Ke[<(2 q+1) N + 2 s, 2, 1>] = Ke[<(2 q+1) N + 2 s, 2, 1>]+K[<3*8+3*2,2,1>]
Ke[< 2 r N + 2 p, 2, 1>] = Ke[< 2 r N + 2 p, 2, 1>] +K[<4*8+0*2,2,1>]
Ke[< 2 r N + 2 q, 2, 1>] = Ke[< 2 r N + 2 q, 2, 1>] +K[<4*8+1*2,2,1>]
Ke[< 2 r N + 2 r, 2, 1>] = Ke[< 2 r N + 2 r, 2, 1>] +K[<4*8+2*2,2,1>]
Ke[< 2 r N + 2 s, 2, 1>] = Ke[< 2 r N + 2 s, 2, 1>] +K[<4*8+3*2,2,1>]
Ke[<(2 r+1) N + 2 p, 2, 1>] = Ke[<(2 r+1) N + 2 p, 2, 1>]+K[<5*8+0*2,2,1>]
Ke[<(2 r+1) N + 2 q, 2, 1>] = Ke[<(2 r+1) N + 2 q, 2, 1>]+K[<5*8+1*2,2,1>]
Ke[<(2 r+1) N + 2 r, 2, 1>] = Ke[<(2 r+1) N + 2 r, 2, 1>]+K[<5*8+2*2,2,1>]
Ke[<(2 r+1) N + 2 s, 2, 1>] = Ke[<(2 r+1) N + 2 s, 2, 1>]+K[<5*8+3*2,2,1>]
Ke[< 2 s N + 2 p, 2, 1>] = Ke[< 2 s N + 2 p, 2, 1>] +K[<6*8+0*2,2,1>]
Ke[< 2 s N + 2 q, 2, 1>] = Ke[< 2 s N + 2 q, 2, 1>] +K[<6*8+1*2,2,1>]
Ke[< 2 s N + 2 r, 2, 1>] = Ke[< 2 s N + 2 r, 2, 1>] +K[<6*8+2*2,2,1>]
Ke[< 2 s N + 2 s, 2, 1>] = Ke[< 2 s N + 2 s, 2, 1>] +K[<6*8+3*2,2,1>]
Ke[<(2 s+1) N + 2 p, 2, 1>] = Ke[<(2 s+1) N + 2 p, 2, 1>]+K[<7*8+0*2,2,1>]
Ke[<(2 s+1) N + 2 q, 2, 1>] = Ke[<(2 s+1) N + 2 q, 2, 1>]+K[<7*8+1*2,2,1>]
Ke[<(2 s+1) N + 2 r, 2, 1>] = Ke[<(2 s+1) N + 2 r, 2, 1>]+K[<7*8+2*2,2,1>]
Ke[<(2 s+1) N + 2 s, 2, 1>] = Ke[<(2 s+1) N + 2 s, 2, 1>]+K[<7*8+3*2,2,1>]
@@endSubFile
//@@@
後は、上の Mesh/Node データを読み出しながら、上のサブルーチン・ファイル働かせて、要素剛性行列を計算し、全体剛性行列に足し合わせていきます。私の Athron 1800+ では 12 分程度かかりました。しばらくお待ちください。
//@@
/s
p@ ,q@ ,r@ ,s@
εuv @=[[ 3,4]]
εuv[0,*]=<1,0,0,0>
εuv[1,*]=<0,0,0,1>
εuv[2,*]=<0,1,1,0>
NN@=20
N@ = 7*(NN+1)*2
Ke @= [[N]] # temporary 変数にしておかないと何時間もの計算時間になってしまう
t@=1 # 板厚 1cm
E @= 300000 # Young 率
μ @= 0.2 # Poisson 比
D=[[3]]
D[0,*]=<1,μ, 0> E/(1-μ^2)
D[1,*]=<μ,1, 0> E/(1-μ^2)
D[2,*]=<0,0,(1-μ)/2> E/(1-μ^2)
<<0,6*NN,1@j|\
dbgJ = j # save debug Indeex in dbgJ.val file
p=Mesh[j,0],q=Mesh[j,1],r=Mesh[j,2],s=Mesh[j,3]
K = @makeK(-0.57735, -0.57735) + @makeK(+0.57735, -0.57735) + @makeK(-0.57735, +0.57735) + @makeK(+0.57735, +0.57735)
@SetKatKe()
>>
Ke{6*NN} = Ke
//@@@
Jacobi Ke{120}
< -1.4038e-010, 1.20301e-011, 1.4575e-010, 1245.34, 5675.14, 5710.46, 13912, 21699
, 23074.3, 27040, 28314.7, 31835.4, 34191.2, 46370.5, 48161.6, 50826.7
, 54232.9, 54782, 55236.2, 58779.7, 59404.6, 62073.9, 70836.4, 72195.9
, 72275.1, 85858.2, 85896, 87674.5, 96731.1, 98600.6, 102067, 103128
, 107890, 117027, 117238, 128525, 128557, 128931, 135684, 139085
, 147742, 153620, 156034, 162441, 164804, 166188, 169208, 169672
, 170721, 174975, 179717, 182119, 182563, 189383, 190212, 190286
, 193898, 200579, 203184, 203715, 210195, 210475, 213327, 220909
, 225324, 225779, 228925, 229043, 231148, 238241, 239826, 240028
, 242032, 244290, 251607, 253625, 256777, 258509, 259751, 261657
, 263270, 263709, 265319, 267391, 267903, 268587, 270010, 271231
, 276332, 279569, 279588, 289434, 290418, 296392, 301527, 302769
, 306001, 307474, 310910, 315765, 317834, 320119, 322708, 324055
, 324172, 332259, 333282, 336986, 340818, 341136, 342675, 348340
, 350584, 354793, 355028, 357063, 361234, 363090, 363952, 367771
, 367800, 370965, 373630, 378086, 379355, 380182, 384067, 385039
, 386772, 387757, 390999, 391979, 394910, 396682, 400988, 401107
, 403556, 405960, 406768, 409501, 412239, 414992, 415831, 416605
, 422446, 424559, 427681, 430184, 432094, 439577, 443316, 445113
, 448885, 457830, 465245, 465728, 468371, 470905, 474950, 475349
, 476931, 480064, 483155, 484053, 484549, 485845, 488465, 490144
, 494364, 495014, 496206, 497009, 498309, 500131, 503277, 505792
, 507656, 509388, 509885, 512097, 514061, 518678, 519472, 520631
, 520976, 526348, 530114, 534059, 536678, 537208, 541230, 541412
, 547696, 553198, 554275, 555170, 557623, 560782, 562644, 577525
, 582213, 584602, 594665, 603123, 607915, 614301, 629330, 635600
, 637288, 639234, 649256, 654690, 656911, 660119, 662563, 668712
, 672257, 673118, 686357, 686994, 697529, 701562, 702632, 706516
, 711061, 713399, 718906, 755391, 755607, 757384, 757475, 759408
, 760878, 762523, 763525, 764337, 764787, 765306, 768275, 778881
, 779669, 782313, 784800, 785163, 785875, 785903, 786751, 790459
, 820226, 822785, 829016, 829468, 841827, 846141, 855291, 860334
, 865589, 882145, 883007, 890569, 903967, 906572, 915546, 922734
, 926781, 936075, 939294, 941517, 948345, 950659, 960831, 979453
, 984673, 991824, 993740, 994608, 1.00562e+006, 1.0124e+006, 1.02671e+006, 1.03313e+006
, 1.05711e+006, 1.06074e+006, 1.0712e+006, 1.08574e+006, 1.10101e+006, 1.10511e+006, 1.11112e+006, 1.13404e+006
, 1.15452e+006, 1.15727e+006, 1.17427e+006, 1.18463e+006, 1.18627e+006, 1.20562e+006 >
全体の剛性行列の計算結果は表示するには多すぎるデータ量なので、表示しませんが、その固有値だけは上に示しておきます。ここでも三つの固有値が 0 になっており、計算結果は正しそうです。
Node 0,1,2,3,4,5,6,7 が固定されているときの剛性行列 K は下のように計算できます。
//@@
/s # これを入れないと計算のするたびにコンソールに KTemp 行列値全部を表示するので、時間がかかる。
KTemp@=Ke{120} # Ke{120} が大きいので temporary 変数を介さないと処理に時間がかかる
e1=<<(6+1)*(20+1)*2>>
e1[0]=1
#Node0,... Node 6 を固定して、対応する行列要素を 1 にします
KTemp[0,*] = e1
KTemp[*,0] = e1
KTemp[1,*] = ~shift(e1,1)
KTemp[*,1] = ~shift(e1,1)
# Node 1
KTemp[2,*] = ~shift(e1,2)
KTemp[*,2] = ~shift(e1,2)
KTemp[3,*] = ~shift(e1,3)
KTemp[*,3] = ~shift(e1,3)
# Node 2
KTemp[4,*] = ~shift(e1,4)
KTemp[*,4] = ~shift(e1,4)
KTemp[5,*] = ~shift(e1,5)
KTemp[*,5] = ~shift(e1,5)
# Node 3
KTemp[6,*] = ~shift(e1,6)
KTemp[*,6] = ~shift(e1,6)
KTemp[7,*] = ~shift(e1,7)
KTemp[*,7] = ~shift(e1,7)
# Node 4
KTemp[8,*] = ~shift(e1,8)
KTemp[*,8] = ~shift(e1,8)
KTemp[9,*] = ~shift(e1,9)
KTemp[*,9] = ~shift(e1,9)
# Node 5
KTemp[10,*] = ~shift(e1,10)
KTemp[*,10] = ~shift(e1,10)
KTemp[11,*] = ~shift(e1,11)
KTemp[*,11] = ~shift(e1,11)
# Node 6
KTemp[12,*] = ~shift(e1,12)
KTemp[*,12] = ~shift(e1,12)
KTemp[13,*] = ~shift(e1,13)
KTemp[*,13] = ~shift(e1,13)
K = KTemp
//@@@
梁の上面からかかる 2N/cm\2 の圧力:force は下のように記述できます。
//@@
force=<<(6+1)*(20+1)*2>>
#force[< 6*2,2,1>]=<0,-1> # Note 6 は y 方向にも固定されており、外力は固定によりキャンセルされます
force[< 13*2,2,1>]=<0,-2>
force[< 20*2,2,1>]=<0,-2>
force[< 27*2,2,1>]=<0,-2>
force[< 34*2,2,1>]=<0,-2>
force[< 41*2,2,1>]=<0,-2>
force[< 48*2,2,1>]=<0,-2>
force[< 55*2,2,1>]=<0,-2>
force[< 62*2,2,1>]=<0,-2>
force[< 69*2,2,1>]=<0,-2>
force[< 76*2,2,1>]=<0,-2>
force[< 83*2,2,1>]=<0,-2>
force[< 90*2,2,1>]=<0,-2>
force[< 97*2,2,1>]=<0,-2>
force[<104*2,2,1>]=<0,-2>
force[<111*2,2,1>]=<0,-2>
force[<118*2,2,1>]=<0,-2>
force[<125*2,2,1>]=<0,-2>
force[<132*2,2,1>]=<0,-2>
force[<139*2,2,1>]=<0,-2>
force[<146*2,2,1>]=<0,-1>
//@@@
圧力:force による変移:displacement は下のようになります。
displacement = K^-1 force
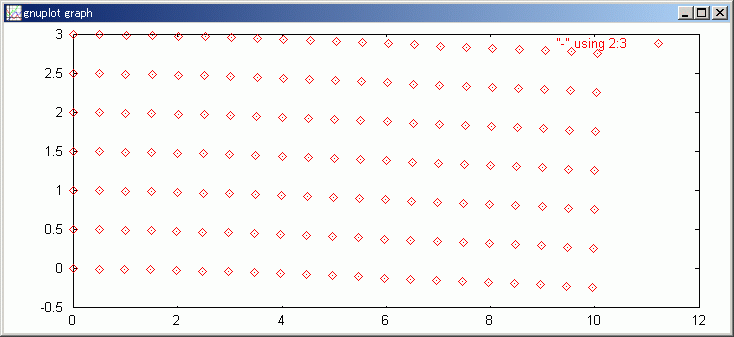
Node に displacement を足してやれば圧力による歪の具合がわかります。ただし、目視で解かりやすくするため、30 倍に拡大してやります。同時に gdspl.bat を使って gnuplot 表示させるために、displacement 実数ベクタを cplxDsplc 複素数ベクタ表示に変更します。
#変移距離を 30 倍に拡大して表示させる
M@=30, displayData = <<0,!size(displacement)/2,1@j| >>
#cplxDsplc データをgnuplot 向け表示データにする
gdsp displayData
# gnuplot.ini の行頭を plot "-" using 2:3 with line ==> plot "-" using 2:3
start wgnuplot
//@@
エディタを使って gnuplot.ini ファイルの 1 行目「plot "-" using 2:3 with line」 を「 plot "-" using 2:3」に変更し、"start \ap\gnuplot\wgnupl32.exe" を実行すれば、歪の様子を表示できます。
2 N /cm^2 の圧力
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
|6 13 20 27 34 41 48 55 62 69 76 83 90 97 104 111 118 125 132 139 146
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+3cm
| M:5 | M:11 | M:17 | M:23 | M:29 | M:35 | M:41 | M:47 | M:53 | M:59 | M:65 | M:71 | M:77 | M:83 | M:89 | M:95 | M:101| M:107| M:113| M:119|
|5 12| 19| 26| 33| 40| 47| 54| 61| 68| 75| 82| 89| 96| 103| 110| 117| 124| 131| 138| 145|
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+2.5cm
| M:4 | M:10 | M:16 | M:22 | M:28 | M:34 | M:40 | M:46 | M:52 | M:58 | M:64 | M:70 | M:76 | M:82 | M:88 | M:94 | M:100| M:106| M:112| M:118|
|4 11| 18| 25| 32| 39| 46| 53| 60| 67| 74| 81| 88| 95| 102| 109| 116| 123| 130| 137| 144|
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+2cm
| M:3 | M:9 | M:15 | M:21 | M:27 | M:33 | M:39 | M:45 | M:51 | M:57 | M:63 | M:69 | M:75 | M:81 | M:87 | M:93 | M:99 | M:105| M:111| M:117|
|3 10| 17| 24| 31| 38| 45| 52| 59| 66| 73| 80| 87| 94| 101| 108| 115| 122| 129| 136| 143|
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+1.5cm
| M:2 | M:8 | M:14 | M:20 | M:26 | M:31 | M:38 | M:44 | M:50 | M:55 | M:62 | M:68 | M:74 | M:80 | M:86 | M:92 | M:98 | M:104| M:110| M:116|
|2 9| 16| 23| 30| 37| 44| 51| 58| 65| 72| 79| 86| 93| 100| 107| 114| 121| 128| 135| 142|
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+1cm
| M:1 | M:7 | M:13 | M:19 | M:25 | M:31 | M:37 | M:43 | M:49e| M:55 | M:61 | M:67 | M:73 | M:79 | M:85 | M:91 | M:97 | M:103| M:109| M:115|
|1 8| 15| 22| 29| 36| 43| 50| 57| 64| 71| 78| 85| 92| 99| 106| 113| 120| 127| 134| 141|
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+0.5cm
| M:0 | M:6 | M:12 | M:18 | M:24 | M:30 | M:36 | M:42 | M:48 | M:54 | M:60 | M:66 | M:72 | M:78 | M:84 | M:90 | M:96 | M:102| M:108| M:114|
|0 7| 14| 21| 28| 35| 42| 49| 56| 63| 70| 77| 84| 91| 98| 105| 112| 119| 126| 133| 140|
|■------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+------+
| 0cm 0.5cm 1cm 1.5cm 2cm 2.5cm 3cm 3.5cm 4cm 4.5cm 5cm 5.5cm 6cm 6.5cm 7cm 7.5cm 8cm 8.5cm 9cm 9.5cm ◎ 100cm
ローラー指示を右下に追加
t=1cm, E=300000 N/cm^2, Poisson ratio=0.2
node 140 の x 軸を固定するだけであり、先に作った剛性行列 K で、対応する縦、横成分を下のように置き換えてやります。
//@@
/s
# Node 140
K[140*2+1,*] = ~shift(e1,140*2+1)
K[*,140*2+1] = ~shift(e1,140*2+1)
//@@@
加える圧力は先に作った force をそのまま使えます。gnuplot で表示するまでの手続きは前回と殆ど同じです。ただし、今回は歪かたが小さいので 300 倍に拡大して表示させます。
displacement = K^-1 force
#変移距離を 300 倍に拡大して表示させる
M@=300, displayData = <<0,!size(displacement)/2,1@j| >>
#cplxDsplc データを gnuplot 向け表示データにする
gdsp displayData
# gnuplot.ini の行頭を plot "-" using 2:3 with line ==> plot "-" using 2:3
start wgnuplot.exe
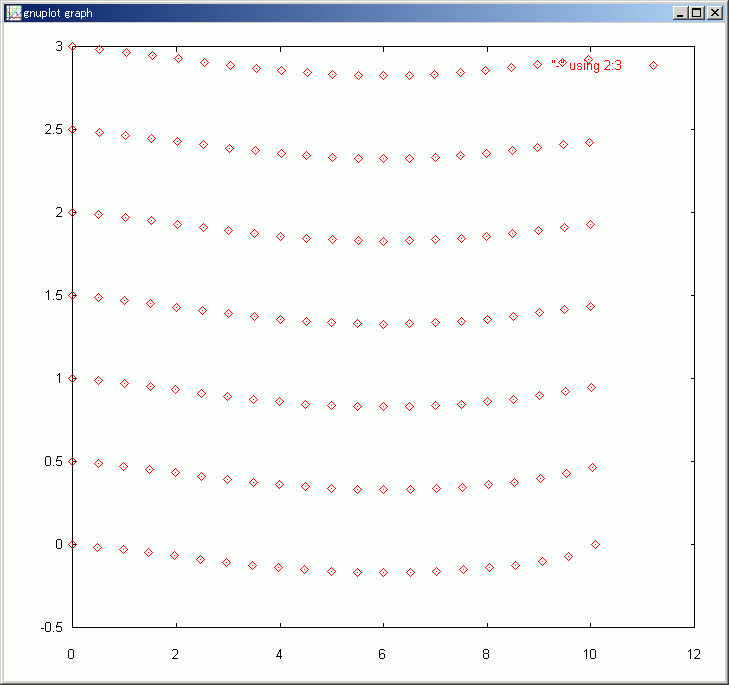
この程度の計算でも十分に実用的な実務分野も多くあるはずです。是非とも自分でも計算してみてください。