形状関数

１ 三角形要素 二次元形状関数

<x0,y0,0>, &;tx1,y1,0>, <x2,y2,0> 三点の温度分布 T0,T1,T2 を下の平面三角形 T0* N0(x,y)+T1*N1(x,y)+T2*N2(x,y) で近似します。
 

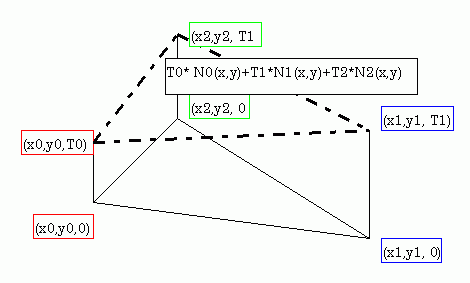
図１ 三角形要素による平面温度分布表示

N0(x,y) は下の三っつの頂点 (x0,y0,1), (x1,y1,0), (x2,y2,0) を結んでできる三角形平面です。


図２ 三角形要素 N0(x,y)
N1(x,y) は (x0,y0,0), (x1,y1,1), (x2,y2,0) を結んでできる三角形平面です。 画像を省略しますが N2(x,y) は (x0,y0,0), (x1,y1,0), (x2,y2,1) を結んでできる三角形平面です。
 

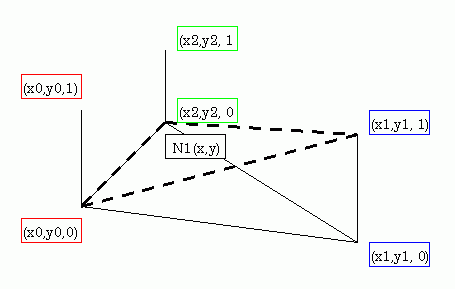
図３ 三角形要素 N1(x,y)

N0(x,y),N1(x,y),N2(x,y) の三角形で表される平面を下の式で表しておき (a0,b0,c0),(a1,b1,c1),(a2,b2,c2) を求めてみます。 

    N0(x,y) == a0 + b0 x + c0 y
    N1(x,y) == a1 + b1 x + c2 y
    N2(x,y) == a2 + b1 x + c2 y
N0(x,y),N1(x,y),Ny(x,y) は下の関係式を満たします。 
    N0(x,y) + N1(x,y) + N2(x,y)         == 1
    N0(x,y) x0 + N1(x,y) x1+ N2(x,y) x2 == x
    N0(x,y) y0 + N1(x,y) y1+ N2(x,y) y2 == y
上の関係は下の行列式と同値です。 
    │1   1   1 │  │ a0  b0  c0││1│  ==  │1│
    │x0  x1  x2│  │ a1  b1  c1││x│      │x│  for ∀x, ∀y ∈ Real Number
    │y0  y1  y2│  │ a2  b2  c2││y│      │y│
上の等式が全ての x,y についてなりたつのは下の行列式が成り立つことと同値です。すなわち、(a0,b0,c0),(a1,b1,c1),(a2,b2,c2) の要素から成り立つ a b c 行列は x y 行列の逆行列であることが言えます。すなわち (x0,y0), (x1,y1), (x2,y2) より N0(x,y), N1(x,y), N2(x,y) が定まります。 
    │1   1   1 │  │ a0  b0  c0│      │1   0   0 │
    │x0  x1  x2│  │ a1  b1  c1│ ==   │0   1   0 │
    │y0  y1  y2│  │ a2  b2  c2│      │0   0   1 │

      x y 行列         a b c 行列

この N0(x,y), N1(x,y), N2(x,y) に (x0,y0), (x1,y1), (x2,y2) での温度分布 (T0,T1,T2) を掛けて T0* N0(x,y)+T1*N1(x,y)+T2*N2(x,y) を作ってやれば、これは三点の温度分布を平面で近似したものになっています。

上の関係式が納得できない方は sf を使い、より詳細に御自分で計算をしてみてください。式だけを眺めているより深く理解できるはずです。



２ パラメトリック四角形要素

パラメトリック四角形要素は、二つのパラメーター ａ,b∈[0,1] によって四角形の四つの頂点の温度 T0, T1,T2,T3 によって四角形内の温度を下の式によって近似します。 
    1/4*((1- )*(1-b )*T0 + (1+a )*(1-b )*T1 + (1+a )*(1+b )*T2 + (1-a )*(1+b )*T3

    a∈[-1,1]  b∈[-1,1]
(T0,T1,T2,T3) == (1,2,3,4) のときのパラメトリック近似の様子を下に示します。平面ではないのですが、縦と横のグリッドは直線となる曲面です

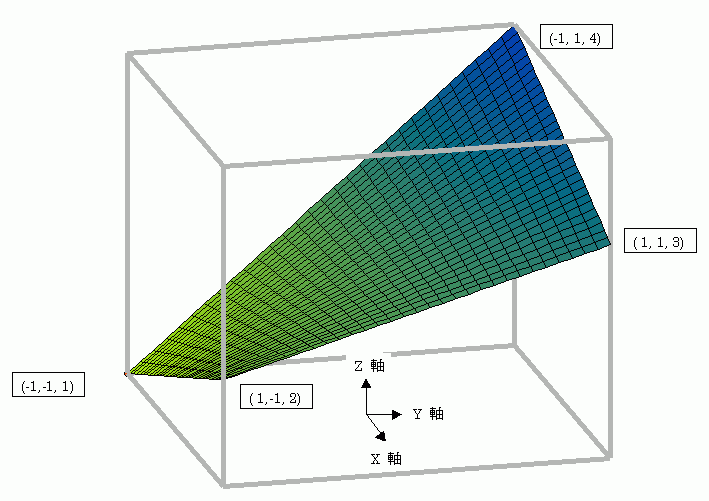
この曲面の三次元での様子が直感的にイメージできないときは Maxima や gnuplot などに是非とも自分で描かせて見てください。これらの三次元プロットはマウスで回転できますから曲面の曲がり具合が良くわかります。

下に Maxima でのプロット・コマンドを示しておきます。

    N0:1;
    N1:2;
    N2:3;
    N3:4;
    plot3d( 1/4*((1-a )*(1-b )*N0 + (1+a )*(1-b )*N1 + (1+a )*(1+b )*N2 + (1-a )*(1+b )*N3),[a,-1,1],[b,-1,1]);
ホーム ページに戻る