python sf は python の科学技術計算モジュールをワンライナーで利用できるようにしたプリプロセッサです。科学技術計算機能の多くは、scipy, simpy, visual などの既存 python モジュールによるものです。それらをワンライナーでも扱えるようにしたことで、数学ソフトの L.L.(Light weight Language) にできたと思います。Python sf を使えば、大部分のユーザーが より手軽な記述で、Mathematica, Matlab などの既存の数学ソフトの機能の多くを代換できます。多くのユーザーが手軽に使える Light Weight Language の意味でならば、Mathematica, Maple, Matlab などを超えている自負しています。
例えば python sf では ~[...] で行列、ベクトルを表せます。次のような、ワンライナーによる、行列・ベクトル演算が可能です。
行列の宣言;;mt=~[(1,2), (3,4)] =============================== [[ 1. 2.] [ 3. 4.]] 行列の多項式;;mt=~[(1,2), (3,4)]; (mt^2 + 2 mt + mt^-2) =============================== [[ 13. 15. ] [ 23.25 30.25]] 上の行列の 0 行目ベクトル;;mt:=~[(1,2), (3,4)]; (mt^2 + 2 mt + mt^-2)[0,:] =============================== [ 13. 15.]
前回の計算を残しておき再利用するために、「:=」で、カレント・ディレクトリに、その変数名のファイル(この場合は mt.pvl の名前のファイル)を作り記録します。「=:fileName」(この場合は =:mt)で、カレント・ディレクトリに記録した変数を読み戻せます。
行列多項式とベクトルの積;;=:mt;(mt^2 + 2 mt + mt^-2) ~[1,2] =============================== [ 43. 83.75]
次のようなワンライナーを使って、シーケンス・データをグラフ表示できます。下で arsq(0,N,5/N) は 0, 0+5/N, 0+2*5/N, .... , 0+(N-1)*5/N, の値を返すジェネレータです。Python の range(..) は整数しか扱えず、また scipy.arange(..) は複素数列を扱えません。そのため arsq(..) を用意しました。
シーケンス・データのグラフ表示;;N=128;plotGr([sin( x^2 + 1) for x in arsq(0,N,5/N)])
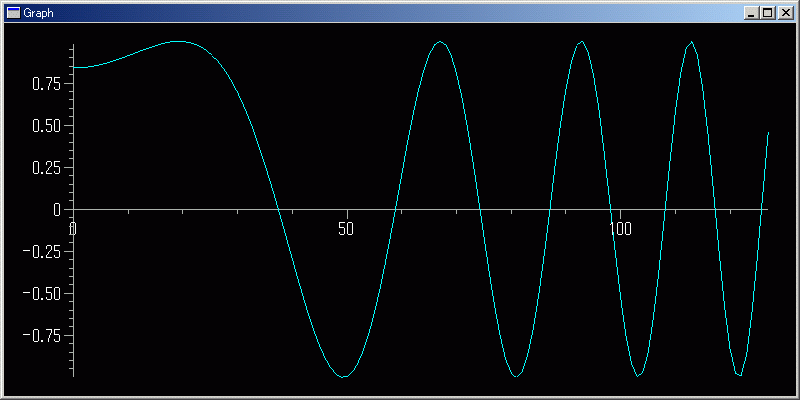
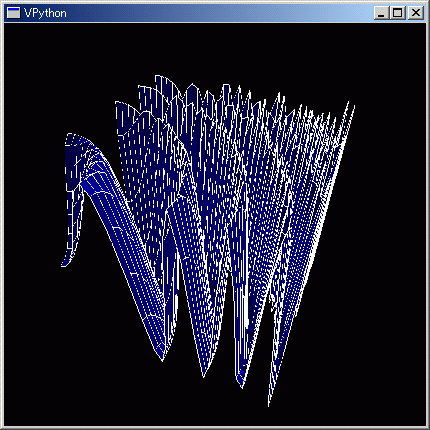
行列データの 3D グラフ表示;;N=32;renderMtrx(~[[sin( x^2 + y^2 ) for x in arsq(0,N,5/N)] for y in arsq(0,N,5/N)])
sympy python モジュールを利用することで、シンボリックな数式処理も可能になります。次のような具合です
代数式の展開;;((`x^3+2 `x+`y) (`x+3`y)).expand() =============================== 7*x*y + 2*x**2 + 3*y**2 + 3*y*x**3 + x**4 多項式のシンボル微分;;ts.diff(`x^3 + 2`x^2 + 3`x + 4,`x) =============================== 3 + 4*x + 3*x**2 関数のシンボル微分;;ts.diff(ts.sin(`x^2+`y^2),`x) =============================== 2*x*cos(x**2 + y**2) シンボル等式;;(`x (`y + `z)).expand() == `x `y + `x `z =============================== True sympy モジュール名はユーザー拡張ファイル sfCrrntIni.py に ts の名前で import して あります。また `x,`y,`z と`n_ も sympy シンボル変数として、sfCrrntIni.py にユーザ ー拡張変数として、定義してあるので、明示的な宣言なしに使えます。
次のように単位付きの物理定数を使った計算ができます
r=1cm`;(2^-24V`, eQ`/(4`π ε0` r) )
===============================
(5.96046447753906e-8/A*m**2*s**(-3)*kg, 1.43997584107973e-7/A*m**2*s**(-3)*kg)
備考 24ビット A/D コンバータの LSB:電圧精度は、一個の電子から 1cm 離れた位置の電位より小さい!
eQ` は電子の電荷であり、`πは円周率、ε0~ は真空の誘電率です
ユーザーによる変数名の拡張として、物理単位付きで定義してあります。
微細構造定数;;eQ`^2/(h`` c` 4 `π ε0`)
===============================
0.00729746120558574
備考:プランク定数:h`` 光速度:c`
単位付き計算でも、計算結果が無次元になれば、単位も付きません。分母だけなら下の物理量になります。
h`` c` 4 `π ε0`
===============================
3.51767575089232e-36*A**2*s**2
下のように、一行の式だけでマンデルブロー集合を計算できます。
;;N=128;def check(c,z=0,k=0):return k>500 and 500 or abs(z) < 2 and check(c,z**2+c,k+1) or k;mt=kzrs(N,N,int);for idx,(x,y) in enmasq( (-2,N,4/(N)),(2,N,-4/N)):mt[idx]=check(x+y `i);mt:=mt =============================== [[1 1 1 ..., 1 1 1] [1 1 1 ..., 1 1 1] [1 1 1 ..., 1 1 1] ..., [1 1 1 ..., 1 1 1] [1 1 1 ..., 1 1 1] [1 1 1 ..., 1 1 1]] =:mt;`print(mt[64,:]) =============================== [ 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 4 4 4 5 7 500 7 7 7 9 31 40 14 34 16 13 19 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 500 19 13 16 34 14 40 31 9 7 7 7 500 7 5 4 4 4 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
下の一行だけでマンデルブロー集合を計算すると同時に、表示させることさえ可能です。(Web ページ表示を最大にしてもらえば、この一行を画面内に収められる思います。)
;;N=128;def check(c,z=0,k=0):return k>500 and 500 or abs(z) < 2 and check(c,z^2+c,k+1) or k;dct={};for idx,(x,y) in enmasq((-2,N,4/N),(2,N,-4/N)):dct[idx]=check(x+y `i);plot3dRowCol(dct)
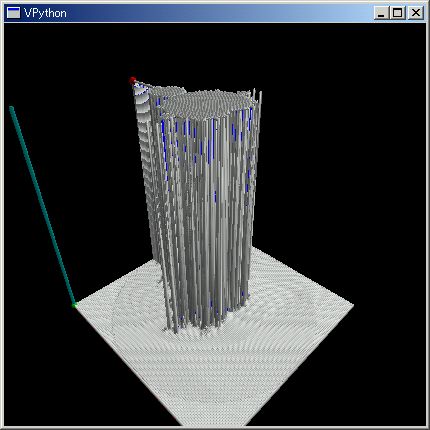
ワンライナーとはいえ、可読性も悪くないでしょう。check(..) 関数の中で場合分けを and/or を使っているのが技巧的かもしれませんが、許される範囲でしょう。下手な Java プログラムより短い文だけ処理内容を読み取りやすいと考えますが、如何でしょうか。
私も無理なワンライナーの使用は避けるべきだと考えます。可読性を下げてまでワンライナーにする意味はありません。でも数式・数値計算では if then else 構文がプログラムでのときほど必要ありません。ワン・ライナーで十分なことが多くあります。プリプロセッサを介在させることで、また行列に scipy.array を継承した krry テンソルを使うことで、多くの数学処理を、通常での数式記述に近い形のままにワンライナーで書けるようにできました。
数学ソフトを使うとき、大多数の計算は単純な確認計算のはずです。教科書や論文を読んでいく途中で、また研究ノートのメモ書きの途中で、自分の理解・推測を確認するために数学ソフトをちょっとだけ使うことが大部分のはずです。数学処理を行うプログラムを記述するのではなく、一行の数式で、具体例を計算させたり、グラフを表示させたりしたいことが多いはずです。プログラムを書き始めると、そちらにエネルギーが取られてしまい、読んでいる内容への集中、研究ノートへの集中が途切れてしまうからです。メモ書きの途中で計算させたいときは python sf によるワン・ライナーが役立つはずです。
でも複数行にわたるループ処理を書きたいなど、ワンライナーで書きにくいときは、躊躇なく複数行で書いてください。Python sf プリプロセッサは、一行文字列だけではなく、複数行で書かれる python sf のテキスト・ファイルも対象にできるのですから。(こちらについては別稿:sfShotAll.htm で説明します)
以下、python sf プリプロセッサで可能なワンライナーの主だった実例を見ていきます。とても全てを書ききれませんが、Mathematica, Matlab などを超えたと大言壮語するだけのものはあることを見てやってください。
コマンド実行本稿では、ワンライナーを「微細構造定数;;`eQ^2/(h`` c` 4 `π ε0`)」のように書いていきます。これは「;;」以降の文字列を取り出して引用符で囲み、「python testPy.py " Q^2/(h`` c` 4 `π ε0`)"」とコマンド・ラインで実行させることを意味しています。私自身は、そのような WZ エディタのマクロを組んで、ctrl + O + C 操作で、引用符の追加などの定型文字列処理をエディタ・マクロで実行させています。できましたら、お使いのエディタのコンソール・モードにそのようなマクロを組み込んで使ってみてください。
とり急ぎコードをテスト・実行させたいときには「;;」以降の文字列を " ... " と引用符で囲み、その前に「python testPy.py 」文字列を追加した文字列をエディタで作り、dos のコマンド・ラインに copy and paste し直して実行させてください。クリップ・ボードにあるコピーされた文字列は、dos 画面で「alt + space → E → p 」操作をするだけば dos 画面に貼り付けられます。
多くが、Python の文法と同じです。でも数式記述を容易にするため、プリプロセッサを働かせて、Python 文法を少し拡張しています。
ワンライナーで複数の式や文を書くときは ';' で区切ります。ワンライナー記述においては、関数や for ループはインデントができないので一つの文しか書けません。それでも以下のように、多くの計算がワンライナーで書けてしまいます。
和;;3+4
===============================
7
和 2;;a=3;b=4; a+b
===============================
7
差;;3-4
===============================
-1
差 2;;a=3;b=4; a-b
python -m testPy "a=3;b=4; a-b"
===============================
-1
べき乗 1;;a=3; a^128
===============================
11790184577738583171520872861412518665678211592275841109096961
備考:整数演算では、任意桁数の演算が可能です
^ 演算子をべき乗につかえるようにしています。
x^2 + 2 x + 1 などと書くとき楽であり、読みやすいからです。
べき乗 2;;a=3.0; a^128 # floating point number
===============================
1.17901845777e+061
べき乗 2;;a=3.0; a**128
===============================
1.17901845777e+061
備考:python のべき乗演算子 ** も使えます。
浮動小数点のべき乗 ;;(1/3)^3 # using from __future__ import division
===============================
0.037037037037
有理数のべき乗 2;;`Rat(1,3)^3
===============================
1/27
備考:`Rat(denominator, numerator) で sympy 有理数を返します。sfCrrntIni.py に定義してあります。
有理数のべき乗 1;;`Rat(2,3)^32
===============================
4294967296/1853020188851841
備考:`誤差無しでの有理数の計算が可能です
sf は ~[....] で行列やベクトルを表現できます。その行列やベクトルについても加減乗除算とべき乗算が可能です。でも sf は、この分野で有名な matlab 完全互換を目指していません。行列やベクトルは 0 インデックスから始めるべきだと主張します。Matlab とはのように 1 から始めるインデックスは使いません。sf の行列・ベクトルのほうが、数学で使うものに より近い、プログラム記述と相性が良いと主張します。
なお、python sf では、デフォルトではベクトルや行列は実数値、または複素数値とします。scipy パッケージでは array([1,2,3]) と書くと、整数値のベクトルになってしまいます。でも ~[1,2,3] は実数値のベクトルです。こうしないと、物理や工学分野での実数値しか使わない分野での記述が面倒になるからです。整数ベクトルだと、実数値を代入したとき、小数点以下が切り取られてしまうからです。
ベクトル宣言;;~[1,2,3]
===============================
[ 1. 2. 3.]
ベクトルのノルム;;norm(~[1,2,3])
===============================
3.74165738677
行列のノルム;;norm(~[[1,2,3],[4,5,6]])
===============================
9.53939201417
備考:norm(~[1,2,3,4,5,6]) と同じです
ベクトルとスカラーの積;;a=~[1,2,3];2 a
===============================
[ 2. 4. 6.]
ベクトルどうしの内積;;a=~[1,2,3];b=[4,5,6]; a b
===============================
32.0
行列宣言;;mt =~[ [1,2],[3,4]]
===============================
[[ 1. 2.]
[ 3. 4.]]
行列 * ベクトル;;mt =~[ [1,2],[3,4]];a=~[2,3]; mt a
===============================
[ 8. 18.]
scipy の array では行列とベクトルとの積には dot(mt,a) と書かねばならない
ベクトル * 行列 ;;mt =~[ [1,2],[3,4]];a=~[2,3]; a mt
===============================
[ 11. 16.]
ベクトル長が行列の column 長と同じならば、行列の左側からベクトルを掛けられる
縦ベクトル・横ベクトルの概念は python sf では使わない
逆行列 * ベクトルの1;;mt =~[ [1,2],[3,4]];a=~[2,3]; mt^-1 a
===============================
[-1. 1.5]
逆行列 * ベクトルの2;;mt =~[ [1,2],[3,4]];a=~[2,3]; 1/mt a
===============================
[-1. 1.5]
<a|行列|b> ;;mt =~[ [1,2],[3,4]];a=~[2,3]; b=~[4,5]; a mt b
===============================
124.0
<複素ベクトル a|行列|b> ;;mt =~[ [1+`i,2],[3,4]];a=~[2,3]; b=~[4,5]; a.c mt b
===============================
(124+8j)
a.c によってベクトル a の共役ベクトルを返させる
python sf では左側のベクトルについて、「.c」で明示的に共役ベクトルとする
自動的に共役ベクトルにすると、Minkowsky 空間での行列・ベクトル計算がやりにくくなる
Python sf ではテンソルも扱えます。一般相対論での計算を主な用途として考えています。三階以上のテンソルでは逆行列を定義できませんが、「環」としての加減乗算が可能です。また「^」演算子を行列やベクトルと組み合わせたときは、テンソルでの外積演算の意味にしています。
ベクトルのダイアディック・外積演算 1;;~[1,2,3]^~[4,5,6]
===============================
[[ 4. 5. 6.]
[ 8. 10. 12.]
[ 12. 15. 18.]]
三つのベクトルの外積演算;;~[1,2,3]^~[4,5,6]^[8,9]
===============================
[[[ 32. 36.]
[ 40. 45.]
[ 48. 54.]]
[[ 64. 72.]
[ 80. 90.]
[ 96. 108.]]
[[ 96. 108.]
[ 120. 135.]
[ 144. 162.]]]
「三つのベクトルの外積」 * ベクトル;;~[1,2,3]^~[4,5,6]^[8,9] [1,2]
===============================
[[ 104. 130. 156.]
[ 208. 260. 312.]
[ 312. 390. 468.]]
テンソルの縮約:
「三つのベクトルの外積」結果にたいし、 0,1 インデックスでの縮約を行い 2 インデックスを残します
(~[1,2,3]^~[4,5,6]^[8,9])[{0,1}]
===============================
[ 256. 288.]
Levi Civita tensor;;`εL
===============================
[[[ 0. 0. 0.]
[ 0. 0. 1.]
[ 0. -1. 0.]]
[[ 0. 0. -1.]
[ 0. 0. 0.]
[ 1. 0. 0.]]
[[ 0. 1. 0.]
[-1. 0. 0.]
[ 0. 0. 0.]]]
備考:Levi Civita テンソル `εL をユーザー拡張 sfCrrntIni.py に定義しています
Levi Civita tensor によるベクトルの外積 a x b;;a=~[1,2,3];b=~[4,5,6];a `εL b
===============================
[-3. 6. -3.]
Wedge 積;;`Λ([1,2,3],[4,5,6])
===============================
[[ 0. -3. -6.]
[ 3. 0. -3.]
[ 6. 3. 0.]]
Wedge 積;;`Λ([1,2,3,4],[4,5,6,7], [7,8,9,11])
===============================
[[[ 0. 0. 0. 0.]
[ 0. 0. 0. -3.]
[ 0. 0. 0. -6.]
[ 0. 3. 6. 0.]]
[[ 0. 0. 0. 3.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. -3.]
[-3. 0. 3. 0.]]
[[ 0. 0. 0. 6.]
[ 0. 0. 0. 3.]
[ 0. 0. 0. 0.]
[-6. -3. 0. 0.]]
[[ 0. -3. -6. 0.]
[ 3. 0. -3. 0.]
[ 6. 3. 0. 0.]
[ 0. 0. 0. 0.]]]
備考:sfCrrntIni.py に、 任意ベクトル次元の wedge 積関数 `Λ を定義してあります。
Python sf はプリプロセッサであり、python で扱える文字列に変換させてから、python パッケージ郡に実際の計算を行わせています。このプリプロセッサにより、数式に特化した簡便な記述を可能にしてしています。
変数の前後に逆シングル・クォートを付加した変数をユーザー変数として python 変数と区別しています。sfCrrntIni.py ファイル内にユーザー変数を定義・宣言してやることで、python sf で使えるようになります。配布例では、kg` などの単位系、ε0`:真空の誘電率などの物理定数、`x などの sympy シンボル変数などをユーザー変数として宣言・定義してあります。ユーザーが自分で自由に宣言・定義できます。以下のような具合に使っています。
単位付きの光速度;;c` =============================== 299792458.0/s*m 純虚数;;`i =============================== 1j 数学表記に近い python sf 式;;exp( 2/3 pi `i) =============================== (-0.5+0.866025403784j)
変数名にギリシャ文字と計算記号:∇□∂△を使えるようにしています。python2.4/2.5 でも、これらの記号を使えます。ギリシャ文字や微分記号を使えると便利ですよ。
Python sf プリプロセッサで使える変数名は、正規表現で書くと下のように定義されています。これで、どんな変数名を使えるか判断できると思います。
ur"[_A-Za-zα-ωΑ-Ω∇□∂△`][\wα-ωΑ-Ω∇□∂△]*[_`]*"
sfCrrntIni.py ファイルでは、Pauli 行列「`σx,`σy,`σz」を宣言・定義してあります。
`σx =============================== [[ 0. 1.] [ 1. 0.]] ---- ClTensor ---- `σy =============================== [[ 0.+0.j 0.-1.j] [ 0.+1.j 0.+0.j]] ---- ClTensor ---- `σx `σy + 3`σz =============================== [[ 3.+1.j 0.+0.j] [ 0.+0.j -3.-1.j]] ---- ClTensor ----
`σx ~^ `σy =============================== [[ 0.+2.j 0.+0.j] [ 0.+0.j 0.-2.j]] ---- ClTensor ----
特に python の range(..) 関数は整数値ループ・パラメータを与えるのに頻繁に使われます。でも実数値/複素数値の数列を扱かったり、二次元/三次元でのループを多用する科学技術計算では、range(..) だけでは、面倒なときが多くあります。Python sf では、科学計算のループ処理で便利な arsq, masq, mrng, enmasq といった数列生成関数をを幾つか用意してあります。
range:start, stop, step 引数:1;; range(2,15,3) =============================== [2, 5, 8, 11, 14] start:default 0, stop, step:default 1です;; range(15) =============================== [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14] range を使ったループ記述;;for i in range(2,15,3):print i^2 4 25 64 121 196 ------------------------------- None
でも、range(.) 引数は整数しか許されません。実数を使うためには、scipy の arange(..) 関数を使います。
range:start, stop, step 引数:1;; arange(2.1,15,3.2) =============================== [ 2.1 5.3 8.5 11.7 14.9] start:default 0, stop, step:default 1です;; arange(1.1,15) =============================== [ 1.1 2.1 3.1 4.1 5.1 6.1 7.1 8.1 9.1 10.1 11.1 12.1 13.1 14.1] range を使ったループ記述;;for db in arange(2.1,15,3.2):print db^2 [ 1.1 2.1 3.1 4.1 5.1 6.1 7.1 8.1 9.1 10.1 11.1 12.1 arange(..) が返すのはベクタであり、ベクタ演算が可能です;;2 arange(2.1,15,3.2) =============================== [ 4.2 10.6 17. 23.4 29.8] enumerate(arange(..)) で整数インデックスと数列の組を返します for idx, val in enumerate(arange(2.1,15,3.2)):print 'idx:', idx, ' val',val idx: 0 val 2.1 idx: 1 val 5.3 idx: 2 val 8.5 idx: 3 val 11.7 idx: 4 val 14.9 ------------------------------- None
arange(..) は、start, stop, step 引数を与えるため、start と stop の間に大小関係が定義できる引数までしか指定できません。複素数やベクトルの数列を作れません。そのために arsq(..) を sf.py に用意してあります。start, size, step 引数を与えます。size はシーケンスの長さであり整数ですが、start, step はベクトル演算が可能であれば、複素数、ベクトル等なんでもかまいません。
複素数数列;;arsq(1+`i,5,3`i) =============================== ((1+1j), (1+4j), (1+7j), (1+10j), (1+13j)) ベクトルの数列;;arsq(~[3,4],5,~[1,2]) =============================== (krry([ 3, 4], dtype = scipy.float64), krry([ 4, 6], dtype = scipy.float64), krry([ 5, 8], dtype = scipy.float64), krry([ 6, 10], dtype = scipy.float64), krry([ 7, 12], dtype = scipy.float64)) ベクトル数列の pretty print;;import pprint as pp;pp.pprint(arsq(~[3,4],5,~[1,2])) (krry([ 3, 4], dtype = scipy.float64), krry([ 4, 6], dtype = scipy.float64), krry([ 5, 8], dtype = scipy.float64), krry([ 6, 10], dtype = scipy.float64), krry([ 7, 12], dtype = scipy.float64)) =============================== None
科学計算では、二次元/三次元でのデータを扱うことが多いのですが、range(.), arange(.), arsq(.) では、二重ループ/三重ループで記述せねばなりません。それが面倒なので mrng(.), masq(.) を sf.py に用意してあります。多重ループでもインデックスを使えるように enmasq を用意してあります。
for tplIdx in mrng(3,4):print tplIdx (0, 0) (0, 1) (0, 2) (0, 3) (1, 0) (1, 1) (1, 2) (1, 3) (2, 0) (2, 1) (2, 2) (2, 3) ------------------------------- None for tplIdx in masq((1,3,0.1),(2,4,1.2)):print tplIdx (1.0, 2.0) (1.0, 3.2000000000000002) (1.0, 4.4000000000000004) (1.0, 5.5999999999999996) (1.1000000000000001, 2.0) (1.1000000000000001, 3.2000000000000002) (1.1000000000000001, 4.4000000000000004) (1.1000000000000001, 5.5999999999999996) (1.2, 2.0) (1.2, 3.2000000000000002) (1.2, 4.4000000000000004) (1.2, 5.5999999999999996) ------------------------------- None for idx, tplData in enmasq((1,3,0.1),(2,4,1.2)):print 'idx:',idx, ' tplData:',tplData idx: (0, 0) tplData: (1.0, 2.0) idx: (0, 1) tplData: (1.0, 3.2000000000000002) idx: (0, 2) tplData: (1.0, 4.4000000000000004) idx: (0, 3) tplData: (1.0, 5.5999999999999996) idx: (1, 0) tplData: (1.1000000000000001, 2.0) idx: (1, 1) tplData: (1.1000000000000001, 3.2000000000000002) idx: (1, 2) tplData: (1.1000000000000001, 4.4000000000000004) idx: (1, 3) tplData: (1.1000000000000001, 5.5999999999999996) idx: (2, 0) tplData: (1.2, 2.0) idx: (2, 1) tplData: (1.2, 3.2000000000000002) idx: (2, 2) tplData: (1.2, 4.4000000000000004) idx: (2, 3) tplData: (1.2, 5.5999999999999996) ------------------------------- None
enmasq(.) を使うと、複素平面状での複素数値分布を複素数値行列で表現できます。この形式での複素数値行列を複素関数 3D 表示で多用します
enmasq による行列的な辞書;;dct={};for idx, (x,y) in enmasq((1,3,0.1),(2,4,1.2)):dct[idx]= x+y `i;dct
===============================
{(0, 1): (1+3.2000000000000002j), (1, 2): (1.1000000000000001+4.4000000000000004j), (0, 0): (1+2j), (2, 1): (1.2+3.2000000000000002j), (0, 2): (1+4.4000000000000004j), (2, 0): (1.2+2j), (1, 3): (1.1000000000000001+5.5999999999999996j), (2, 3): (1.2+5.5999999999999996j), (2, 2): (1.2+4.4000000000000004j), (1, 0): (1.1000000000000001+2j), (0, 3): (1+5.5999999999999996j), (1, 1): (1.1000000000000001+3.2000000000000002j)}
enmasq による行列;;dct={};for idx, (x,y) in enmasq((1,3,0.1),(2,4,1.2)):dct[idx]= x+y `i;krry(dct)
===============================
[[ 1. +2.j 1. +3.2j 1. +4.4j 1. +5.6j]
[ 1.1+2.j 1.1+3.2j 1.1+4.4j 1.1+5.6j]
[ 1.2+2.j 1.2+3.2j 1.2+4.4j 1.2+5.6j]]
使用頻度の高い 2D グラフ表示のための plotGr(..) 関数と、タイムチャーチ表示のための plotTmCh(..) を用意しています。plotGr(..) は vpython の gcurve を使った 30 行弱の関数で実装しました。plotTmCh(..) は pylab パッケージの plot 関数を使って 40 行弱で実装しました。plotGr/plotTmCh 関数の機能で不満なときは、ユーザー側で必要なグラフ表示関数を容易に実装できます。
plotGr(..) 関数の引数には任意の実数値シーケンスデータを渡せます。横軸/縦軸のレンジは plotGr(..) 関数側で、引数データを元に定めます。最小の手間でグラフ表示することを目的に plotGr(..) 関数を作ってあります。
plotGr([1,3,2,4,0])
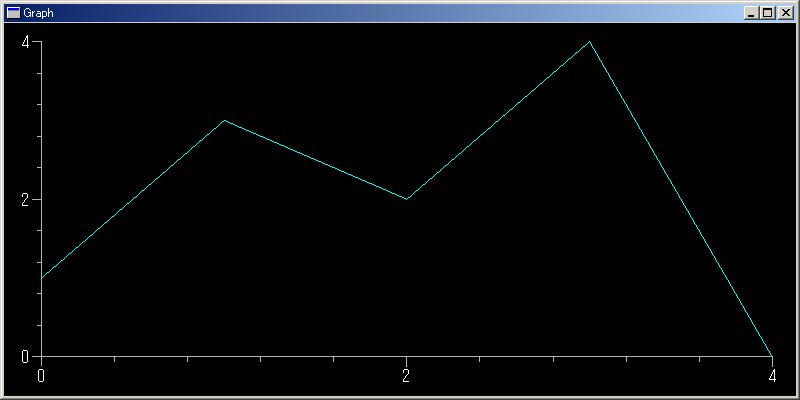
複数関数の重ね書き、グラフの色指定も可能です。
plotGr([1,3,2,4,0]);plotGr([1, 4, 2.5, 4.5, 0.5, 1],color=green);
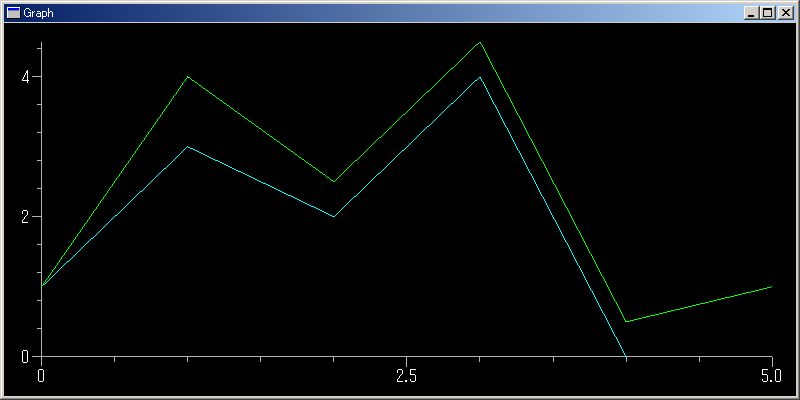
Python のリスト内包表記を使えば、任意の関数の/任意の定義域の グラフ表示が可能です。
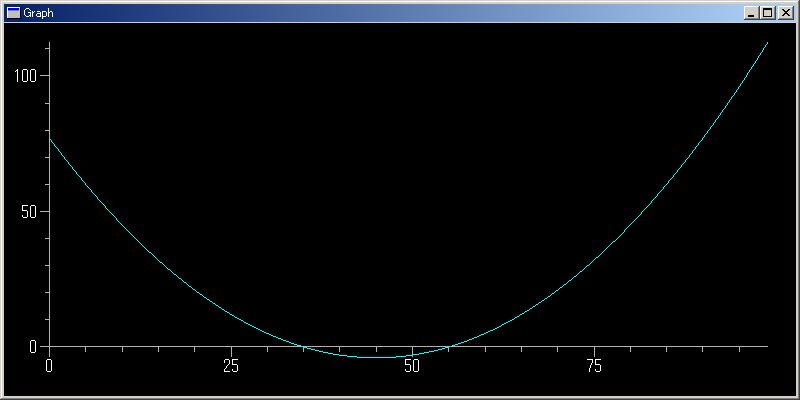
N=100; plotGr([x**2 +2*x-3 for x in arsq(-10,N,20/N)])
N=100;plotGr([ss.gamma(x) for x in arsq(0.1,N,5/N)])
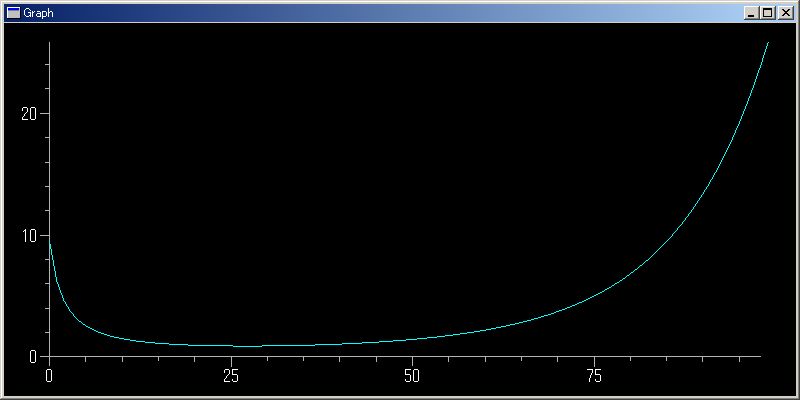
python sf は、このグラフ表示機能が一番使われると推測しています。
デジタル回路で必要となるタイム・チャート表示のために plotTmCh(..) 関数を設けました。)plotTmCh (..) の引数は行列データです。行列の横成分が、一つのタイム・チャートデータになります。
N=10; mt=kzrs(2,2N);mt[0,:] = (0,1)*N;mt[1,0:N]=range(N);mt[1,N:2N]=range(N);plotTmCh(mt)
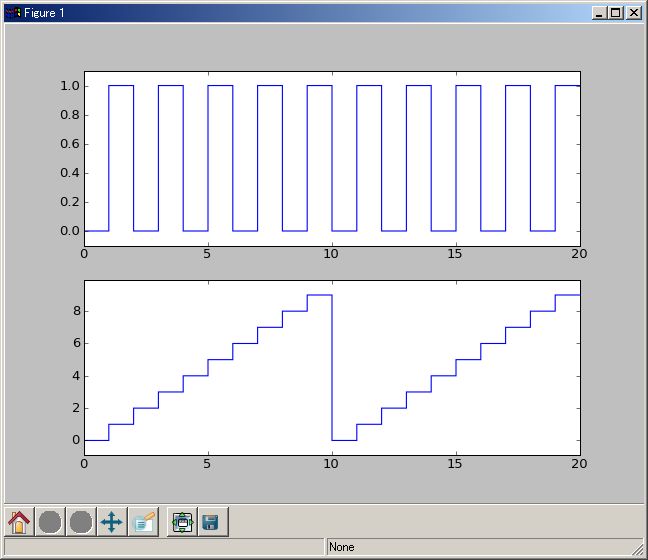
私は plotTmCh(..) 関数をヒストグラム表示にも流用しています。
plotTmCh([1, 4, 2.5, 4.5, 0.5, 1])
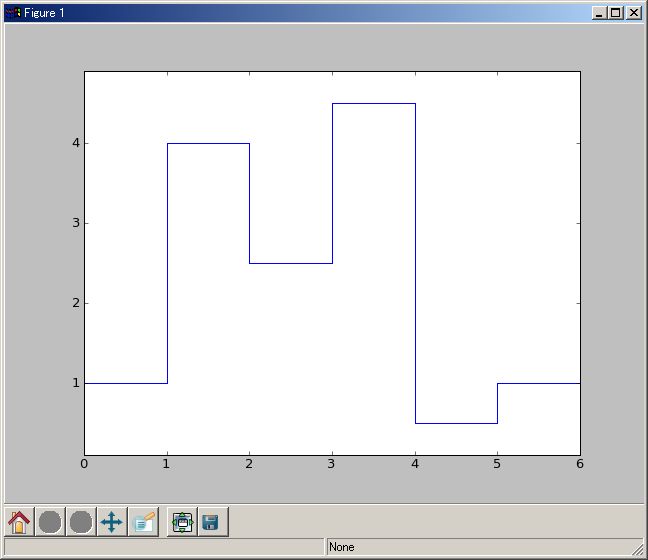
plotTmCh(..) 関数の実装は、ユーザーが自分にとって必要な関数を作成するときの具体例にもなっていると思います。
複素数値関数を二次元、三次元の図で表示するために、 「kk-RGB 表示」と名付けた複素数値分布を提案します。複素平面の位置を下の図のような色の分布で表現することを提案します。

例えば多項式 z^3+z^2-2 の定義域を複素数値に広げたとの値の変化は、下のように kkRGB 表示されます
//@@
def f(z):
return z^3+z^2-2
S=-3;N=400
import Image as Im
imAt = Im.new('RGB', (N,N))
clAt = ClCplxColor()
for index, (x,y) in zip(mrng(N,N), sf.masq([-S+S/N, N, 2*S/N],[S-S/N, N, -2*S/N]) ):
imAt.putpixel( index, clAt.GetIntColor(f(x+`i y)) )
imAt.save('test.jpg')
//@@@
//copy \#####.### temp.py /y
//testPy.py -fs temp.py
//__tempConverted.py
start test.jpg
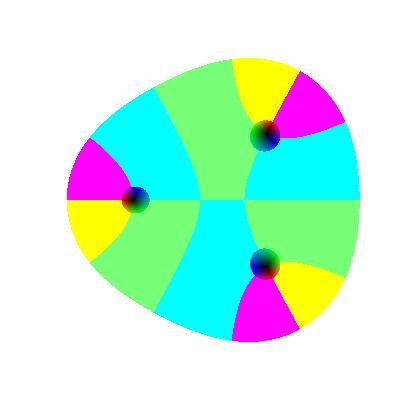
三つの黒い丸の中が、多項式の極の周りの、絶対値が 1 より小さい領域です。RGB 三色がアナログ的に変化しています。外側の白い領域が、この多項式の絶対値が 10 より大きい領域です。紫、黄色、緑、青の四色でデジタル的に表示されているのが、多項式の絶対値が 1 より大きくて 10 より小さい領域です。この多項式の絶対値の分布、位相回転の様子をイメージできますでしょうか。
2D kk-RGB 表示を使う頻度は少ないので、python sf は、ワンライナーで 2D kkRGB表示するようには作ってありません。Python sf プロプロセッサで __tempConverted.py ファイルを生成させて実行しています。「■ kkRGB 3D グラフ表示 」で説明するように、ワンライナーによる 3D kkRGB 表示を可能にしてあります。kk-RGB 表示という、複素数値の位相を RGB の三色の変化によって表示する方法を理解してもらうために、「■ kk-RGB 2D 表示」の節を挿入しました。
python sf では 3D グラフ表示もワンライナーで扱えるのが自慢です。ここでは renderMtrx(..)/renderMtCplxWithRGB(..) の二つを説明します。
実数値関数の 3D 表示は renderMtrx(..) が便利です。引数には実数値行列を渡します。
N=64;mt={};for idx, (x,y) in enmasq([3,N,-6/N],[-3,N,6/N]):mt[idx]=sin( x^2 + y^2 )/sqrt(x^2+y^2);renderMtrx(mt)
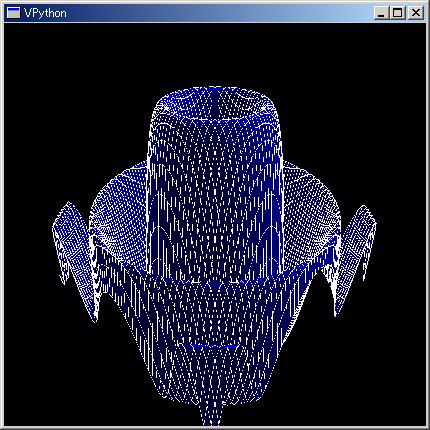
コンソールには行列の最小値/最大値を表示します。
index:(21, 29) max: 0.851057 : 0.851056954696 index:(11, 23) min:-0.463254 : -0.46325380339
引数の行列値は、辞書:dict/二重になった list /scypy.array/sf.ClTensor が使えます。
renderMtCplxWithRGB(..) の引数に複素数値行列を渡してやれば、高さを複素数値の絶対値/位相回転を kk-RGB で表した 3D 表示を行います。下のような具合です。
dct={};N=32;for idx, (x,y) in enmasq((-3,N,6/N), (1,N,-2/N)):dct[idx]=sin(x + `i y);renderMtCplxWithRGB(dct)
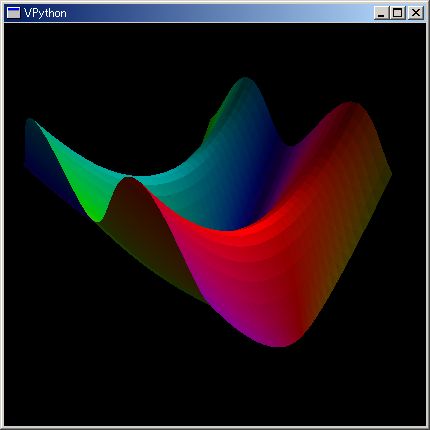
この kkRGB 3D 表示は、vpython の面表示機能を使って 300 行弱で実装してあります。必要ならば、ユーザー固有の 3D 表示関数を自分で記述できます。
dct={};N=32;for idx, (x,y) in enmasq((-3,N,6/N), (3,N,-6/N)):dct[idx]=tan(x + `i y);renderMtCplxWithRGB(dct)
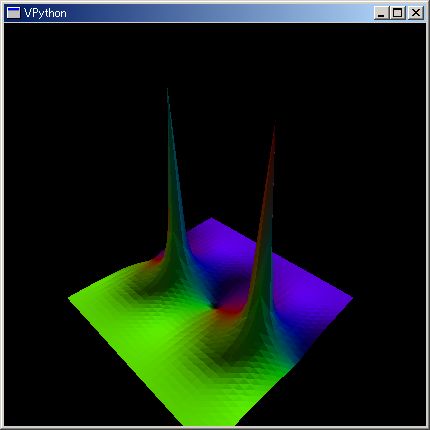
上は tan 解析関数を kkRGB 3D 表示させました。tan 関数の複素領域における位相回転が良く判ると思います。
また二次元行列データを作るのに enmasq(..) ジェネレータを使っています。二重ループを作らずに済ませています。enmasq(..) の威力を判ってもらえますでしょうか。
dct={};N=32;for idx, (x,y) in enmasq((-2,N,4/N), (2,N,-4/N)):dct[idx]=arctan(x + `i y);renderMtCplxWithRGB(dct)
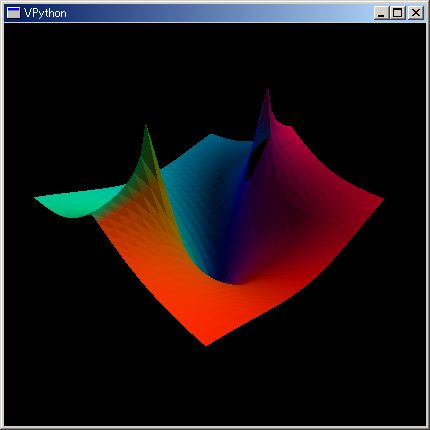
上は、arctan(.) 解析関数の kkRGB 3D 表示です。
マウスで回転させ、さらに少し拡大してみました
両サイドの尖った稜線で、リーマン面が交わっています。arctan(..) 関数の複素平面領域での形・位相回転の様子をイメージできますでしょうか。
解析関数ですから極以外では滑らかに繋がっていなければならないのですが、リーマン面が交わる個所では鋭角になってしまいます。arctan(..) が多価関数になっていないためです。
sympy モジュールを利用することで、数式文字列の抽象的段階のままでの演算処理も可能になります。単なる数値計算以上のことができます。
f=`x+`y; g= `x-`y;f g =============================== (x - y)*(x + y) f=`x+`y; g= `x-`y;ts.simplify(f g) =============================== x**2 - y**2
sympy モジュールは短縮名 ts で sfCrrntIni.py で宣言してあります。sympy モジュールに用意されている変数や関数は ts.?????? の形式で(e.g. ts.simplifi) 使います。
`x,`y,`z, `t, `p,`q, `n_ は sympy.Symbol シンボル変数として sfCrrntIni.py に宣言済みなので、python sf 式では宣言無しに使えます。
`x,`y,`z に関数一次微分について ∂x,∂y,∂z,∂t,∂p,∂q, `dx,`dy,`dz,`dt, `dp,`dq が sfCrrntIni.py に宣言してあります。次のように使えます
∂x(ts.sin(`x^2+`y^2)) =============================== 2*x*cos(x**2 + y**2) `dy(ts.sin(`x^2+`y^2)) =============================== 2*y*cos(x**2 + y**2) f=1/ts.sqrt(`x^2+`y^2+`z^2); ∂z(f) =============================== -z/(x**2 + y**2 + z**2)**(3/2) f=1/ts.sqrt(`x^2+`y^2+`z^2 - `t); `dt(f) =============================== 1/(2*(-t + x**2 + y**2 + z**2)**(3/2)) H=`p^2 + `q^2;q`=-∂p(H) Waring: don't use assignment at last sentence.We ignore the assignment. =============================== -2*p
sympy での計算結果は sympy でのシンボリックな数式を返しています。それらの数式が返す実際の数値を計算させるには Float(..)/Cmplx(..) 関数を使います。Float/Cmplx(..) 関数も sfCrrntIni.py に定義してあります。
H=`p^2 + `q^2;q`=-∂p(H);Float(q`, 1, ) =============================== -1.0 H=`p^2 + `q^2;q`=-∂p(H);Float(q`, 1,2.5) -2*p dosen't have two symbols:(x,y), (x,t) ,(p,q), (p,t), (q,t) variables. at excecuting:Float(k_q_bq____, 1,2.5)
q` は一変数 p のみの式なので、その数値を求めるために二つ p,qパラメータ値を与えるとエラーになります。
∇, `grad、 `div, △,`Lablacian も sfCrrntIni.py に用意してあります。
V=1/ts.sqrt(`x^2+`y^2+`z^2); ∇(V) =============================== (-x/(x**2 + y**2 + z**2)**(3/2), -y/(x**2 + y**2 + z**2)**(3/2), -z/(x**2 + y**2 + z**2)**(3/2)) V=1/ts.sqrt(`x^2+`y^2); `grad(V) =============================== (-x/(x**2 + y**2)**(3/2), -y/(x**2 + y**2)**(3/2)) V=1/ts.sqrt(`x^2+`y^2); `div(`grad(V)) =============================== 3*x**2/(x**2 + y**2)**(5/2) + 3*y**2/(x**2 + y**2)**(5/2) - 2/(x**2 + y**2)**(3/2) V=ts.log(1/ts.sqrt(`x^2+`y^2)); △(V) =============================== -2/(x**2 + y**2) + 2*x**2/(x**2 + y**2)**2 + 2*y**2/(x**2 + y**2)**2 V=1/ts.sqrt(`x^2+`y^2); △(V) =============================== 3*x**2/(x**2 + y**2)**(5/2) + 3*y**2/(x**2 + y**2)**(5/2) - 2/(x**2 + y**2)**(3/2) V=1/ts.sqrt(`x^2+`y^2+`z^2); `Laplacian(V) =============================== 3*x**2/(x**2 + y**2 + z**2)**(5/2) + 3*y**2/(x**2 + y**2 + z**2)**(5/2) + 3*z**2/(x**2 + y**2 + z**2)**(5/2) - 3/(x**2 + y**2 + z**2)**(3/2)
log(1/r(x,y)) や 1/r(x,y,z) のラプラシアンが 0 の数式になっていません。これが現在の sympy の能力です。でも下のように常に 0 を返す関数になっており、正しい計算結果です。
x,y=1,2;-2/(x**2 + y**2) + 2*x**2/(x**2 + y**2)**2 + 2*y**2/(x**2 + y**2)**2 =============================== 0.0 x,y,z=1,2,3;3*x**2/(x**2 + y**2 + z**2)**(5/2) + 3*y**2/(x**2 + y**2 + z**2)**(5/2) + 3*z**2/(x**2 + y**2 + z**2)**(5/2) - 3/(x**2 + y**2 + z**2)**(3/2) =============================== 6.93889390391e-018
z_ について説明する
添付してある tnRcGn.py モジュールには無限再帰を可能にする generator 関数クラスと itertools を拡張してインデックス[...] を使えるようにした python コードが書いてあります。ユーザーが自作モジュールを python sf から呼び出して使うときの具体例にもなっています。
python の itertools ビルトイン・モジュールはシーケンス・データを弄繰り回すのに便利です。でも、数列を扱うのには、少しばかり不便です。serieseVar[3:9] などと [..] __getitem__(..)を扱えないからです。でも 標準の python で扱えなくても、ユーザー側で扱えるように細工できてしまうのが、python の良い所です。__getitem__ を追加した itertools の修正版を、tnRcGn.py に入れてあります。以下のように無限数列を自在に扱えます。sfCrrntIni.py の中で tnRcGn.py モジュールには tn の別名を割り当ててあります。
自然数列;;tn.count()[:10] =============================== [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] 3 から始まる自然数列;;tn.count(3)[:10] =============================== [3, 4, 5, 6, 7, 8, 9, 10, 11, 12] 繰り返しシーケンス;;tn.cycle([2,9,5,7])[:10] =============================== [2, 9, 5, 7, 2, 9, 5, 7, 2, 9] 一つの値の繰り返;;tn.repeat(2)[:10] =============================== [2, 2, 2, 2, 2, 2, 2, 2, 2, 2] 数列要素への関数の適用;;tn.imap(λ x:x^2, tn.count())[:10] 二つの数列の交互配置;;tn.izip(tn.count(),tn.cycle([2,9,5,7]))[:10] =============================== [(0, 2), (1, 9), (2, 5), (3, 7), (4, 2), (5, 9), (6, 5), (7, 7), (8, 2), (9, 9)] 数列を繋げる;;tn.chain([1]*4,tn.count(3))[:10] =============================== [1, 1, 1, 1, 3, 4, 5, 6, 7, 8]
これらを組み合わせれば、望みの数列を簡単に記述できるでしょう。例えば√(2) の連分数表記を次のように python sf 式で記述できます。
√2 の正則連分数列 10 までの値;;N=10;sqAt = tn.chain([1],tn.repeat(2))[:N]; reduce(λ x,y: 1/x +y, sqAt[::-1], `Rat(2)) =============================== 8119/5741
「tn.chain([1],tn.repeat(2))」で√2 の下の連分数数列を記述できます。その具体的な数値は「reduce(λ x,y: 1/x +y, sqAt[::-1], `Rat(2))」で計算させられます。「sqAt[::-1]」 によりお尻の側から計算させます。初期値を `Rat(2) と sympy 有理数とすることで、誤差無しの有理数計算をさせています。
1
√2 = 1 + --------------------------
1
2 + ----------------------
1
2 + ------------------
1
2 + --------------
1
2 + ----------
..........
;;lst=[0,1];def fib(n):return -1 if n<0 else list[n] if n <;len(lst) else fib(n-1)+fib(n-2);[fib(x) for x in range(10)] ;;lst=[0,1];def fib(n):return( n<0 and -1) or (n < len(lst) and lst[n]) or fib(n-1)+fib(n-2);[fib(x) for x in range(10)] =============================== [-2, 1, -1, 0, -1, -1, -2, -3, -5, -8] ;;lst=[0,1];def fib(n): -1 if n<0 else lst[n] if (n < len(lst) else lst.append(fib(n-1)+fib(n-1)) or fib(n);tn.idx(fib)[:10] ;;\lng\python25\python -m testPy "lst=[0,1];def fib(n): -1 if n<0 else lst[n] if (n < len(lst) else lst.append(fib(n-1)+fib(n-1)) or fib(n);fib)[10]" ;;lst=[0,1];def fib(n): -1 if n<0 else lst[n] if (n < len(lst) else lst.append(fib(n-1)+fib(n-1)) or fib(n);fib)[10] ;;lst=[0,1];def fib(n):yield( n<0 and -1) or (n < len(lst) and lst[n]) or fib(n-1)+fib(n-1);tn.idx(fib)[:10]
;;N=4;tn.imap(λ n:4/ts.pi ts.sin( (2 n + 1) `x)/(2 n + 1), tn.count())[:N] =============================== [4/pi*sin(x), (4/3)/pi*sin(3*x), (4/5)/pi*sin(5*x), (4/7)/pi*sin(7*x)]
Python sf のワン・ライナー文でも、十分に矩形波のフーリエ級数式を表現できていると思います。如何でしょうか。
これをグラフにして、フーリエ級数の長さによる近似の違いを表示します。
L=20;K=128;for N in range(3,L,5):plotGr([ sum(tn.imap(λ n:4/ts.pi ts.sin( (2 n + 1) `x)/(2 n + 1), tn.count())[:N]).subs(`x,x).evalf() for x in arsq(-pi,K,2 pi/K)], color=blue + ~[N/L,N/L,0])
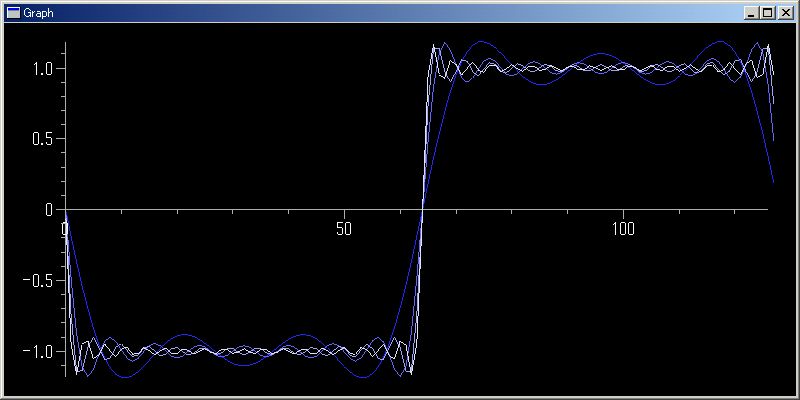
実際に試行錯誤している過程では、下の二つの python sf スクリプトを、 N を変えて何回か実行することになると思います。上の例のように、少し無理のあるワンライナーを書く必要はありません。
;;N:=10;test:=tn.imap(λ n:4/ts.pi ts.sin( (2 n + 1) `x)/(2 n + 1), tn.count())[:N] =============================== [4*sin(x)/pi, 4*sin(3*x)/(3*pi), 4*sin(5*x)/(5*pi), 4*sin(7*x)/(7*pi), 4*sin(9*x)/(9*pi), 4*sin(11*x)/(11*pi), 4*sin(13*x)/(13*pi), 4*sin(15*x)/(15*pi), 4*sin(17*x)/(17*pi), 4*sin(19*x)/(19*pi)] =:test,N;K=128;plotGr([sum([Float(f,x) for f in test]) for x in arsq(0,K,pi/K)]) ×=:test;N=10;K=128;plotGr([sum(test).subs(`x,x).evalf() for x in arsq(0,K,pi/K)])
24 ヶ月返済、年利 23% 借入金 100 万円での元利金等払い返済における元本返済分と利息返済分の計算です。少し長い式ですが、全画面ならば一行で収まると思います。
N=24;T=1e6;r=0.23/12;RM=1+r;ll=[~[T,0,0]];def f(i):return ll[i-1][0]*(1-RM)/(1-RM^(N+1-i));for i in range(1,N+1):ll.append(~[ll[i-1][0]-f(i), f(i),ll[i-1][0] r]) ;mt:=krry(ll)
===============================
[[ 1.00000000e+06 0.00000000e+00 0.00000000e+00]
[ 9.66793361e+05 3.32066394e+04 1.91666667e+04]
[ 9.32950261e+05 3.38431000e+04 1.85302061e+04]
[ 8.98458501e+05 3.44917594e+04 1.78815467e+04]
[ 8.63305650e+05 3.51528514e+04 1.72204546e+04]
[ 8.27479035e+05 3.58266144e+04 1.65466916e+04]
[ 7.90965744e+05 3.65132912e+04 1.58600148e+04]
[ 7.53752615e+05 3.72131293e+04 1.51601768e+04]
[ 7.15826234e+05 3.79263809e+04 1.44469251e+04]
[ 6.77172931e+05 3.86533032e+04 1.37200028e+04]
[ 6.37778773e+05 3.93941582e+04 1.29791478e+04]
[ 5.97629560e+05 4.01492129e+04 1.22240931e+04]
[ 5.56710820e+05 4.09187395e+04 1.14545666e+04]
[ 5.15007805e+05 4.17030153e+04 1.06702907e+04]
[ 4.72505482e+05 4.25023231e+04 9.87098293e+03]
[ 4.29188531e+05 4.33169510e+04 9.05635507e+03]
[ 3.85041339e+05 4.41471925e+04 8.22611351e+03]
[ 3.40047991e+05 4.49933470e+04 7.37995899e+03]
[ 2.94192272e+05 4.58557195e+04 6.51758650e+03]
[ 2.47457651e+05 4.67346208e+04 5.63868521e+03]
[ 1.99827283e+05 4.76303677e+04 4.74293831e+03]
[ 1.51284000e+05 4.85432831e+04 3.83002293e+03]
[ 1.01810304e+05 4.94736960e+04 2.89961001e+03]
[ 5.13883624e+04 5.04219419e+04 1.95136417e+03]
[ 0.00000000e+00 5.13883624e+04 9.84943613e+02]]
残っている元本 返済金の元本分 返済金の利息分
この式の肝は等比級数の和の公式の逆数 (1-RM)/(1-RM^(N+1-i) です。
P0*(1-RM^n)/(1-RM) # T == P0 + P0*RM + P0*RM^2 + ... + P0*RM^(n-1) ---- (4)式
各月の「返済金の元本分 + 返済金の利息分」を足してみると、一定の「52373円」になっています。元本の減少分と、残り支払い回数の減少分が打ち消しあって一定になります。このため「元利金等」と言われています。
=:mt; N=len(mt);~[mt[i,1]+mt[i,2] for i in range(N)] =============================== [ 0. 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986 52373.30602986]
この返済金の元本分だけを足し合わせてみると、最初に借りた 100 万円になっています。
=:mt; N=len(mt);sum([mt[i,1] for i in range(N)]) =============================== 1000000.0
残っている元本も計算できているので、借り換えシミュレーションも簡単にできます。御自分でも色々と計算してみてください。
N 次元ラプラシアン偏微分方程式を数値的に解く solveLaplacian(.) 関数を用意してあります。
∂^2 ∂^2 (------- + ------- + ...) ψ == 0 ∂x^2 ∂y^2
境界条件をデフォルトの周囲が 0 で (3,3)と(5,5) 位置の二点だけを 2 と 3 に設定しているだけと単純なときとしたので、ワンライナーで書けました。一般の より複雑な境界条件のときは、普通の python script として書くべきです。
N=10;dctB ={};for idx in mrng(N,N):dctB[idx]=True;dctB[3,3]=2;dctB[5,5]=3;plot3dRowCol( solveLaplacian(dctB) )
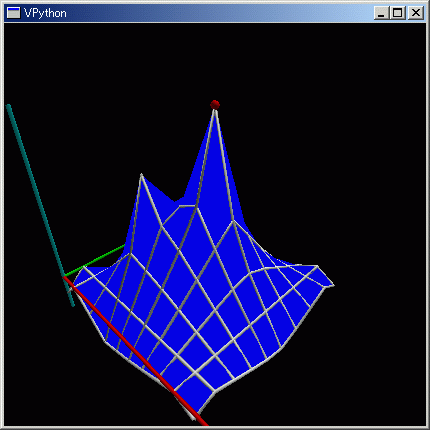
こんな単純な例でも、幾つかの境界条件で解いてみると、二次元でのラプラス偏微分方程式の解はゴム膜を引っ張ったときの配置に似ていることが解ります。
solveLaplacian(.) 関数の他に、偏微分方程式の数値的な解を求める汎用的な solver:solvePDE(..), itrSlvPDE(..) 関数を sf モジュールに用意しています。これらを使いこなすには、少しばかり勉強が必要になりますが、こちらにも挑戦してみてください。
sympy を使えば、抽象段階での数式処理が可能です。Python sf では sfCrrntIn.py の中で sympy モジュール名に ts の名前を割り振ってあります。
ts.factor(`x^4 + `x^2 + 1) =============================== (1 + x + x**2)*(1 - x + x**2) ts.factor(`x^4 + `x^3 + 1) ts.factor(`x^2 + `x + 1) =============================== 1 + x + x**2 ts.factor(`x^2 -1) =============================== -(1 + x)*(1 - x)
チャーチ数はλ計算によって自然数を定義するものです。λ計算を説明してある計算機科学の理論の本には、たいてい乗ってます。
でも、私は教科書ではチャーチ数が理解できませんでした。話が抽象的になりすぎているためです。でも、ここでのように python sf を使って具体的なチャーチ数を計算させてみたら、そんなに難しい話ではありませんでした。ペアノの自然数の公理系をλ計算で表現しただけのものでした。
具体的に考えてみましょう。Z = '1' 文字列とし、λs を s+'1' と文字列'1' を継ぎ足す操作としたとき、チャーチ数 2 は次のように定義されます。
Z='1';S =λ s:s+'1';(λ s:λ z:s(s(z)))(S)(Z) =============================== 111
Z='1';S =λ s:s+'1';(λ s:λ z:s(s( s(s(s(z))) )))(S)(Z) =============================== 111111
私の読んだλ計算の教科書:「ラムダ計算入門:1:7:3 自然数」ではλs や λz が天下りで与えられるだけであり、それらの式の意味を理解できませんでした。ここでのように具体例を計算させてみて、やっとλs の 's' が successor を意味しているのだと分かりました。
上の計算で λ を lambda に置き換えても同様な計算をさせられます。でも lambda と長い文字列を使って書いていたのでは、λ計算の意味が分かり難くなってしまいます。lambda 文字を λ 文字の置き換える Python sf プリプロセッサの威力を示す好例だと思います。
大多数の方が誤解していると思うのですが、Mathematica は数学のプロフェショナル向けのツールです。自分で科学分野での定理や公式などを作りあげる方たちのツールです。すでに出来上がっている定理や公式を使う物理学者やエンジニアたちが Mathematica を使うといっても、その機能のほんの一部分、グラフ機能などを使っているにすぎません。
そしてから大部分の物理学者・エンジニアたちが必要とする機能は scipy や sympy だけで、殆ど実現されています。Python sf は scipy や sympy の機能を使いやすくしているにすぎません。
でも python sf は scipy や sympy の機能を十二分に使いやすくしたとも自負しています。皆様の意見を伺わせていただけますでしょうか。
user の好きなように拡張できる意味では python sf が断トツだと主張します。 <== Octernion, GF(2^8) クラスを用意しました tnRcGn で無限再帰を可能にする generator ルーチンと itertools の改良版を用意しました。Haskell 以上でのような無限数列の記述を可能にしました。 <== python の duck typing により、python sf プリプロセッサが そのまま使えます。四則演算とべき上演算記述が後で追加している tnRcGn の Cocternon クラス・インスタンス GF(2^8) クラス・インスタンスについても適用できます。 <== sf python とは独立したモジュールとして python sf に追加して使っていますが、これらは python sf とは無関係に、単独のライブラリとしても利用できます。 <== 同様な python モジュールは、少し python ルーチンを書けるユーザーならば簡単に記述できるようになでしょう。