数学セミナー 2005 5 月号で
数列 {p[n]} が漸化式 p[n] p[n+1] = (n+1)/n の形式で定義されているとき、
数列 {p[n]} が単調減少になる初期値を p[0]を求めよ
との問題が出されました。それを sf を活用して解いてみました。
答えは π/2 です。出題者の意図は π/2 を見出すことと同時に、π/2 のときに限って、この数列が発振しなくなることを厳密に証明させたいのだと思います。残念ながら私の能力では厳密な証明はできませんでした。
でも、sf を使って数値的に π/2 であることを見つけられました。工学的/物理的/数値計算的には、これで充分な回答だとも考えます。私のような数学的センスが限られた人間でも、短い時間で π/2 の結論に到達できた解法であることは、純粋数学的な証明よりも優れた面を持っているとも言えます。工学的にはエレガントな解答であると主張します。
この意味で問題の解 π/2 に到達するまでの考察の過程を書いてみます。
問題の様子見として、初期値 p を 1 として与えられた漸化式でどんな数列になるか見てみます。
p@=1, N@=100, <<1,N,1 @k| p|, p=1/p (k+1)/k>>
< 1, 2, 0.75, 1.77778, 0.703125, 1.70667, 0.683594,
1.67184, 0.672913, 1.6512, 0.666183, 1.63755, 0.661557, 1.62786,
0.658182, 1.62063, 0.655611, 1.61502, 0.653587, 1.61054, 0.651953,
1.60689, 0.650606, 1.60385, 0.649477, 1.60129, 0.648516, 1.59909,
0.647689, 1.59719, 0.646969, 1.59553, 0.646337, 1.59406, 0.645778,
1.59276, 0.64528, 1.5916, 0.644833, 1.59055, 0.64443, 1.58961,
0.644065, 1.58875, 0.643732, 1.58796, 0.643428, 1.58724, 0.643149,
1.58658, 0.642891, 1.58597, 0.642654, 1.58541, 0.642433, 1.58488,
0.642228, 1.5844, 0.642038, 1.58394, 0.641859, 1.58351, 0.641692,
1.58312, 0.641536, 1.58274, 0.641388, 1.58239, 0.64125, 1.58206,
0.641119, 1.58174, 0.640995, 1.58145, 0.640878, 1.58116, 0.640767,
1.5809, 0.640662, 1.58064, 0.640562, 1.5804, 0.640466, 1.58017,
0.640376, 1.57996, 0.640289, 1.57975, 0.640206, 1.57955, 0.640127,
1.57936, 0.640052, 1.57917, 0.639979, 1.579, 0.63991, 1.57883,
0.639843, 1.57867 >
gdsp
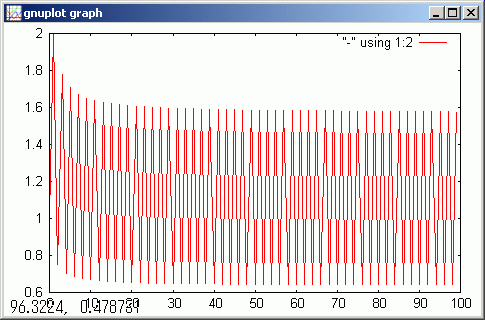
この漸化式は振動しやすいもののようです。p[n+1] = 1/p[n](n+1)/n また n+1/n > 1 ですから、数列要素が 1 より小さくなると発振します。初期値が 1 でも 2 でも発信します。どうも、この間に発振しない初期値がありそうです。
[1,2] の間を 100 等分した値それぞれを初期値とし、10 まで計算した数列ベクトルを縦にならべた行列を計算してみます。
//@@
N @=100
mt = <<1,N, 1/N @ p0 |\
temp = p0
<<1,10,1 @ k|\
temp|, temp= (k+1)/k 1/temp
>>
>>
//@@@
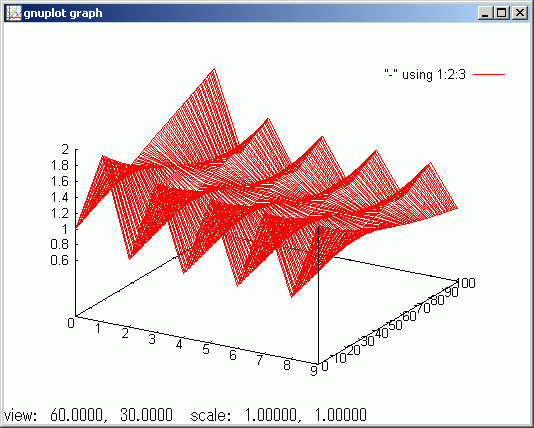
gspl mt
gspl は行列変数 mt の index i, j を x,y 座標位置として、行列要素の値を z 値として三次元表示させます。この場合は 100 x 10 行列 mt を表示させています。x,y 軸は行列の index 値であり整数値に限定されます。[1,2] の範囲を 100 等分しているので x 軸は 1 から 2 の範囲にあるべきなのですが、下の gnuplot 3D 画像では 0 から 100 の x 軸になってしまっています。
でも、計算している本人は 0 から 100 の範囲は 1.0 から 2.0 を 100 当分したことは解っています。計算している本人とっては x 軸が 0 から 100 の下図のグラフでも困りません。それよりも試行錯誤している段階では、 "gspl mt" の単純なマンドだけで表示してくれるほうが便利です。set x_range start, end などのパラメータを設定に手間をかけていては、思考の速度に操作が追従できません。このような、一見手抜きのグラフ表示のほうがユーザーに負担をかけずに済みます。論文などで読者の読みやすさを重視したグラフにするためには python の matlab 互換表示を使います。

このグラフを見ていると、1 と 2 の間で一つの上手い初期値を取ってやると発振せずに済みそうです。このグラフはマウスでドラッグすることにより視点を変えられます。真横から見てみます。
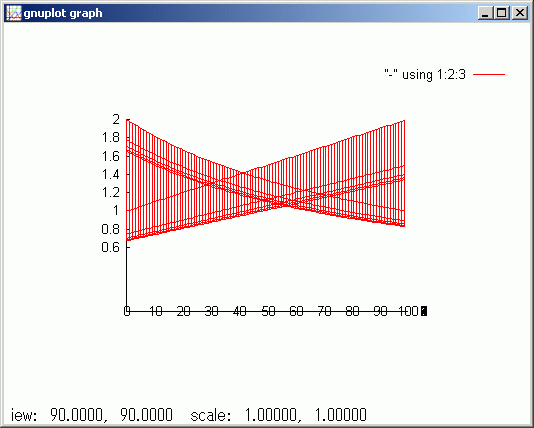
どうも [1.5, 1.6] の間の適当な値を初期値としたとき発振しないようです。その値は一つだけのようです。
今一度漸化式に戻って,初期値 p に対する数列 {p[n]} の一般式を求めてみます。
初期値 p
二回目の値 1/p (1+1)/1
三回目の値 (1/p (1+1)/1)^-1 (2+1)/2 == p 1/(1+1) (2+1)/2
四回目の値 (p 1/(1+1) (2+1)/2 )^-1 (3+1)/3
== 1/p (1+1)/1 1/(2+1) (3+1)/3
2n+1 回目の値
1 3 ... (2n-3) (1+1)(3+1) ... (2n-2)
p ------------------------ ( ---------------------- )^-1
2 4 ... (2n-2) (2+1)(4+1) ... (2n-1)
( (2+1)(4+1) ... (2n-3) )^2
== p ------------------------------- (2n-1) -------(式 1)
( (1+1)(3+1) ... (2n-2) )^2
2n 回目の値
2 4 ... (2n-2)
1/p 2n (-------------------------)^2
1 3 ... (2n-3)(2n-1)
2 4 ... (2n-4)(2n-2)
== 1/p 2n (-------------------------)^2 ------------(式 2)
3 5 ... (2n-3)(2n-1)
数列 {p[n]} が単調減少のためには、(式 1)と(式 2) どちらも 1 に漸近していく必要があります。(式 2) には 1/p の項が入っているので、(式 2) の極限が 1 になることより
n-1
p = lim 2 n Π(2k/(2k+1))^2 -------------(式 3)
n->∞ k=1
が成り立つはずです。下の計算で単調減少になる初期値 p が決まります
p=( n@=1000, 2n !prdct(<<1, n-1,1 @ k | 2k/(2k+1)>>)^2 )
< 1.57119 >
単調減少になる初期値を三桁の精度に求めた上の計算でも、工学的には充分な場合が多いはずです。
積級数では扱い難いので log をとって足し算にしてみます
n-1
log(p) == log(2 n Π(2k/(2k+1))^2 )
k=1
n-1
== log(2n) + 2Σ(log(2k) - log(2k+1))
k=1
2n ∫ 1/x dx = log(2n) 1 1+2(k+1) ∫ 1/x dx = log(1+2(k+1)) - log(1+2k) 1+2kですから下の (式 4) が成り立ちます。
n-1
log(p) == log(2n) + 2Σ(log(2k) - log(2k+1))
k=1
n-1 1+2(k+1)
== log(3)-log(1) + Σ( ∫ 1/x dx + 2 log(2k/(2k+1))
k=1 1+2k
n-1
== log(3) + Σ ( log(1+2(k+1)) - log(1+2k) + 2 log(2k)- 2log(2k+1) )
k=1
n-1
== log(3) + Σ ( 2 log(2k)- 3 log(2k+1) + log(2k+3) ) -------(式 4)
k=1
(式 4) を使って数列 {p[n]} が単調減少になる初期値 p を計算します。
p= !exp(n@=10000,/s,!log(3)+!sum(<<1,n-1, 1 @k| 2!log(2k)- 3!log(2k+1) +!log(2k+3)>>) ) < 1.570914138974103 > # より高精度に p を求めるため 40000 回まで増やしてみます p= !exp(n@=40000,/s,!log(3)+!sum(<<1,n-1, 1 @k| 2!log(2k)- 3!log(2k+1) +!log(2k+3)>>) ) < 1.570825779380696 >
この初期値 p に対する数列 {p[n]} の単調減少の様子を確認してみます
temp = p, <<1,128,1 @ k| temp|, temp= (k+1)/k 1/temp >> < 1.57083, 1.27322, 1.17812, 1.13175, 1.10449, 1.08648, 1.07381, 1.0643, 1.05703, 1.05116, 1.04646, 1.04248, 1.03919, 1.03631, 1.03389, 1.0317, 1.02985, 1.02813, 1.02667, 1.02529, 1.02411, 1.02296, 1.02199, 1.02103, 1.02022, 1.01939, 1.01871, 1.01799, 1.01741, 1.01678, 1.01628, 1.01573, 1.01528, 1.01479, 1.01441, 1.01396, 1.01362, 1.01322, 1.01292, 1.01256, 1.01229, 1.01196, 1.01171, 1.01141, 1.01119, 1.01091, 1.01071, 1.01045, 1.01027, 1.01003, 1.00987, 1.00964, 1.0095, 1.00928, 1.00915, 1.00895, 1.00883, 1.00864, 1.00853, 1.00835, 1.00825, 1.00808, 1.00799, 1.00782, 1.00774, 1.00759, 1.00751, 1.00736, 1.00729, 1.00715, 1.00709, 1.00695, 1.00689, 1.00676, 1.00671, 1.00658, 1.00653, 1.00641, 1.00637, 1.00625, 1.00621, 1.0061, 1.00606, 1.00595, 1.00592, 1.00581, 1.00578, 1.00568, 1.00565, 1.00555, 1.00553, 1.00543, 1.00541, 1.00531, 1.0053, 1.0052, 1.00519, 1.0051, 1.00508, 1.00499, 1.00498, 1.0049, 1.00488, 1.0048, 1.00479, 1.00471, 1.0047, 1.00462, 1.00462, 1.00454, 1.00453, 1.00446, 1.00445, 1.00438, 1.00438, 1.0043, 1.0043, 1.00423, 1.00423, 1.00416, 1.00416, 1.00409, 1.00409, 1.00402, 1.00403, 1.00396, 1.00396, 1.0039 >
gdsp
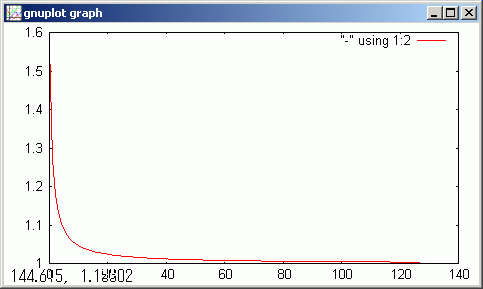
グラフでは分かりませんが最後のほうで ... 1.00409, 1.00402, 1.00403, 1.00396 ... と 6 桁目で単調減少が破れたことが数値的に解ります。
p の値を眺めていると、その値が π/2 に近い事に気付きます。
/p 16,`π/2- p < -2.945258579933885e-005 >
6 桁の精度で π/2 です。たぶん最初の設問の正しい答えは π/2 でしょう。出題者の意図は 数列 {p[n]} が単調減少となる初期値は π/2 ことを見つけ出すとと、それが π/2 であることの数学的に厳密な証明をさせる点にあると思います。
残念ですが私の数学能力では(式 4) が π/2 に厳密に収束することの証明ができません。積分式に結び付けるために (式 4) を導いたのですが、ここで行き詰まっています。
しかし私のような数学センスのない人間でも sf を使うことで、「数列 {p[n]} を単調減少させる初期値は π/2 である。」との結論までには到達できました。答えの半分は得られました。与えられた問題の文章を眺めているだけでは、また数式を闇雲に変形しているだけでは、この結論に到達できなかったと考えます。また C などのコンピュータ・プログラムで力任せに計算させようとしてもプログラムのデバッグ作業の泥沼に嵌るだけだったと思います。
物理や工学の分野ならば、6 桁の精度で π/2 であることを知る事ができただけでも充分だとも考えます。それが sf コンピュータ計算による結果であり、私のような数学センスのない人間でも π/2 の結論には到達できたことは誇ってもよいと考えます。物理的/工学的/数値計算的にはエレガントな解答だと考えます。
たぶん π/2 が数列を振動させないことを証明するためには (式 4) の変形ではなく、上手い π/2 による数列表示モデルを提示することが出題者の意図だろうと推測しています。でも π/2 が高い確率で唯一の解だと解ってしまうと、これを厳密に解くモチベーションが保てなくなってしまいました。物理/光学系の人間ならばこれで許されると考えます。
天才的な暗算能力により数学の発展に貢献したインドのラマヌジャンは、ここで行ったような計算を頭の中だけで行っていたのだと思います。現在の我々はコンピュータと sf を使うことでラマヌジャンと同等以上の計算能力を持てるとも思います。このような sf を知ってもらいたくて、この web ページを書いています。皆様も sf を是非ダウンロードしてお試し下さい。