
現在のコンピュータ パワーを活用して解析関数がどのような形をしているのかをコンピュータ画面上にカラー表示します。
kkRGB.exe を使って複素数値の四次元分布をカラー表示させます。解析関数の複素数値分布は sf や python を使って計算させます。コンピュータ パワーを活用して sin(z) などの解析関数がどんな複素数値分布をしているのか見ていきます。
できましたら、皆様も御自分のコンピュータ上で計算させながら、自分で関数の種類や値域を設定し、複素数分布を計算させ、mkRGB.exe を使って表示させながら読んでいかれることを希望します。そのほうが面白いはずです。sf や mkRGB.exe はこちらからダウンロードできます。python は Enthought パッケージが、こちらからダウンロードできます。
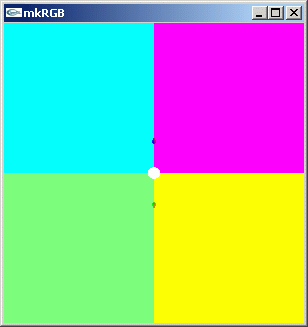
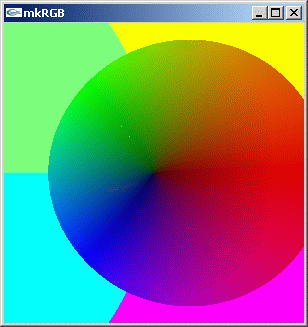
コンピュータの RGB 表示をを活用して、二次元平面上に複素数変面上での複素数分布を表示させることを提案します。下に 0+0i を中心とする複素平面上の複素数値と、RGB ピクセルの対応させ方を表す「複素数値 kkRGB 地図」を示します。

mkRGB.exe は sf 複素行列変数ファイルを変換して、kkRGB 図として表示させるプログラムです。100 x 200 sf 複素数行列ファイル名を引数に与えたとき、mkRGB.exe は 100 pixel 幅で 200 pixel 高さの二次元画面に表示します。個々の pixel は sf 複素行列変数の i,j 複素数値を「複素数値 kkRGB 地図」に従って RGB の色に変換し、横 i pixel, 縦 j pixel の位置に表示させます。
複素数変面上での複素数分布のデータは四次元データになります。複素関数を紙の上の図形して表示するためには、実数値の分布と虚数値の分布の二つに分けて表示する必要がありました。実数値と虚数に分けてしまうと位相の変化が分かりにくくなってしまいます。 結局、複素関数値が複素平面状でどのように分布しているのか、どのように位相が回転しているのか明確にイメージできないままでした。
mkRGB.exe を使うことで、一つの kkRGB 図に複素数値の分布を表示させることができます。解析関数の複素数値分布を直感的に把握できる形式で表示できます。
mkRGB.exe はこちらに置いてある sf12b.zip の中にあります。解凍してお使いください。
mkRGB に与える sf 複素行列変数ファイルは sf または python で作ります。
sf による sf 複素行列変数ファイルの生成は sf の二重ループによって行列を生成することで行います。100x100 の sf 行列変数ファイルは、以下のような具合に作れます。
//@@
/s
xLeft @= -1.0
Δx @= 2.0
yUpper @= 1.0
Δy @= 2.0
N@=100
temp=<< xLeft+Δx/(2N),N, Δx/N @ x, _j|\
<< yUpper-Δy/(2N),N, -Δy/N @ y, _k|\
!sin( (x+y i)**2 )
>>
>>
//@@@
python まで勉強してられないときには、10 倍の計算時間が必要ですが、sf で解析関数の複素行列変数ファイルを作成してください。
python を使えば、sf よりも高速に sf 行列変数ファイルを作成できます。zeta 関数など、より広い範囲の解析関数を対象とできます。
下のような sf 複素数値行列変数ファイルを作るモジュールを使います。カレント ディレクトリに dpAnltc.py を作り、下のブロックの python code をコピー&ペーストして下さい。sfVal.py が必要となるのでこちらからダウンロードください。
# type dpAnltc.py
from scipy import reshape, zeros, log, arange, Complex64
import sfVal
def dumpFnctn(fAg,xNag=100, yNag=100, xLeftAg = -1.5, xRightAg=1.5, yUpAg = 1.5, yDownAg = -1.5):
matrix=reshape( zeros(xNag*yNag, Complex64), (yNag,xNag) )
for (real,n) in zip(arange(xLeftAg+(xRightAg-xLeftAg)/(2*xNag)
,xRightAg,(xRightAg-xLeftAg)/xNag),range(xNag)):
for (image,m) in zip(arange(yUpAg-(yUpAg-yDownAg)/(2*yNag)
,yDownAg,-(yUpAg-yDownAg)/yNag),range(yNag)):
#print 'sAg:', (real,image), ' m:',m, " n:",n," ",matrix[m,n]
matrix[m,n] = fAg(real + image*1j)
print n
sfVal.putSf(matrix, 'mtCplx')
def dumpLogFnctn(fAg,xNag=100, yNag=100, xLeftAg = -1.5, xRightAg=1.5, yUpAg = 1.5, yDownAg = -1.5):
matrix=reshape( zeros(xNag*yNag, Complex64), (yNag,xNag) )
for (real,n) in zip(arange(xLeftAg+(xRightAg-xLeftAg)/(2*xNag)
,xRightAg,(xRightAg-xLeftAg)/xNag),range(xNag)):
for (image,m) in zip(arange(yUpAg-(yUpAg-yDownAg)/(2*yNag)
,yDownAg,-(yUpAg-yDownAg)/yNag),range(yNag)):
#print 'sAg:', (real,image), ' m:',m, " n:",n," ",matrix[m,n]
zetaAt = fAg(real + image*1j)
absAt = abs(zetaAt)
logAt = log(1+absAt)
matrix[m,n] = logAt * zetaAt / absAt
print n
sfVal.putSf(matrix, 'mtCplx')
どちらの関数も、最初の引数に求めたい解析関数を指定します。二番目に行列の行サイズを指定します。kkRGB 表示の横 pixel 数と同じです。三番目に行列の列サイズを指定します。kkRGB 表示の縦 pixel 数と同じです。計算させる値息は複素平面の四角形です。四番目に四角形の左端の実数値を指定します。五番目に四角形の右端の実数値を指定します。六番目に四角形の上端の虚数値を実数値で指定します。七番目に四角形の下端の虚数値を実数値で指定します。下のような具合です
//@@ from scipy.special import sin from dpAnltc import * dumpFnctn(lambda z:sin(z**2), 300,300,-1.0,1.0, 1.0, -1.0) //@@@指定された関数の mtCplx.val という名前の複素数値 sf 行列ファイルを生成します。 それを使って mkRGB mtCplx -max:0.5 などと kkRGB 表示させます。
デフォルト引数のパラメータが設定されています。デフォルトでは 300 dot x 300 dot の pixel 数で [-1.5,1.5] x[1.5,-1.5] の領域の複素数分布を計算します。
関数 f(z) が解析関数であるとき、f(z) は複素平面を定義域とし、また値粋とします関数です。z ∈ Complex & f(z) ∈ Complex です。解析関数 f(z) は特異点を除いて複素平面での微分が可能です。f(z) の微分を計算するとき Δz→0 のさせかたは実数関数のときより多くなります。そして解析関数 f(z) は
limit (f(z0+Δz) - f(z0) )/Δz Δz→0
具体例を考えます。sin(z) を 1+2i の位置で微分して見ます
//@@
# 実数軸の方向で Δz→0 操作を行う
z0 = 1+2i
N @= 6
θ @= 0
r @=0.1
<<1,N,1@j|\
r = r/10
Δz @= r!exp(iθ)
z@= z0 + Δz
( !sin(z0+ Δz) - !sin(z0) )/Δz
>>
//@@@
< 2.01686-3.06164i, 2.03114-3.05288i, 2.03256-3.052i, 2.03271-3.05191i
, 2.03272-3.0519i, 2.03272-3.0519i >
//@@
# 虚数軸の方向で Δz→0 操作を行う
z0 = 1+2i
N @= 6
θ @= `π / 2
r @=0.1
<<1,N,1@j|\
r = r/10
Δz @= r!exp(iθ)
z@= z0 + Δz
( !sin(z0+ Δz) - !sin(z0) )/Δz
>>
//@@@
< 2.04255-3.06778i, 2.0337-3.05348i, 2.03282-3.05206i, 2.03273-3.05191i
, 2.03272-3.0519i, 2.03272-3.0519i >
//@@
# 右斜め上から Δz→0 操作を行う
z0 = 1+2i
N @= 6
θ @= `π / 3
r @=0.1
<<1,N,1@j|\
r = r/10
Δz @= r!exp(iθ)
z@= z0 + Δz
( !sin(z0+ Δz) - !sin(z0) )/Δz
>>
//@@@
< 2.03327-3.07056i, 2.03278-3.05376i, 2.03273-3.05208i, 2.03272-3.05192i
, 2.03272-3.0519i, 2.03272-3.0519i >
!cos(1+2i)
< 2.03272-3.0519i >
解析関数が複素平面上で微分可能であることは、結構強い制限です。制限によって解析関数の美しい構造が導かれます。
∂f(z).real/∂z.real == ∂f(z).image/∂z.image = ∂f(z).image/∂z.real == -∂f(z).real/∂z.image =
∂f.real(x,y)/∂x - ∂f.image(x,y)/∂y == 0 ∂f.image(x,y)/∂y - ∂f.real(x,y)/∂x == 0
逆に特異点を含む二点間の積分路の差は常に一定です。解析関数の二点間の積分路の値は、特異点によって決まってしまうとも言えます。詳細は数多くの web page 教科書を参照ください。
sf での数値実験を!解析関数の勉強をするとき、上の解析関数の微分で行ったような数値実験を行うことをすすめます。sf を使えば二点間の数値積分なぞ簡単に行えます。数値実験をしながら解析関数を勉強をしていくことで、数式だけを追っていくときよりも、より深く理解できます。無用な誤解をせずに済みます。
kkRGB.exe の引数に与える sf 複素行列ファイル変数は単なるテキスト・ファイルです。sf での計算式の対象とするために定義されました。sf や sfVal.py の puSf(.) 関数で出力させれば、自動的に sf 複素行列ファイル変数のフォーマットで出力されます。 でも、このフォーマットを満たせば、他のプログラムから sf 複素行列ファイル変数を作り mkRGB.exe に kkRGB 表示させることも可能です。
このフォーマットを説明します。下に 5 x 2 の複素行列の sf ファイルの中身を例示します。
type mt.val % BaseComplexDoubleMatrix 5, 2 < -1.010875342582172e+065 +4.234147225207233e+064i, 1.657203572139946e+064 -5.008606545684682e+064i > < -2.254936183883746e+064 +2.884564265820551e+064i, 6.588785106281863e+064 +1.81483395600486e+065i > < -3.307555463112328e+065 -1.96425291809001e+065i, 7.105114280752834e+064 -1.428343444730398e+064i > < 8.538161848811448e+065 -2.761038788587805e+065i, -5.173337738213509e+063 +5.368918136753312e+064i > < 1.08593238674481e+065 +1.128163816105048e+064i, -3.698440760957881e+065 -1.867966326505306e+065i >
最初の行の「% BaseComplexDoubleMatrix」は複素行列を示す文字列であり、そのまま出力してやらねばなりません。次の「5, 2」は、このファイルが 5 x 2 行列であることを宣言しています。スペースの入れ方は自由ですが 「,」を忘れないで下さい
二行目からが行列データです。行列の一行データを書き出して、最後に改行が追加されます。
< -1.010875342582172e+065 +4.234147225207233e+064i, 1.657203572139946e+064 -5.008606545684682e+064i >
この各行の < スペース コンマや > の記号や数値文字列の長さは同じフォーマットにする必要があります。次の規則を守って行データを文字列に変換してください。
以上のフォーマットを守って sf 複素行列ファイル作るならば、どんなプログラムによって長方形の複素数値分布データを作っても mkRGB.exe で表示させられます。
以下では解析関数の概要は知っているものとして、具体的な解析関数の複素数値の分布、位相回転の様子を kkRGB 表示する事で見ていきます。知ってるつもりの基本関数でも意外な性質が見えてきます。
まず最も単純である多項式の複素数値分布を見てみましょう。z^2 と z^5+2*z^4+3*z^3+4*z^2+5*z+6 の二つの多項式です。
//@@
/s
xLeft @= -1.0
Δx @= 2.0
yUpper @= 1.0
Δy @= 2.0
N@=100
temp=<< xLeft+Δx/(2N),N, Δx/N @ x, _j|\
<< yUpper-Δy/(2N),N, -Δy/N @ y, _k|\
z @= x+y i
# 下の行の関数形を変えてやることで任意の複素関数の値分布を計算できる
z^2
>>
>>
//@@@
//@@ from dpAnltc import * dumpFnctn(lambda z:z**2, 300,300,-1.0,1.0, 1.0, -1.0) //@@@
この dumpFnctn(.) python 関数は z^2 の複素数分布データを mtCplx.val の名前の sf 行列変数ファイルに入れています。それを下のように mkRGB で表示させます。
mkRGB mtCplx -max? Maximum:1.98669 Column:0 Row:0 mkRGB mtCplx -max:0.1 -limit:5
-max:0.1 オプションはアナログ RGB 表示の最大値を mtCplx 行列の最大値の 0.1 倍にすることを意味します。三色の RGB を連続して混ぜ合わせるアナログ RGB 表示領域と、橙色/黄色/緑色/空色の四色のみの組み合わせで表示するデジタル RGB 領域の境界が 1.98669 * 0.1 == 0.19867 であることを意味します。-limit: オプションはデジタル RGB 表示領域と白領域との境界値を -max: 値からの倍率で設定します。この場合は 0.19867*5 == 0.99335 が、その境界における絶対値になっています。
左側の kkRGB 図形は z^2 の複素数値分布を示します。kkRGB 表示をさせているとき r キーを押すと、ピクセル値を 1/z で計算しなおした図形を描かせた右側の kkRGB 図形に換えます。右側の reversed kkRGB 図は 1/z^2 == z^-2 の複素数分布だとも言えます。
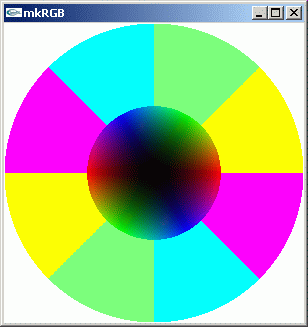
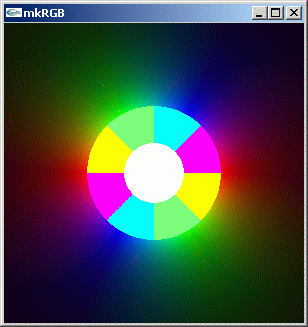
0+0i を中心に定義域を一周すると z^2 の位相は二回転、即ち 4π 回転することが解ります。z^2 は 0+0i を最小とし、そこからの距離が大きくなるほど関数値の絶対値も大きくなることが分かります。解析関数の複素数値分布の概要を kkRGB 図から読み取るとき、四色で表示されるデジタル RGB 領域が一番役立ちます。境界が明確だからです。-max: -limit: オプションの値を設定しなおしてやる事で、より細かく関数値の分布を調べられます。
z^2 よりも複雑な、重根ではない五次の多項式 z^5+2z^4+3z^3+4z^2+5z+6 の複素数値分布を求めます。
//@@ from dpAnltc import * dumpFnctn(lambda z:z**5+2*z**4+3*z**3+4*z**2+5*z+6, 300,300,-3.0,3.0, 3.0, -3.0) //@@@
この dumpFnctn(.) python 関数は z^2 の複素数分布データを mtCplx.val の名前の sf 行列変数ファイルに入れています。それを下のように mkRGB で表示させます。
mkRGB mtCplx -max? Maximum:1874.06 Column:0 Row:299 mkRGB mtCplx -max:0.01
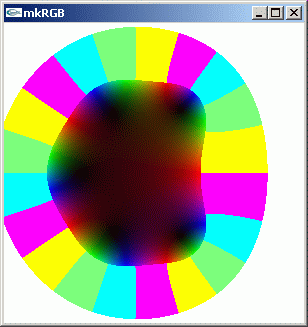

右側の kkRGB リバース図の白い点が根のある位置です。このゼロ点の周りで位相が一回転していることが分かります。左側の kkRGB 図より、この多項式を 0+0j から 3 程度離れた領域からみると、位相が 10 回転しており z^5 に近くなってきていることも解ります。
上の五次多項式の実根を 0+0i の位置に移してやります。根の位置の変化に伴って位相回転がどのように変化するかを見てみましょう。
//@@
from dpAnltc import *
dumpFnctn(lambda z:(z**4 + 0.5082*z**3 + 2.242*z**2 + 0.6556*z + 4.022)*z
, 300,300,-3.0,3.0, 3.0, -3.0)
//@@@
mkRGB mtCplx -max:0.01
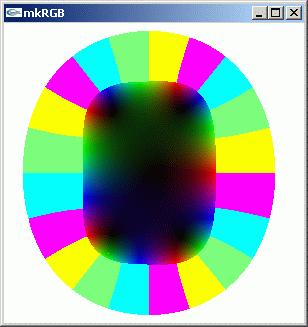

z の非整数乗の関数では、原点の周りで位相が整数回転できません。多価関数となります。
z^(1/2) の複素数分布を kkRGB 表示します。デフォルト パラメータを使うので 300 dot x 300 dot の pixel 数で [-1.5,1.5] x[1.5,-1.5] の領域の複素数分布を計算します。
//@@ from dpAnltc import * dumpFnctn(lambda z:z**0.5) //@@@
mkRGB mtCplx -max? Maximum:1.45405 Column:0 Row:0 mkRGB mtCplx
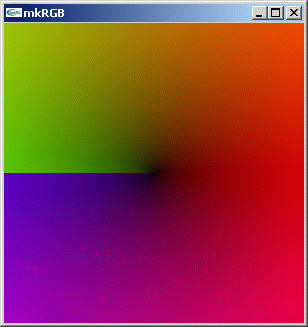

複素平面上で原点を中心に 1/2 回転しています。 左側のノーマル kkRGB 図で、負の実数軸で位相が不連続になっています。リーマン面です。関数は多価関数となります。らせん状に積み重なっています。
リーマン面が負の実軸になっているのは多価関数の計算上の都合です。
//@@ from dpAnltc import * dumpFnctn(lambda z:z**3.3) //@@@
mkRGB mtCplx -max? Maximum:11.8308 Column:0 Row:299 mkRGB mtCplx -max:0.1
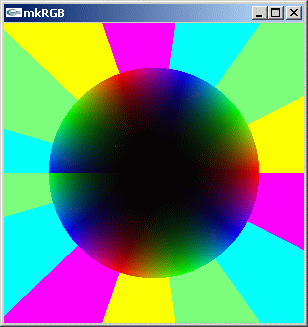
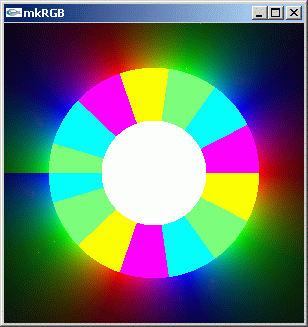
z^3 と良く似た kkRGB 図になります。原点の周りの位相回転が 3 回転より 0.3 回転だけ増えます。位相の不連続点が出てしまいます。負の実数軸が、この不連続点として表示されています。リーマン面です。z^3.3 は多価関数になってしまいました。
exp(z) == e^z の複素数値分布を見てみましょう。定義域を広げて、関数値の変化の様子をより分かり安くします。
//@@ from scipy.special import exp from dpAnltc import * #dumpLogFnctn(lambda z:exp(z),300,300,-5.0,5.0,5.0,-5.0) dumpFnctn(lambda z:exp(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:145.96 Column:91 Row:299 mkRGB mtCplx -max:0.01

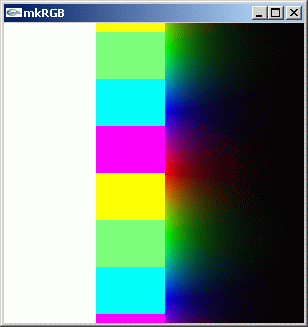
exp(z) は、虚数軸方向に対しては位相が変わるだけで絶対値が変化しないことが分かります。正の実数軸方向に移動すると、その絶対値は exp の指数カープで増加していくことも分かります。
//@@ from dpAnltc import * dumpFnctn(lambda z:5**z,300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:3042.29 Column:69 Row:299 mkRGB mtCplx -max:0.01
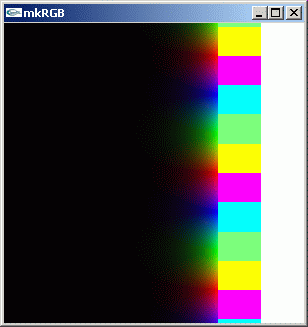

exp(z)より大きく変化するようになりますが、虚数軸方向に対しては位相が変わるだけで絶対値が変化しないことは同じです。正の実数軸方向に移動すると、その絶対値は 指数カープで増加していくことも同じです。
//@@ from dpAnltc import * dumpFnctn(lambda z:(3+4j)**z,300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:309090 Column:299 Row:299 mkRGB mtCplx -max:0.01
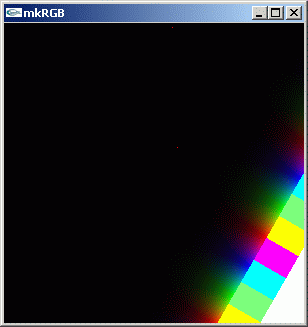
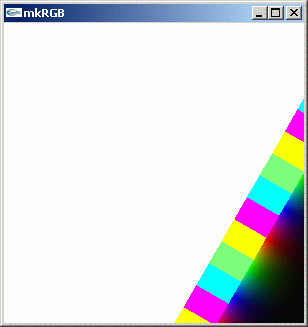
絶対値が一定となる等高線が傾くことが分かります。
嫌がらせとさえ思える z^z の複素数値分布を見てみましょう。皆様は z^z がどのような位相変化をしているか、z^z が複素平面上でどのような複素数値分布をしているか、それぞれイメージできますでしょうか。
//@@ from dpAnltc import * dumpLogFnctn(lambda z:z**z,300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:8.00403 Column:149 Row:299 mkRGB mtCplx -max:0.01
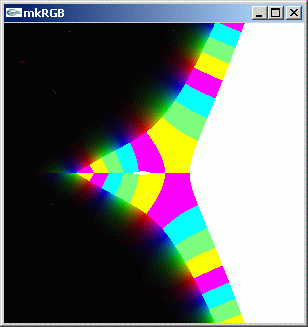
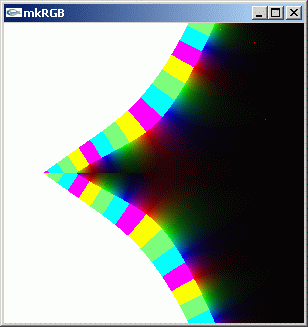
右側に行くにつれて急激に絶対値が大きくなる関数であることが一目で分かります。
境界値設定を 10 倍にしてやって、上の kkRGB 図で値が大きくなりすぎて白くなっている部分の位相変化を見えるようにしてみます。
mkRGB mtCplx -max:0.01
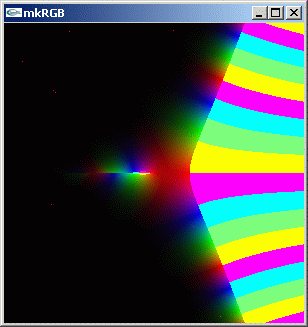
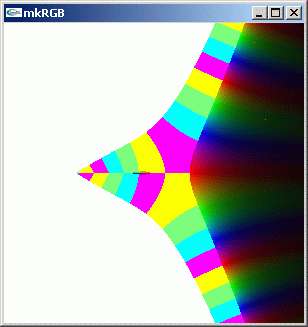
実数軸上で 0+0i の左側に小さなこぶががあります。その部分の絶対値の様子をグラフにして見ます。
!abs(mtCplx[149,*])
gdsp
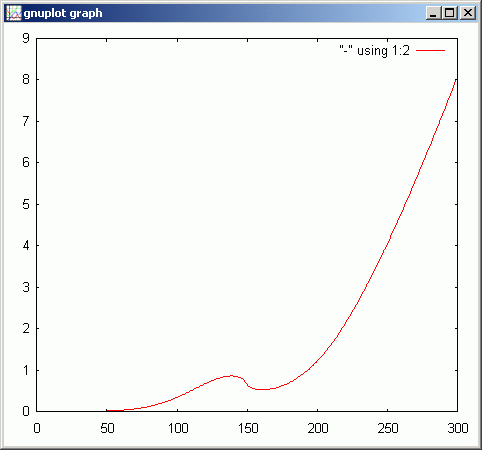
このこぶの部分だけに限定して kkRGB 図を拡大しましょう。実数:[-1,0] 虚数[0.5,-0.5] の上下、左右を 1/10 にまで絞った領域での複素数分布を見てみます。この領域では変動が小さいので log をとらずに計算させます。
//@@ from dpAnltc import * dumpFnctn(lambda z:z**z,300,300,-1.0,0., 0.5,-0.5) //@@@
mkRGB mtCplx -max? Maximum:1.43713 Column:149 Row:189 mkRGB mtCplx
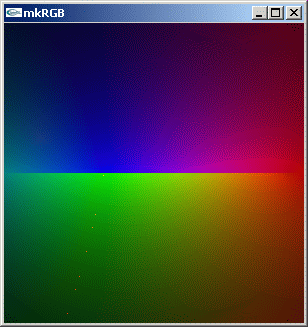

リーマン面は -1.0+0i から 0+0i の範囲だけではありません。-2+0i から 0+0i に kkRGB 図を拡大してみます。
//@@ from dpAnltc import * dumpFnctn(lambda z:z**z,300,300,-2.0,-0.0, 1.0,-1.0) //@@@
mkRGB mtCplx
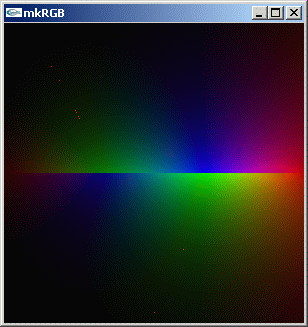
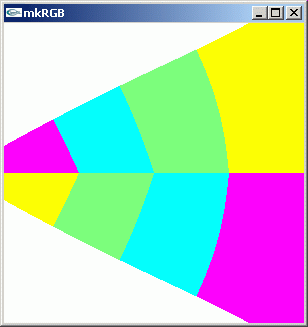
リーマン面での位相変化から、その切り口での多価関数の様子をイメージできます。上の kkRGB 図からは [-1+0i , 0+0i] の区間でチューブの断面のようになっている z^z 解析関数の断面がイメージできます。[-2+0i , -1+0i] の区間でも、別のチューブ断面構造が存在します。上下の離れ具合は [-1+0i , 0+0i] のときより小さくなっています。
この断面のチューブを解析接続して複素平面全体に広げてやることで z^2 の複素数値分布をイメージできます。z^z は二価関数でしょう。正の実数軸(橙色と黄色の境界)、負の実数軸(空色と緑色の境界)では、二価の関数で構成されるチューブが互いに接触して一価の関数となりそうです。そのチューブの曲がり具合は kkRGB 図の等位相面で分かります。
exp(z^2) 即ち多項式と exp() を組み合わせた解析関数の複素数値分布を見てみましょう。
//@@ from scipy.special import exp from dpAnltc import * dumpLogFnctn(lambda z:exp(z**2),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:24.8333 Column:149 Row:0 mkRGB mtCplx -max:0.05

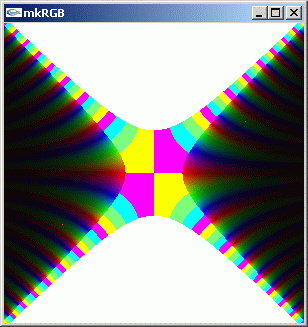
絶対値は左右対称で 0+0i から左右離れるにしたがって急激に大きくなります。上下にも対称です。0+0i から上下に離れるにしたがって急激に小さくなります。
上下だけではなく、左右にも共役です。この共役性は下のように数値計算でも確認できます。
z@=1+2i, !exp(z^2) < -0.032543-0.037679i > z@=-1+2i, !exp(z^2) < -0.032543+0.037679i > z@=1-2i, !exp(z^2) < -0.032543+0.037679i >
ちなみにエラー関数は exp(-z^2) == 1/exp(z^2) です。ですから、上の二つの kkRGB 図の左右を入れ替えてやれば、エラー関数の複素数分布とも見なせます。
//@@ from scipy.special import sin from dpAnltc import * dumpFnctn(lambda z:sin(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:72.9835 Column:0 Row:8 mkRGB mtCplx -max:0.01


上下方向に移動したとき、絶対値が急激に増加することが分かります。左右に移動したときは sin 関数と同様な位相変化をすることも分かります。絶対値の等高線は横一直線が少しだけ波打っていることが見てとれます。
//@@ from scipy.special import cos from dpAnltc import * dumpFnctn(lambda z:cos(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:72.9835 Column:0 Row:55 mkRGB mtCplx -max:0.01
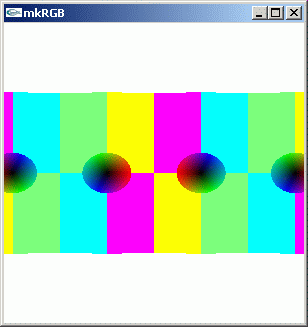

複素平面まで拡張したときでも、sin と cos の違いは位相変化が π/2 ずれていることが違うだけのようです。
//@@ from scipy.special import tan from dpAnltc import * dumpFnctn(lambda z:tan(z),300,300,-5.0,5.0,5.0,-5.0) #dumpLogFnctn(lambda z:tan(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:58.1213 Column:149 Row:291 mkRGB mtCplx -max:0.01

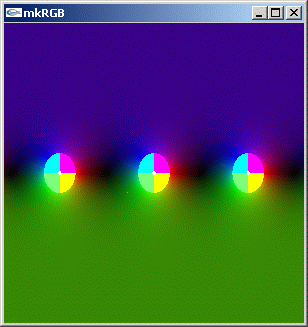
極は実数軸上にのみ存在するようです。sin/cos 関数のときと異なり、上側/下側それぞれで real part が正/負だけに限定されます。x 軸方向に移動させたとき tan(x) は複素平面でも πの周期性を持つことが見られます。
上下に移動しても tan(z) はあまり変動しないようです。境界値を 5 倍大きく設定した、下の kkRGB 図より、上下方向に垂直に移動させるとき一定の値に収束するのが解ります。
mkRGB mtCplx -max:0.05
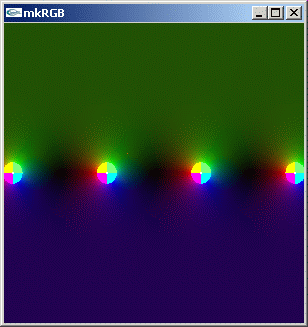

下のグラフより、上の kkRGB 図より上下方向の値の変化の仕方がより詳細にイメージできます。
!abs(mtCplx[*,149])
gdsp
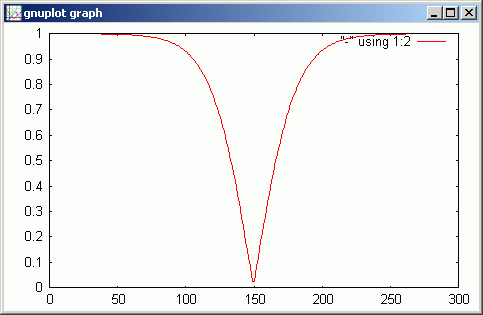
!image(mtCplx[*,149])
gdsp
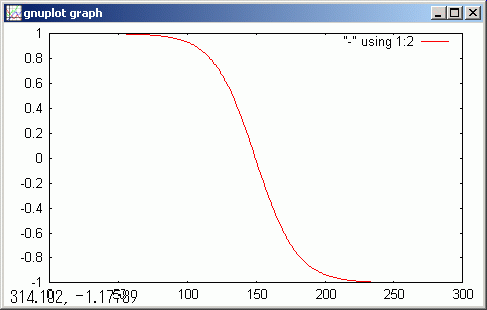
cot(z) は tan(z) と、どんな違いとなるのか見てみましょう。
//@@ from scipy.special import sin, cos from dpAnltc import * dumpFnctn(lambda z:cos(z)/sin(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:53.5738 Column:149 Row:244 mkRGB mtCplx -max:0.01

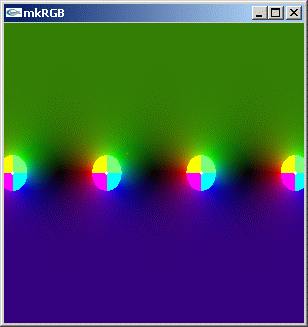
複素数の範囲でも、 cot(z) は tan(z) と実数軸方向に π/2 だけ位相がずれたものであると解ります。
三角関数の逆関数の複素数値分布を調べます。
asin(z) の複素数値分布を見てみましょう。
//@@ from cmath import asin from dpAnltc import * dumpFnctn(lambda z:asin(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:2.77423 Column:150 Row:0 mkRGB mtCplx -max:0.8

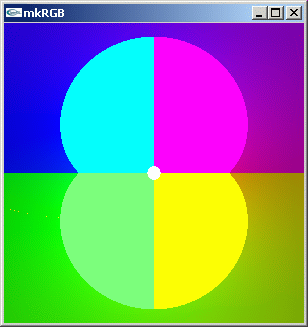
実数軸の -1+0i より左側と、 1+0i より右側にリーマン面が出てきました。リーマン面の始まる位置での変化をより詳しく見るため,実数:[-1.5,1.5] 虚数:[1.5,-1.5] に領域を狭めます。
//@@ from cmath import asin from dpAnltc import * dumpFnctn(lambda z:asin(z),300,300,-1.5,1.5,1.5,-1.5) //@@@
mkRGB mtCplx -max? Maximum:1.83602 Column:149 Row:0 mkRGB mtCplx mkRGB mtCplx -max:0.8
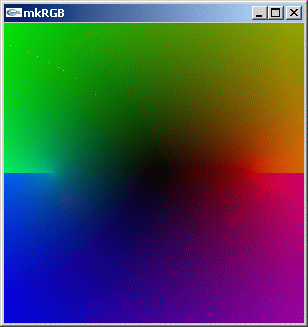
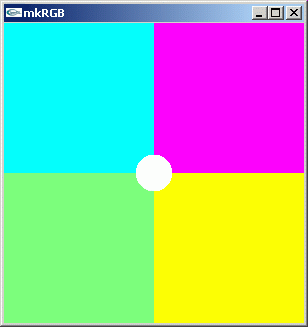
sin(z) == 0 となる z は n π (n==0,±1,±2,...) ですから、asin(0+0i) が n π の値を取る多価関数となることは理解できますが、左右のリーマン面とどのように n π の点が繋がるのか私にはイメージできません。皆様はどうでしょうか。
acos(z) と asin(z) との違いはどんなものでしょうか。
//@@ from cmath import acos from dpAnltc import * dumpFnctn(lambda z:acos(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:3.8843 Column:149 Row:0 mkRGB mtCplx -max:0.8
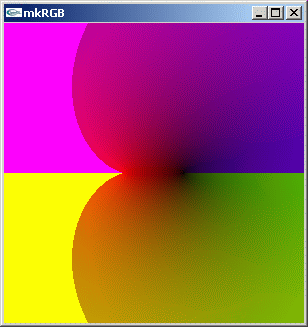

asin(z) とは異なり左右が対称ではなくなりました。その理由を探るため、-max: をデフォルトの 1 にして kkRGB 画面全部を境界領域以内に表示させます。
mkRGB mtCplx
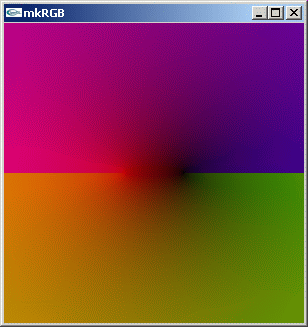

acos の左右の対称性がないのは、どうも接続の仕方によるもののように思えます。
atna(z) の複素数分布を見てみましょう。
//@@ from cmath import atan from dpAnltc import * dumpFnctn(lambda z:atan(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
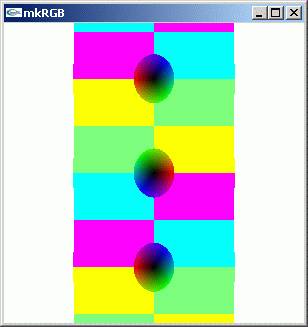
mkRGB mtCplx -max? Maximum:2.51925 Column:119 Row:149 mkRGB mtCplx -max:0.8
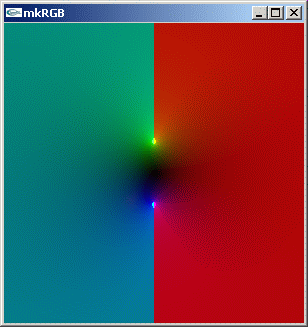
虚数軸上 i から上側に、また -i から下側にリーマン面が出ています。
ちなみに、ここの一番下に matlab を使った atan(z) のカラー位相/絶対値表示図形があります。等高線を補ってやらないと解りにくいカラー表示です。kkRGB のほうが優れていると主張します。
//@@ from scipy.special import sinh from dpAnltc import * dumpFnctn(lambda z:sinh(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:72.9835 Column:8 Row:0 mkRGB mtCplx -max:0.01

//@@ from scipy.special import cosh from dpAnltc import * dumpFnctn(lambda z:cosh(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:72.9835 Column:55 Row:0 mkRGB mtCplx -max:0.01
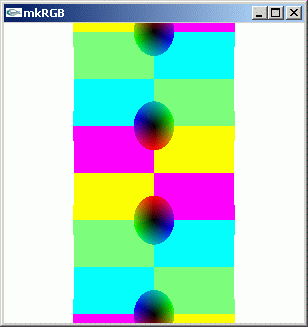

sinh(z)/cosh(z) は sin(z)/cosh(z) を π/2 だけ回転させたものであることが良く分かります。
真正特異点の周りでの位相変化/絶対値変化の様子を見てみましょう。
exp(1/z) は 0+0i を真正特異点とする解析関数です。この複素数値分布を見てみましょう。log を取っても変化が大きすぎるので、実数:[-1.0,1.0] 虚数:[1.0,-1.0] の領域に狭めます。
//@@ from scipy.special import exp from dpAnltc import * dumpLogFnctn(lambda z:exp(1/z),300,300,-1.0,1.0,1.0,-1.0) //@@@
mkRGB mtCplx -max? Maximum:1.39371e+065 Column:149 Row:150 mkRGB mtCplx -max:0.05
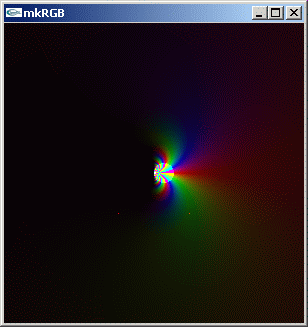

変化を解りやすくするため、スレッショルドを 1/5 だけ小さくした kkRGB 図も作っておきます。
mkRGB mtCplx -max:0.01
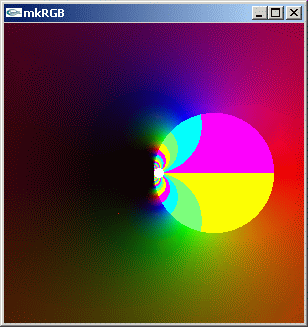

0+0i の周りで位相が急激に変化しています。でもリーマン面は存在しないようです。
//@@ from scipy.special import sin from dpAnltc import * dumpLogFnctn(lambda z:sin(1/z),300,300,-1.0,1.0,1.0,-1.0) //@@@
mkRGB mtCplx -max? Maximum:149.307 Column:149 Row:149 mkRGB mtCplx -max:0.01

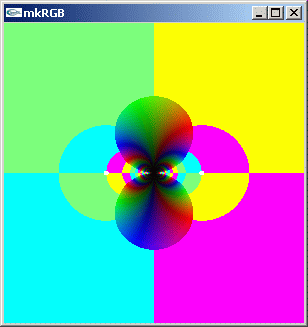
絶対値の分布が上下/左右に対称です。上下/左右に共役な関係にあることも解ります。exp(1/z) よりも対称性が明確です。
定義域を、実数:[-5.0,5.0] 虚数:[5.0,-5.0] の領域に広げてみます。
//@@ from scipy.special import sin from dpAnltc import * dumpLogFnctn(lambda z:sin(1/z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:29.3069 Column:149 Row:149 mkRGB mtCplx -max:0.01
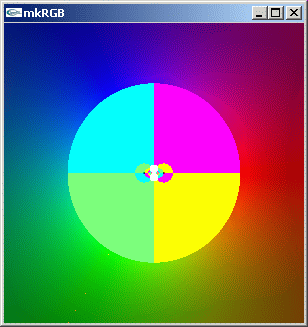
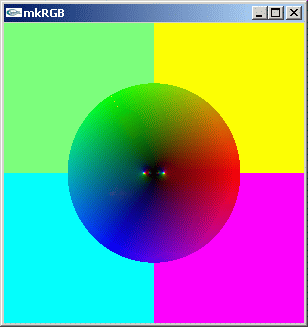
特異点は 0+0i だけのようです。右側の reversed kkkRGB 図より実数軸上に二つのゼロ点があることに気づかされます。良く見れば、前の kkRGB 図でもゼロ点が存在していました。
より狭い定義域、実数:[-0.1.0.1] 虚数:[0.1,-0.1] ではどうでしょうか。
//@@ from scipy.special import sin #from cmath import sin from dpAnltc import * dumpLogFnctn(lambda z:sin(1/z),300,300,-0.1,0.1,0.1,-0.1) //@@@
mkRGB mtCplx -max? Maximum:576.23 Column:147 Row:149 mkRGB mtCplx -max:0.01

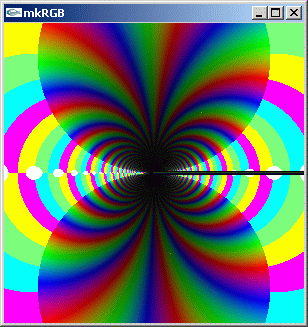
この kkRGB 図から、位相に付いてはどんなに拡大しても相似な対称性を持つようです。
ゼロ点が 0+0i の周囲に無限個ある事も分かります。先に二個のゼロ点だけが見えたのは、他のゼロ点は値域を広く取ったために表示分解能が低くかったためです。
この kkRGB 図で、正の実数軸上にある白っぽい線は計算がオーバーフローしてできた線です。log で圧縮した後で 576 の値が出てきていることから、オーバーフローが有りそうだと推測されます。
log(z) の複素数値分布を見てみましょう。
//@@ from scipy.special import log from dpAnltc import * dumpFnctn(lambda z:log(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:4.4269 Column:149 Row:149 mkRGB mtCplx
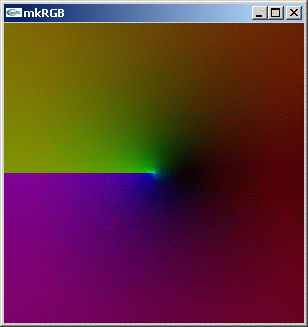
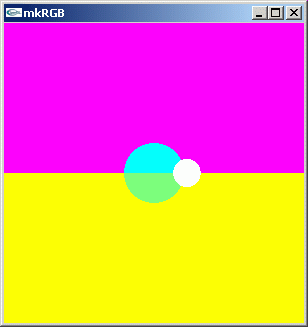
負の実数軸にリーマン面が現れています。log(z) == log(abs(z)) + i arg(z) による螺旋状の多価関数から、部分的に切り出した図になっています。純虚数値の線が -1+0i と 1+0i を通る円になっていることが良く分かります。1+0i が一次のゼロ点であることも分かります。1+0i の周りで 360度位相が回転しています。
スレッショルドを少し下げてやると等高線が現れてくるので、値と位相の変化がより分かりやすくなります。
mkRGB mtCplx -max:0.7
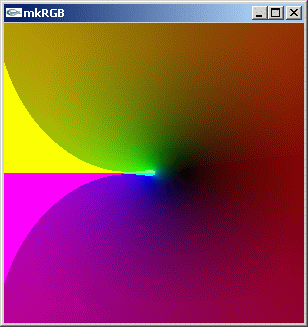

Γ(z) 関数の複素数値分布を見てみましょう。
//@@ from scipy.special import gamma from dpAnltc import * dumpLogFnctn(lambda z:gamma(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:3.78046 Column:149 Row:149 mkRGB mtCplx -max:0.5
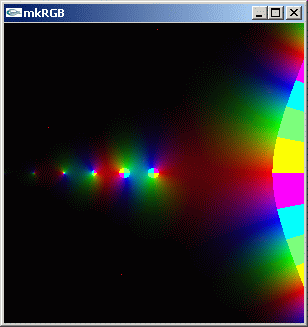

右側に行くにつれて急速に絶対値が増えることが分かります。上下に進んでいくにつれて絶対値が 0 に近づいていることも解ります。0+0i, -1+0i, -2+0i, -3+0i,... に一次の極があることが分かります。
最後に ζ(z) 関数の複素数値分布を kkRGB 図で表して見ます。ただし python の ζ(z) 関数は実数でしか定義されていません。複素数での ζ 関数が備わっていないので、ζ 関数ルーチンを作るところから始めます。
1 1 1 1
ζ(s)≡ 1 + --- + --- + --- + .... + --- + .... ------(ζ:1)式
2^s 3^s 4^s n^s
ζ(s) 関数は素数分布と関連付けられます。下のように 「1/(1-1/p^s) ただし p は素数」は次の等比級数で表せます。
1 1 1 1 1
---------- == 1 + --- + --- + --- + ---- +
1 - 1/2^s 2^1 4^s 8^s 16^s
1 1 1 1 1
---------- == 1 + --- + --- + ---- + ---- +
1 - 1/3^s 3^1 9^s 27^s 81^s
1 1 1 1 1
---------- == 1 + --- + ---- + ----- + ----- +
1 - 1/5^s 5^1 25^s 125^s 625^s
1
ζ(s) == Π --------
p∈素数 1-1/p^s
ζ(s) には素数分布など自然数の性質が凝縮しているとされ、多くの数学者がその性質を追求しています。
ζ(s) を交代級数に変形した ζ'(s) のほうが収束が早くなります。こちらの方が数値計算で値を求め易い式です。
1 1 1 1
ζ'(s)≡ 1 - --- + --- - --- + .... + --- + ....
2^s 3^s 4^s n^s
ζ(s) と ζ'(s) は下の関係があるので、収束が早い ζ'(s) を使って ζ(s) の値を求ます。
1 1 1 1
ζ'(s)≡ 1 - --- + --- - --- + .... + --- + ....
2^s 3^s 4^s n^s
1 1 1 1 1 1
ζ'(s) == ( 1 + --- + --- + --- + .... + --- + ....) - 2(+ --- + --- + .... )
2^s 3^s 4^s n^s 2^s 4^s
1 1 1 1
== ζ(s) - 2 2^(-s)(1 + --- + --- + --- + .... + --- + .... +)
2^s 3^s 4^s n^s
== (1-2 2^(-s))ζ(s)
== (1-2^(1-s))ζ(s)
ζ(s) == ζ'(s)/(1-2^(1-s)) ------- (ζ:2)式
下のように ζ`(s) を定義すると
ζ`(s) ≡ s(s-1)/2π^(-s/2)Γ(s/2)ζ(s)
ζ(s) == π^(-0.5+s) Γ((1-s)/2)/Γ(s/2) ζ(1-s) ------- (ζ:3)式
Γ(s) は 0+0i の所で発散します。それより右側の s.real が 0.5 以上の右半平面での ζ(s) 関数値を ζ'(s)/(1-2^(1-s)) から計算します。x が 0.5 より小さい左半平面での ζ(s) 値は、上の (ζ:3)式を使って、Γ(s) 関数と ζ(s) 右半平面の値より求めます。
具体的には、下の python code で複素数値まで含めた ζ(s) 値を計算します。実数部分が 0.5 以上のときは (ζ:2)式 より ζ(z) を計算します。0.5より小さい時は (ζ:2)式と(ζ:3)式を津かつて ζ(z) を計算します。
#type kZeta.py
from scipy.special import gamma, zetac, log
from scipy import *
import sfVal
def _less5zeta(s):
pi = 3.141592653589793
return pi**(-0.5+s)*gamma((1-s)/2)/gamma(s/2)*myZeta(1-s)
def myZeta(s):
_sizeN = 100
if (s.real <= 0.5):
return _less5zeta(s)
if (s.real <= 0.6):
_sizeN = 1000000
if (s.real <= 0.7):
_sizeN = 100000
if (s.real <= 0.8):
_sizeN = 20000
if (s.real <= 0.9):
_sizeN = 6000
if (s.real <= 1.0):
_sizeN = 2200
if (s.real <= 1.1):
_sizeN = 1000
if (s.real <= 1.2):
_sizeN = 550
if (s.real <= 1.3):
_sizeN = 320
if (s.real <= 1.4):
_sizeN = 140
return sum([(-1)**(x+1) * x**(-s) for x in range(1,_sizeN)])/(1-2**(1-s))
1000000, 100000, 20000, ... の数値は ζ'(s) の計算値が三桁目までの精度を持つような級数の長さを下の計算より求めて決めました。
1/1000000^0.5 < 0.001 > 1/100000^ 0.6 < 0.001 > 1/20000 ^ 0.7 < 0.000975616 > 1/6000 ^ 0.8 < 0.000949465 > 1/2200 ^ 0.9 < 0.00098134 > 1/1000 ^ 1.0 < 0.001 > 1/550 ^ 1.1 < 0.000967389 > 1/320 ^ 1.2 < 0.000985871 > 1/210 ^ 1.3 < 0.000957447 > 1/140 ^ 1.4 < 0.000989511 > 1/100 ^ 1.5 < 0.001 >
上の kZeta.py にある myZeta(z) python 関数を使って、ζ(z) の複素数値分布を kkRGB 表示させます
//@@ from kZeta import myZeta from dpAnltc import * dumpLogFnctn(lambda z:myZeta(z),300,300,-5.0,5.0,5.0,-5.0) //@@@
mkRGB mtCplx -max? Maximum:3.78508 Column:149 Row:180 mkRGB mtCplx -max:0.2
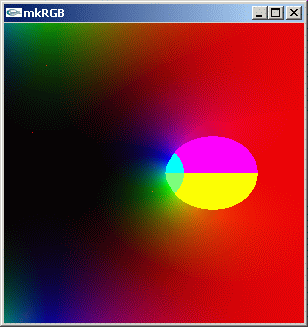
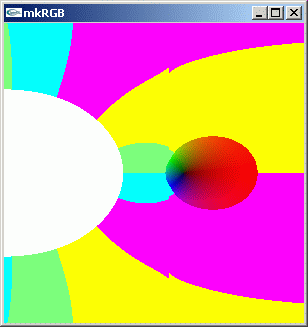
上の kkRGB 図で 0.5 + y i の直線上に小さな髭上の括れがあるのは、計算誤差の所為です。ここで反転させて計算させているため、誤差がはっきりと出てしまっています。
この kkRGB 図より、この領域では絶対値の分布は右肩上がりで、 1+0i の位置にポールが存在するのが分かります。この周辺, 実数:[0.5. 1.5] 虚数:[0.5,-0.5] の狭い領域を見てみましょう。
//@@ from kZeta import myZeta from dpAnltc import * dumpLogFnctn(lambda z:myZeta(z),300,300,0.5,1.5,0.5,-0.5) //@@@
mkRGB mtCplx -max? Maximum:6.05877 Column:149 Row:150 mkRGB mtCplx -max:0.2
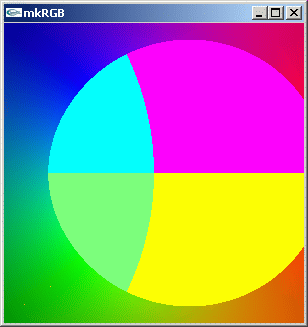
特に目だった特徴は有りません。単純な一次の極のようです。ただ、白丸が見られないので、極の立ち上がり方が狭い範囲で急峻であることが分かります。
今度は ζ(z) 関数をもっと広い領域で見てみましょう。上下に対称なのは明らかなので、実数:[-38.5. 1.5] 虚数:[38.5,-1.5] の領域とします。kkRGB 図も 500 x 500 ドットの大きな物にします
//@@ from kZeta import myZeta from dpAnltc import * dumpLogFnctn(lambda z:myZeta(z),500,500,-38.5,1.5,38.5,-1.5) //@@@
mkRGB mtCplx -max? Maximum:75.8355 Column:0 Row:0 mkRGB mtCplx -max:0.05


左上の部分で絶対値が最大となります。その位置で log 圧縮した後の値で 75.8855 の値をとります。実際の ζ(z) 関数値は結構大きな値です。
負の実数軸上 -2+0i, -4+0i, -6+0i ... に自明なゼロ点が未ら利ます。また実数軸が 1/2 の直線上のゼロ点 0.5+14.134725i, 0.5+21.022040i,0.5+25.010856 がみられます。たった六個のゼロ点しかみえませんが、規則性を感じられるゼロ点の配置幅の変化の仕方です。
ちなみに、Wolfram のここで、やはり ζ(z) 関数の複素数値分布画像を見られます。でも、実数部分と虚数部分の二つの三次元俯瞰図で表現しているため、良く分からない画像となっています。kkRGB のほうが、ずっと ζ(z) の複素数分布を直感的に掴める表示であることが良く分かります。