Two Dimensional Finite Element Method
二章「2 三角要素による形温度分布の有限要素法」と三章「3 iso-parametric 四角形要素での温度分布 有限要素法」の例題の緒言は上にあるものと同じにさせてもらいました。私の説明で分かり難いときは、こちらを見てもらうのも有効だと思います。
有限要素法に詳しくて sf がどの程度の機能を持つのか見たい方は 「2 三角要素による形温度分布の有限要素法」 を流し読みした後に「3 iso-parametric 四角形要素での温度分布 有限要素法」を読んでもらうのが手っ取り早いと思います。
議論が単純になる定常状態のみを考ます。
∂T/∂t == k △T ==0 # 温度分布は調和関数 q == -k ▽T # 熱の流れ
有限要素法要素の足し合わせによって近似温度分布 T'(x,y) があるものとします。
T'(x,y) = T0 Element0(x,y) + T1 Element1(x,y) + T2 Elemnt2(x,y) + ・・・
T'(x,y) が T(x,y) を上手く近時できているならば、△T'(x,y) の値は 0 に近くなるはずです。T'(x,y) は近似解にすぎないのですが、<T0,T1,T2,...> の値の組み合わのうち、一番上手く近似できて T*(x,y) になったとき ΔT' は最も小さくなるはずです。
R(x,y) ≡ k △T'(x,y)
と置いたとき、R(x,y) が最小になるような T*(x,y) すなわち <T*0,T*1,T*2,...> が定まったとします。そのとき T*(x,y) に微小な変分 δT 即ち <δT0,δT1,δT2,...> を与えたとき R(x,y) δT は増えるはずです。R(x,y) δT は極小値になっているはずです。
(数学に詳しい方は、「本当に R(x,y) δT は極小値になっているの? 正定値なの」と疑問に思うはずです。このことは有限要素組み合わせ関数 T'(x,y) の作り方に依存します。T'(x,y) を要素関数の足し合わせで実際に作ったときに R(x,y) δT が正定値であることが解かります。とりあえず R(x,y) δT が極小値になると仮定してください。)
以下 R(x,y) δT が極小値であることを変文法で記述してやり T'(x,y) が T*(x,y) になるための必要条件を導きます。
I(δT) ≡ ∫ R(x,y) δT(x,y) dA == o(δT) # δT よりも次数の小さい微小量
Arear
== ∫ k△T'(x,y) δT(x,y) dA
Arear
最後の式を Green の定理を使って面積分を線積分にし、微分の階数を一つ小さくして扱いやすくします。階数を下げることで、行列とベクタによる計算が可能になります。
== ∫ k▽T'(x,y)δT'(x,y) ds - ∫ k▽T'(x,y)・▽δT'(x,y) dA ------ 式(1.1)
Boundary Arear
↑ ↑
境界を出入りする 熱量 T' と δT' の熱勾配の内積の面積全体の和
上の式で、左側の項は、積分範囲の境界から出入りす熱量に δT'(x,y) の重みを掛けて境界を積分したものです。右側の項は、熱の流れ(温度勾配 x 比例乗数 k)ベクタと δT' の勾配の内積の面積分です。
T = sin(π/4 x)
Y軸 T6 T7 T8
2↑ ┌───┬───┐ │
│ │ \ ⑦│⑥ / │ │
│ │ ⑧\ │ / ⑤│ │断熱壁
0 度1│ T3├───T4───┤T5 │
│ │① / │ \ ④│ │
│ │ / ②│③ \ │ │
0│ └───┴───┘ │
T0 T1 T2
────────→ X 軸
0 1 2
0 度
図 2.1
①,②...⑧ は三角形要素で分割したときの有権要素につけた番号です
<T0,T1,T2,T3,T4,T5,T6,T7,T8> は有権要素に分割したときの接点番号 0,1,..8 の位置の温度分布です
∂T/∂t == k △T == 0 ----= 定常状態
の式がなりたちます。
T0,T1,T2, T3,T6 の位置は温度 0 で冷却されています。T2,T5,T8 は断熱壁に接触しています。
T6,T7,T8 の面に熱源が接触されていて sin (π4 x) の温度分布で暖められているとします。
この例題は此処と同じにしてあります。私の説明では端折りすぎだと感じる方は、こちらも参照願います。有限要素法の基礎から丁寧に説明されています。
まず、(0,0), (1,1),(0,1) の形状関数 N0(x,y), N1(x,y), N2(x,y) を求めます。(有限要素法に詳しくなくて形状関数の意味が判らない方は、こちらにある形状関数の説明を参照願います)下の様に N0(x,y), N1(x,y), N2(x,y) は (0,0), (1,1),(0,1) の位置より定まる行列 Form により表せます。
N0(x,y) = u0 + v0 x + w0 y, N0(x0,y0)=1, N0(x1,y1)=0, N0(x2,y2)=0
N1(x,y) = u1 + v1 x + w1 y, N1(x0,y0)=0, N1(x1,y1)=1, N1(x2,y2)=0
N2(x,y) = u2 + v2 x + w2 y, N2(x0,y0)=0, N2(x1,y1)=0, N2(x2,y2)=1
∴
│u0, v0, w0││ 1 1 1 │ = │1,0,0│
│u1, v1, w1││x0 x1 x3 │ │0,1,0│
│u2, v2, w2││y0 y1 y3 │ │0,0,1│
│u0, v0, w0│ │ 1 1 1 │^-1
│u1, v1, w1│= Form ただし Form = │x0 x1 x3 │
│u2, v2, w2│ │y0 y1 y3 │
この形状関数を使って三角要素 ① の面の上での近似温度分布を下のように表せます。
T'(x,y) == To N0(x,y) + T1 N1(x,y) + T2 N2(x,y)
== Form <T0,T1,T2> -------------------------------------------- 式(2.1)
T'(x,y) が上のように表現できれば、その温度勾配 ▽T' は下のように表現できます。とりあえず、∂T'/∂y は、下の様に表現できます。
∂T'/∂y == < <∂N0/∂y, ∂N1/∂y, ∂N2/∂y> | <T0,T1,T2> >
== < <w0, w1, w2> | <T0,T1,T2> >
== < Form[*,2] | <T0,T1,T2> >
∂T'/∂x についても同様に考え 行列 Form から、下の行列 M を作ることで ▽T を式(2.2) と、行列とベクタで表せます。
M = [[2,3]]
M[0,*] = Form[*,1]
M[1,*] = Form[*,2]
▽T' == < ∂T'/∂x, ∂T'/∂y> == M < T0, T1, T2> -------------- 式(2.2)
δT' についても同様な関係が成り立ち、また同じ M が使えます。
▽(δT') == <∂δT'/∂x, ∂δT'/∂y> == M <δT0,δT1,δT2>
図2.1 で ① の要素についての熱収支を 式 2.1 と 式 2.2 から行列計算式に変形します。
∫ k▽T'(x,y) δT'(x,y) ds - ∫ k▽T'(x,y)・ ▽δT'(x,y) dA
Boundary Arear
== -∫ qn δT'(x,y) ds - ∫ k▽T'(x,y)・ ▽δT'(x,y) dA
Boundary Arear
== -∫ qn δT'(x,y) ds - ∫ k▽T'(x,y)・ ▽δT'(x,y) dA
Boundary Arear
== -< <Q0(①),Q1(①),Q2(①)>|<δT0,δT1,δT2> > - k < M(①) <T0,T1,T2> | M(①) <δT0,δT1,δT2> > Arear(①)
↑
Node T4, T5 では 0
<Q0,Q1,Q2> は三角形の頂点から出て行く熱量です。上の関係式は ① 要素以外にも成り立ちます。全体を重ね合わせられます。
ο(δT') == - < Q0(①)+Q0(②) ,..... Q8(⑥)+Q0(⑤) | <δT0,δT1, ... ,δT8> >
- k < M(①) <T0,T1,T2> | M(①) <δT0,δT1,δT2> > Arear(①)
- k < M(②) <T0,T1,T4> | M(②) <δT0,δT1,δT4> > Arear(②)
- k < M(⑧) <T3,T4,T6> | M(⑧) <δT3,δT4,δT6> > Arear(⑧)
== - < Q0(①)+Q0(②) ,..... Q8(⑥)+Q0(⑤) | <δT0,δT1, ... ,δT8> >
- k Arear(①)< !dggr(M(①)) M(①) <T0,T1,T2> | <δT0,δT1,δT2> >
- k Arear(②)< !dggr(M(②)) M(②) <T0,T1,T4> | <δT0,δT1,δT4> >
- k Arear(⑧)< !dggr(M(⑧)) M(⑧) <T3,T4,T6> | <δT3,δT4,δT6> >
== - < Q0(①)+Q0(②) ,..... Q8(⑥)+Q0(⑤) | <δT0,δT1, ... ,δT8> > ---- 式(2.3.1)
- < Ke <T0,T1, .... T8> | <δT0,δT1, ... ,δT8> >
Ke = k Arear(①)< !dggr(M(①)) M(①) ------------------------------------- 式(2.3.2)
+ k Arear(②)< !dggr(M(②)) M(②)
・
+ k Arear(⑧)< !dggr(M(⑧)) M(⑧)
式(2.3.1) が任意の <δT0,δT1, ... ,δT8> > に対して成り立つのですから下の式が成り立ちます。
- < Q0(①)+Q0(②) ,..... Q8(⑥)+Q0(⑤)> == Ke <T0,T1, .... T8> --------------- 式 (2.3.3)
全体を足し合わせたとき、左側のの項が境界から出入りする熱量になります。<Q0, Q1, Q2, Q3, .... Q8> と各ノードから出て行く熱量とできます。
図 2.1, 式(2.3.3) の剛性行列 Ke を具体的に sf を使って計算します。式(2.3.2) の計算を実際に行います。
//@@
@@subFile Form
_rt = [[3]]
_rt[0,*]=<1, 1, 1>
_rt[1,*]=<Node{p}[0], Node{q}[0], Node{r}[0]>
_rt[2,*]=<Node{p}[1], Node{q}[1], Node{r}[1]>
_rt = _rt^(-1)
@@endSubFile
@@subFile SetKatKe
_rt=0
Ke[p,p] = Ke[p,p]+B[0,0], Ke[p,q] = Ke[p,q]+B[0,1], Ke[p,r] = Ke[p,r]+B[0,2]
Ke[q,p] = Ke[q,p]+B[1,0], Ke[q,q] = Ke[q,q]+B[1,1], Ke[q,r] = Ke[q,r]+B[1,2]
Ke[r,p] = Ke[r,p]+B[2,0], Ke[r,q] = Ke[r,q]+B[2,1], Ke[r,r] = Ke[r,r]+B[2,2]
@@endSubFile
@@subFile MakeB
_rt=0
M[0,*] = (@Form())[*,1] # x poisition
M[1,*] = (@Form())[*,2] # y poisition
B = k !dggr(M) M Area
@@endSubFile
k@
Kt@
#B@
M@
x0@,x1@,x2@, y0@,y1@, y2@, N@, Area@
# triangular node index
p@,q@,r@
# Node data
Node{0}@=<0,0>,Node{1}@=<0,1>,Node{2}@=<0,2>
Node{3}@=<1,0>,Node{4}@=<1,1>,Node{5}@=<1,2>
Node{6}@=<2,0>,Node{7}@=<2,1>,Node{8}@=<2,2>
N=9
Ke = [[N]]
Area = 0.5
k=1
M = [[2,3]]
#①: 0,4,3 節点 <0,0>, <1,1>, <0,1> についての local stiffness matrix B を求める
# counter clockwise に 0,4,3 節点 を選択します
p =0, q=4, r=3
@MakeB()
@SetKatKe()
#②: 0,1,4 節点
p =0, q=1, r=4
@MakeB()
@SetKatKe()
#③: 1,2,4 節点
p =1, q=2, r=4
@MakeB()
@SetKatKe()
#④: 2,5,4 節点
p =2, q=5, r=4
@MakeB()
@SetKatKe()
#⑤: 5,8,4 節点
p =5, q=8, r=4
@MakeB()
@SetKatKe()
#⑥: 8,7,4 節点
p =8, q=7, r=4
@MakeB()
@SetKatKe()
#⑦: 7,6,4 節点
p =7, q=6, r=4
@MakeB()
@SetKatKe()
#⑧: 6,3,4 節点
p =6, q=3, r=4
@MakeB()
@SetKatKe()
//@@@
# 剛性行列 Ke の計算結果
< 1, -0.5, 0, -0.5, 0, 0, 0, 0, 0 >
< -0.5, 2, -0.5, 0, -1, 0, 0, 0, 0 >
< 0, -0.5, 1, 0, 0, -0.5, 0, 0, 0 >
< -0.5, 0, 0, 2, -1, 0, -0.5, 0, 0 >
< 0, -1, 0, -1, 4, -1, 0, -1, 0 >
< 0, 0, -0.5, 0, -1, 2, 0, 0, -0.5 >
< 0, 0, 0, -0.5, 0, 0, 1, -0.5, 0 >
< 0, 0, 0, 0, -1, 0, -0.5, 2, -0.5 >
< 0, 0, 0, 0, 0, -0.5, 0, -0.5, 1 >
Jacobi.exe Ke.val
< 4.92678e-016, 0.633975, 0.633975, 1, 1.69722, 2, 2.36603, 2.36603, 5.30278 >
歪と応力の剛性行列のときとは異なり、固有値は一つだけが 0 になります。熱方程式は、温度のオフセット分一つだけ自由度であることに対応します。
境界条件を設定して温度分布を求めます。
図 2.1 の境界条件は下の sf 式で表されます。
<T0,T1,T2> = <0,0,0> #0 度、
<T6,T7,T8> = < sin(π/4 0), sin(π/4 1), sin(π/4 2)>
まず、上で得られた剛性行列 Ke のうち、温度が固定されているノードの行を単位行列に直した剛性行列 K を作ります。
//@@
K=Ke
e1 = <1,0,0,0, 0,0,0,0, 0>
K[0,*]=e1
K[1,*]=~shift(e1,1)
K[2,*]=~shift(e1,2)
K[3,*]=~shift(e1,3)
K[6,*]=~shift(e1,6)
K[7,*]=~shift(e1,7)
K[8,*]=~shift(e1,8)
//@@@
熱源の境界条件を fixed ベクタで与えます。
fixed = <0,0,0,0, 0,0,0,!sin(π/4 1), !sin(π/4 2)>
distribution ベクタはは温度固定点( 境界条件)による、非固定点ノードの熱の流れの寄与分を表します。
distribution = fixed - K fixed # fixed が境界条件です
< 0, 0, 0, 0, 0.707107, 0.5, 0, 0, 0 >
K を、剛性行列から境界条件ノードを取り去ったものにします。
//@@
K[*,1]=~shift(e1,1)
K[*,2]=~shift(e1,2)
K[*,3]=~shift(e1,3)
K[*,6]=~shift(e1,6)
K[*,7]=~shift(e1,7)
K[*,8]=~shift(e1,8)
//@@@
< 1, 0, 0, 0, 0, 0, 0, 0, 0 >
< 0, 1, 0, 0, 0, 0, 0, 0, 0 >
< 0, 0, 1, 0, 0, 0, 0, 0, 0 >
< 0, 0, 0, 1, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, 4, -1, 0, 0, 0 >
< 0, 0, 0, 0, -1, 2, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0, 1, 0, 0 >
< 0, 0, 0, 0, 0, 0, 0, 1, 0 >
< 0, 0, 0, 0, 0, 0, 0, 0, 1 >
4,5 ノードの熱流が差し引き 0 になっているので、T4,T5 の温度が下の計算で求められます。
K^-1 distribution
< 0, 0, 0, 0, 0.273459, 0.38673, 0, 0, 0 >
ノード全体の温度分布は下のように計算できます。
Tdstrbtn = K^-1 distribution + fixed
< 0, 0, 0, 0, 0.273459, 0.38673, 0, 0.707107, 1 >
熱量の流れは下のように計算できます
Ke Tdstrbtn
< 0, -0.273459, -0.193365, -0.273459, 2.22045e-016, -5.55112e-017, -0.353553, 0.640754, 0.453082 >
< T0, T1, T2, T3, T4, T5, T6, T7, T8 >
以上の計算によって、式(1,1) の値を最小にする 図 2.1 の九つの節点の温度分布 <T0,T1,T2,T3,T4,T5,T6,T7,T8 > を計算できました。
T = sin(π/4 x)
Y T6 T7 T8
2↑ ┌───┬───┐ │
│ │ ② │ ④ │ │
│ │ │ │ │断熱壁
0 度1│ T3├───T4───┤T5 │
│ │ │ │ │
│ │ ① │ ③ │ │
0│ └───┴───┘ │
T0 T1 T2
────────→ X
0 1 2
0 度
図 3.1
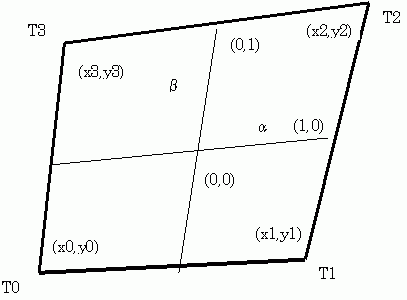
四角形要素 ① の内部の点の座標 (x,y) は下の式で表せます。
x = 1/4((1-α)(1-β)x0 + (1+α)(1-β)x1 + (1+α)(1+β)x2 + (1-α)(1+β)x3) # α、β∈[-1,1)
y = 1/4((1-α)(1-β)y0 + (1+α)(1-β)y1 + (1+α)(1+β)y2 + (1-α)(1+β)y3)
四角形要素 ① の内部の近似温度分布 T'(x,y) は下の式で表せます。
T'= 1/4((1-α)(1-β)T0 + (1+α)(1-β)T1 + (1+α)(1+β)T2 + (1-α)(1+β)T3) # α、β∈[-1,1)
(<T0,T1,T2,T3> は図3.1 の <T0,T1,T4,T3> に対応します)
Jacobian 行列 Jは、下の式で表せます。
∂(x, y )
----------- = J: Jacobian 行列
∂(α, β)
J== │ 1/4( -(1-β)x0 + (1-β)x1 + (1+β)x2 - (1+β)x3), 1/4( -(1-β)y0 + (1-β)y1 + (1+β)y2 - (1+β)y3) │
│ 1/4( -(1-α)x0 - (1-α)x1 + (1+α)x2 + (1+α)x3), 1/4( -(1-α)y0 - (1-α)y1 + (1+α)y2 + (1+α)y3) │
▽T は下の式で表せもます
<∂T'/∂α, ∂T'/∂β> == J <∂T'/∂x, ∂T'/∂y>
<∂T'/∂α, ∂T'/∂β> == |-(1-β)/4, (1-β)/4, (1+β)/4, -(1+β)/4 |*<T0, T1, T2, T3>
|-(1-α)/4, -(1+α)/4, (1+α)/4, (1-α)/4 |
== B <T0, T1, T2, T3> ------------------------------- 式(3,1)
ただし
B == |-(1-β)/4, (1-β)/4, (1+β)/4, -(1+β)/4 |
|-(1-α)/4, -(1+α)/4, (1+α)/4, (1-α)/4 |
<∂δT'/∂α, ∂δT'/∂β> == B <δT0, δT1, δT2, δT3>
▽T' == <∂T'/∂x, ∂T'/∂y> == J^-1 <∂T'/∂α, ∂T'/∂β> -------- 式(3,2)
▽δT' == <∂δT'/∂x, ∂δT'/∂y> == J^-1 <∂δT'/∂α, ∂δT'/∂β>
①の要素についての熱収支を 式(1.1)と 式(3.1) 式(3.2) から行列ベクタ式にします。
∫ k▽T'(x,y) δT'(x,y) ds - ∫ k▽T'(x,y)・ ▽δT'(x,y) dA
Boundary Arear
== -∫ qn δT'(x,y) ds - ∫ k▽T'(x,y)・ ▽δT'(x,y) dA
Boundary Arear
== -∫ qn δT'(x,y) ds - ∫ k▽T'(x,y)・ ▽δT'(x,y) !det(J) dαdβ
Boundary α∈[-1,1), β∈[-1,1)
== ∫ qn δT'(x,y) ds - k∫ < J^-1 B <T0, T1, T2, T3> | ▽δT(x,y) > !det(J) dα dβ
Boundary α∈[-1,1), β∈[-1,1)
== k < <δT0,δT1,δT2,δT3>|<Q0,Q1,Q2,Q3> > #Node 0,1,2,3 からで流れる熱量
- k ∫<B<δT0,δT1,δT2,δT3>|J^-1 B <T0, T1, T2, T3> > !det(J)| dαdβ #温度分布
α∈[-1,1), β∈[-1,1)
== k < <δT0,δT1,δT2,δT3>|<Q0,Q1,Q2,Q3> > ------------------------------ 式(3.3)
- k < <δT0,δT1,δT2,δT3> |∫!dggr(J^-1 B) J^-1 B !det(J)| dαdβ| <T0, T1, T2, T3> >
α∈[-1,1), β∈[-1,1)
三角要素のときと同様に、式(3.3) を T0,T1, ... T8 全部について足し合わせて剛性行列 ke を作ります。 3.3 式が任意の <δT0,δT1, ... ,δT8> に対して成り立つのですから、やはり下の式が成り立ちます。
- < Q0, Q1, ,..... ,Q8> == Ke <T0,T1, .... T8> -------------- 式(3.4)
ただし α∈[-1,1), β∈[-1,1) の範囲の積分は、ガウスの積分公式を使って積分を足し算に簡略化します。
//@@
col=2, row = 2
Node = [[(col+1)(row+1),2]]
Node[<0,9*2,1>]=\
< 0,0
1,0
2,0
0,1
1,1
2,1
0,2
1,2
2,2>
Mesh = [[col*row,4]]
Mesh[<0,4*4,1>]=\
< 0,1,4,3
3,4,7,6
1,2,5,4
4,5,8,7>
//@@@
//@@
@@subFile J
_rt =[[2]]
_rt[0,*] = <(-(1-β)x0 + (1-β)x1 + (1+β)x2 - (1+β)x3)/4
, (-(1-β)y0 + (1-β)y1 + (1+β)y2 - (1+β)y3)/4>
_rt[1,*] = <(-(1-α)x0 - (1+α)x1 + (1+α)x2 + (1-α)x3)/4
, (-(1-α)y0 - (1+α)y1 + (1+α)y2 + (1-α)y3)/4>
@@endSubFile
@@subFile B
_rt = [[2,4]]
_rt[0,*]= <-(1-β)/4, (1-β)/4, (1+β)/4, -(1+β)/4>
_rt[1,*]= <-(1-α)/4, -(1+α)/4, (1+α)/4, (1-α)/4>
@@endSubFile
@@subFile makeK #(α,β) 引数
α@= _prm1
β@= _prm2
_rt = !dggr(@B())!dggr(@J()^-1) @J()^-1 @B() !det(@J())
@@endSubFile
@@subFile SetKatKe
Ke[p,p] = Ke[p,p] + K[0,0]
Ke[p,q] = Ke[p,q] + K[0,1]
Ke[p,r] = Ke[p,r] + K[0,2]
Ke[p,s] = Ke[p,s] + K[0,3]
Ke[q,p] = Ke[q,p] + K[1,0]
Ke[q,q] = Ke[q,q] + K[1,1]
Ke[q,r] = Ke[q,r] + K[1,2]
Ke[q,s] = Ke[q,s] + K[1,3]
Ke[r,p] = Ke[r,p] + K[2,0]
Ke[r,q] = Ke[r,q] + K[2,1]
Ke[r,r] = Ke[r,r] + K[2,2]
Ke[r,s] = Ke[r,s] + K[2,3]
Ke[s,p] = Ke[s,p] + K[3,0]
Ke[s,q] = Ke[s,q] + K[3,1]
Ke[s,r] = Ke[s,r] + K[3,2]
Ke[s,s] = Ke[s,s] + K[3,3]
_rt=0
@@endSubFile
//@@@
//@@
x0@,x1@,x2@,x3@, y0@,y1@,y2@,y3@,N@
N = (col+1)*(row+1)
Ke @= [[ N ]]
j@=0
x0=Node[Mesh[j,0],0], y0=Node[Mesh[j,0],1],x1=Node[Mesh[j,1],0], y1=Node[Mesh[j,1],1]
x2=Node[Mesh[j,2],0], y2=Node[Mesh[j,2],1],x3=Node[Mesh[j,3],0], y3=Node[Mesh[j,3],1]
K = @makeK(-0.57735, -0.57735) + @makeK(+0.57735, -0.57735) + @makeK(-0.57735, +0.57735) + @makeK(+0.57735, +0.57735)
p=Mesh[j,0],q=Mesh[j,1],r=Mesh[j,2],s=Mesh[j,3]
@SetKatKe()
j=1
x0=Node[Mesh[j,0],0], y0=Node[Mesh[j,0],1],x1=Node[Mesh[j,1],0], y1=Node[Mesh[j,1],1]
x2=Node[Mesh[j,2],0], y2=Node[Mesh[j,2],1],x3=Node[Mesh[j,3],0], y3=Node[Mesh[j,3],1]
K = @makeK(-0.57735, -0.57735) + @makeK(+0.57735, -0.57735) + @makeK(-0.57735, +0.57735) + @makeK(+0.57735, +0.57735)
p=Mesh[j,0],q=Mesh[j,1],r=Mesh[j,2],s=Mesh[j,3]
@SetKatKe()
j=2
x0=Node[Mesh[j,0],0], y0=Node[Mesh[j,0],1],x1=Node[Mesh[j,1],0], y1=Node[Mesh[j,1],1]
x2=Node[Mesh[j,2],0], y2=Node[Mesh[j,2],1],x3=Node[Mesh[j,3],0], y3=Node[Mesh[j,3],1]
K = @makeK(-0.57735, -0.57735) + @makeK(+0.57735, -0.57735) + @makeK(-0.57735, +0.57735) + @makeK(+0.57735, +0.57735)
p=Mesh[j,0],q=Mesh[j,1],r=Mesh[j,2],s=Mesh[j,3]
@SetKatKe()
j=3
x0=Node[Mesh[j,0],0], y0=Node[Mesh[j,0],1],x1=Node[Mesh[j,1],0], y1=Node[Mesh[j,1],1]
x2=Node[Mesh[j,2],0], y2=Node[Mesh[j,2],1],x3=Node[Mesh[j,3],0], y3=Node[Mesh[j,3],1]
K = @makeK(-0.57735, -0.57735) + @makeK(+0.57735, -0.57735) + @makeK(-0.57735, +0.57735) + @makeK(+0.57735, +0.57735)
p=Mesh[j,0],q=Mesh[j,1],r=Mesh[j,2],s=Mesh[j,3]
@SetKatKe()
Ke{col*row} = Ke
//@@@
sf Ke{4}
< 0.666667, -0.166667, 0, -0.166667, -0.333333, 0, 0, 0, 0 >
< -0.166667, 1.33333, -0.166667, -0.333333, -0.333333, -0.333333, 0, 0, 0 >
< 0, -0.166667, 0.666667, 0, -0.333333, -0.166667, 0, 0, 0 >
< -0.166667, -0.333333, 0, 1.33333, -0.333333, 0, -0.166667, -0.333333, 0 >
< -0.333333, -0.333333, -0.333333, -0.333333, 2.66667, -0.333333, -0.333333, -0.333333, -0.333333 >
< 0, -0.333333, -0.166667, 0, -0.333333, 1.33333, 0, -0.333333, -0.166667 >
< 0, 0, 0, -0.166667, -0.333333, 0, 0.666667, -0.166667, 0 >
< 0, 0, 0, -0.333333, -0.333333, -0.333333, -0.166667, 1.33333, -0.166667 >
< 0, 0, 0, 0, -0.333333, -0.166667, 0, -0.166667, 0.666667 >
# 確認計算
Jacobi.exe Ke{4}
< -3.18348e-016, 0.591752, 0.591752, 0.666667, 1, 1.40825, 1.40825, 2, 3 >
まず、上で得られた剛性行列のうち、温度が固定されているようノードの行を単位行列に直します。
//@@
K=Ke{4}
e1 = <1,0,0,0, 0,0,0,0, 0>
K[0,*]=e1
K[1,*]=~shift(e1,1)
K[2,*]=~shift(e1,2)
K[3,*]=~shift(e1,3)
K[6,*]=~shift(e1,6)
K[7,*]=~shift(e1,7)
K[8,*]=~shift(e1,8)
//@@@
三角要素のときと同様に、図 3.1 の境界条件を下のように設定します。
fixed = <0,0,0,0, 0,0,0,!sin(π/4 1), !sin(π/4 2)>
distribution は温度固定点( 境界条件)による、非固定点ノードの熱の流れの寄与分です。
distribution = fixed - K fixed # fixed は境界条件です
< 0, 0, 0, 0, 0.569036, 0.402369, 0, 0, 0 >
K を、剛性行列から境界条件ノードを取り去ったものにします。
//@@
K[*,0]=~shift(e1,0)
K[*,1]=~shift(e1,1)
K[*,2]=~shift(e1,2)
K[*,3]=~shift(e1,3)
K[*,6]=~shift(e1,6)
K[*,7]=~shift(e1,7)
K[*,8]=~shift(e1,8)
//@@@
< 1, 0, 0, 0, 0, 0, 0, 0, 0 >
< 0, 1, 0, 0, 0, 0, 0, 0, 0 >
< 0, 0, 1, 0, 0, 0, 0, 0, 0 >
< 0, 0, 0, 1, 0, 0, 0, 0, 0 >
< 0, 0, 0, 0, 2.66667, -0.333333, 0, 0, 0 >
< 0, 0, 0, 0, -0.333333, 1.33333, 0, 0, 0 >
< 0, 0, 0, 0, 0, 0, 1, 0, 0 >
< 0, 0, 0, 0, 0, 0, 0, 1, 0 >
< 0, 0, 0, 0, 0, 0, 0, 0, 1 >
4,5 ノードの熱流が差し引き 0 になるようはずであり、T4,T5 の温度が下の計算で求められます。
K^-1 distribution
< 0, 0, 0, 0, 0.259211, 0.366579, 0, 0, 0 >
参考:三角要素のときの値
< 0, 0, 0, 0, 0.273459, 0.38673, 0, 0, 0 >
当然ながら、三角要素のときの計算と似た値になるます。
ノード全体の温度分布は下のように計算できます
Tdstrbtn = K^-1 distribution + fixed
< 0, 0, 0, 0, 0.259211, 0.366579, 0, 0.707107, 1 >
熱量の流れは下のように計算できます
Ke{4} Tdstrbtn
< -0.0864036, -0.208597, -0.1475, -0.322106, 1.11022e-016, -2.77556e-017, -0.204255, 0.567546, 0.401315 >
下のようなパラメトリック要素による 6x10 分割された 2cm の正方形板の定常温度分布を計算します。メッシュ分割以外は図 3.1 のときと同じです。ただし、この数値例は、他の Web ページにありません。
T=0 温度分布:sin(π/4 x) 位置 断熱壁
┃|6 13 20 27 34 41 48 55 62 69 76 ┃
┃|------+------+------+------+------+------+------+------+------+------+2*6/6 ┃
┃| M:5 | M:11 | M:17 | M:23 | M:29 | M:35 | M:41 | M:47 | M:53 | M:59 | ┃
┃|5 12| 19| 26| 33| 40| 47| 54| 61| 68| 75| ┃
┃|------+------+------+------+------+------+------+------+------+------+2*5/6 ┃
┃| M:4 | M:10 | M:16 | M:22 | M:28 | M:34 | M:40 | M:46 | M:52 | M:58 | ┃
┃|4 11| 18| 25| 32| 39| 46| 53| 60| 67| 74| ┃
┃|------+------+------+------+------+------+------+------+------+------+2*4/6 ┃
┃| M:3 | M:9 | M:15 | M:21 | M:27 | M:33 | M:39 | M:45 | M:51 | M:57 | ┃
┃|3 10| 17| 24| 31| 38| 45| 52| 59| 66| 73| ┃
┃|------+------+------+------+------+------+------+------+------+------+2*3/6 ┃
┃| M:2 | M:8 | M:14 | M:20 | M:26 | M:31 | M:38 | M:44 | M:50 | M:55 | ┃
┃|2 9| 16| 23| 30| 37| 44| 51| 58| 65| 72| ┃
┃|------+------+------+------+------+------+------+------+------+------+2*2/6 ┃
┃| M:1 | M:7 | M:13 | M:19 | M:25 | M:31 | M:37 | M:43 | M:49e| M:55 | ┃
┃|1 8| 15| 22| 29| 36| 43| 50| 57| 64| 71| ┃
┃|------+------+------+------+------+------+------+------+------+------+2*1/6 ┃
┃| M:0 | M:6 | M:12 | M:18 | M:24 | M:30 | M:36 | M:42 | M:48 | M:54 | ┃
┃|0 7| 14| 21| 28| 35| 42| 49| 56| 63| 70| ┃
┃|------+------+------+------+------+------+------+------+------+------+ ┃
┃|0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0:位置
┗━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━T=0
図 4.1
//@@
col=6, row = 10
Node = [[(col+1)(row+1),2]]
Node[<0,(col+1)(row+1)*2,1>]=\
< 0.0 ,0, 0.0 ,2*1/6, 0.0 ,2*2/6, 0.0 ,2*3/6, 0.0 ,2*4/6, 0.0 ,2*5/6, 0.0 ,2*6/6
0.2 ,0, 0.2 ,2*1/6, 0.2 ,2*2/6, 0.2 ,2*3/6, 0.2 ,2*4/6, 0.2 ,2*5/6, 0.2 ,2*6/6
0.4 ,0, 0.4 ,2*1/6, 0.4 ,2*2/6, 0.4 ,2*3/6, 0.4 ,2*4/6, 0.4 ,2*5/6, 0.4 ,2*6/6
0.6 ,0, 0.6 ,2*1/6, 0.6 ,2*2/6, 0.6 ,2*3/6, 0.6 ,2*4/6, 0.6 ,2*5/6, 0.6 ,2*6/6
0.8 ,0, 0.8 ,2*1/6, 0.8 ,2*2/6, 0.8 ,2*3/6, 0.8 ,2*4/6, 0.8 ,2*5/6, 0.8 ,2*6/6
1.0 ,0, 1.0 ,2*1/6, 1.0 ,2*2/6, 1.0 ,2*3/6, 1.0 ,2*4/6, 1.0 ,2*5/6, 1.0 ,2*6/6
1.2 ,0, 1.2 ,2*1/6, 1.2 ,2*2/6, 1.2 ,2*3/6, 1.2 ,2*4/6, 1.2 ,2*5/6, 1.2 ,2*6/6
1.4 ,0, 1.4 ,2*1/6, 1.4 ,2*2/6, 1.4 ,2*3/6, 1.4 ,2*4/6, 1.4 ,2*5/6, 1.4 ,2*6/6
1.6 ,0, 1.6 ,2*1/6, 1.6 ,2*2/6, 1.6 ,2*3/6, 1.6 ,2*4/6, 1.6 ,2*5/6, 1.6 ,2*6/6
1.8 ,0, 1.8 ,2*1/6, 1.8 ,2*2/6, 1.8 ,2*3/6, 1.8 ,2*4/6, 1.8 ,2*5/6, 1.8 ,2*6/6
2.0 ,0, 2.0 ,2*1/6, 2.0 ,2*2/6, 2.0 ,2*3/6, 2.0 ,2*4/6, 2.0 ,2*5/6, 2.0 ,2*6/6>
Mesh = [[col*row,4]]
Mesh[<0,col*row*4,1>]=\
< 0,7,8,10, 1,8,9,23, 2,9,10,3, 3,10,11,4, 4,11,12,5, 5,12,13,6,
7,14,15,8, 8,15,16,9, 9,16,17,10, 10,17,18,11, 11,18,19,12, 12,19,20,13,
14,21,22,15, 15,22,23,16, 16,23,24,17, 17,24,25,18, 18,25,26,19, 19,26,27,20,
21,28,29,22, 22,29,30,23, 23,30,31,24, 24,31,32,25, 25,32,33,26, 26,33,34,27,
28,35,36,29, 29,36,37,30, 30,37,38,31, 31,38,39,32, 32,39,40,33, 33,40,41,34,
35,42,43,36, 36,43,44,37, 37,44,45,38, 38,45,46,39, 39,46,47,40, 40,47,48,41,
42,49,50,43, 43,50,51,44, 44,51,52,45, 45,52,53,46, 46,53,54,47, 47,54,55,48,
49,56,57,50, 50,57,58,51, 51,58,59,52, 52,59,60,53, 53,60,61,54, 54,61,62,55,
56,63,64,57, 57,64,65,58, 58,65,66,59, 59,66,67,60, 60,67,68,61, 61,68,69,62,
63,70,71,64, 64,71,72,65, 65,72,73,66, 66,73,74,67, 67,74,75,68, 68,75,76,69>
//@@@
//@@
x0@,x1@,x2@,x3@, y0@,y1@,y2@,y3@,N@
N = (col+1)*(row+1)
Ke @= [[ N ]] # to spped up calculation
<<0,col*row,1@j|\
x0=Node[Mesh[j,0],0], y0=Node[Mesh[j,0],1],x1=Node[Mesh[j,1],0], y1=Node[Mesh[j,1],1]
x2=Node[Mesh[j,2],0], y2=Node[Mesh[j,2],1],x3=Node[Mesh[j,3],0], y3=Node[Mesh[j,3],1]
K = @makeK(-0.57735, -0.57735) + @makeK(+0.57735, -0.57735) + @makeK(-0.57735, +0.57735) + @makeK(+0.57735, +0.57735)
p=Mesh[j,0],q=Mesh[j,1],r=Mesh[j,2],s=Mesh[j,3]
@SetKatKe()
>>
Ke{col*row} = Ke
//@@@
Jacobi.exe Ke{60}.val
< -2.4915e-016, 0.0698, 0.111646, 0.140133, 0.217109, 0.386407, 0.421698,
0.42863, 0.579017, 0.684991, 0.727734, 0.744199, 0.812786, 0.950463,
0.96885, 1.0232, 1.09159, 1.09548, 1.18794, 1.21233, 1.22829,
1.29079, 1.34038, 1.41636, 1.44489, 1.45943, 1.54873, 1.61572,
1.64489, 1.74924, 1.77082, 1.80915, 1.865, 1.90007, 1.95859,
1.97646, 1.99931, 2.00109, 2.04947, 2.05961, 2.06859, 2.13434,
2.2279, 2.31131, 2.35847, 2.38985, 2.50277, 2.63194, 2.67723,
2.74026, 2.79537, 2.82209, 2.91233, 2.99947, 3.11144, 3.18348,
3.24667, 3.3126, 3.3334, 3.44174, 3.5933, 3.66268, 3.82574,
3.93174, 4.0372, 4.08721, 4.31806, 4.56669, 4.69513, 4.84271,
4.95838, 5.30292, 5.42485, 5.75665, 5.92887, 6.32018, 12.1265 >
//@@
KTemp@=Ke{60}
e1 = <<(col+1)(row+1)>>
e1[0]=1
KTemp[0,*]=e1
KTemp[1,*]=~shift(e1,1)
KTemp[2,*]=~shift(e1,2)
KTemp[3,*]=~shift(e1,3)
KTemp[4,*]=~shift(e1,4)
KTemp[5,*]=~shift(e1,5)
KTemp[6,*]=~shift(e1,6)
KTemp[7,*]=~shift(e1,7)
KTemp[14,*]=~shift(e1,14)
KTemp[21,*]=~shift(e1,21)
KTemp[28,*]=~shift(e1,28)
KTemp[35,*]=~shift(e1,35)
KTemp[42,*]=~shift(e1,42)
KTemp[49,*]=~shift(e1,49)
KTemp[56,*]=~shift(e1,56)
KTemp[63,*]=~shift(e1,63)
KTemp[70,*]=~shift(e1,70)
KTemp[13,*]=~shift(e1,13)
KTemp[20,*]=~shift(e1,20)
KTemp[27,*]=~shift(e1,27)
KTemp[34,*]=~shift(e1,34)
KTemp[41,*]=~shift(e1,41)
KTemp[48,*]=~shift(e1,48)
KTemp[55,*]=~shift(e1,55)
KTemp[62,*]=~shift(e1,62)
KTemp[69,*]=~shift(e1,69)
KTemp[76,*]=~shift(e1,76)
K=KTemp
//@@@
例題 3.1 のときと同様に考えて、図 4.1 の境界条件を下のように設定します。
fixed = <<(col+1)(row+1)>>
fixed[<6,row+1,7>] = <<0,row+1,1@j|!sin(π/4 2(j/row) )>>
distribution (温度固定点 による、非固定点ノードの熱の流れの寄与分) を計算します。
distribution = fixed - K fixed # fixed が境界条件であり、 distribution は fixed に重ね合わせる温度分布
< 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0.0924055, 0, 0, 0, 0, 0,
0, 0.182536, 0, 0, 0, 0, 0, 0, 0.268171,
0, 0, 0, 0, 0, 0, 0.347203, 0, 0,
0, 0, 0, 0, 0.417686, 0, 0, 0, 0,
0, 0, 0.477885, 0, 0, 0, 0, 0, 0,
0.526316, 0, 0, 0, 0, 0, 0, 0.561787, 0,
0, 0, 0, 0, 0, 0.583425, 0, 0, 0,
0, 0, 0, 0.295349, 0 >
K を、剛性行列から境界条件ノードを取り去ったものにします。
//@@
KTemp@=K
KTemp[*,1]=~shift(e1,1)
KTemp[*,2]=~shift(e1,2)
KTemp[*,3]=~shift(e1,3)
KTemp[*,4]=~shift(e1,4)
KTemp[*,5]=~shift(e1,5)
KTemp[*,6]=~shift(e1,6)
KTemp[*, 7]=~shift(e1,7)
KTemp[*,14]=~shift(e1,14)
KTemp[*,21]=~shift(e1,21)
KTemp[*,28]=~shift(e1,28)
KTemp[*,35]=~shift(e1,35)
KTemp[*,42]=~shift(e1,42)
KTemp[*,49]=~shift(e1,49)
KTemp[*,56]=~shift(e1,56)
KTemp[*,63]=~shift(e1,63)
KTemp[*,70]=~shift(e1,70)
KTemp[*,13]=~shift(e1,13)
KTemp[*,20]=~shift(e1,20)
KTemp[*,27]=~shift(e1,27)
KTemp[*,34]=~shift(e1,34)
KTemp[*,41]=~shift(e1,41)
KTemp[*,48]=~shift(e1,48)
KTemp[*,55]=~shift(e1,55)
KTemp[*,62]=~shift(e1,62)
KTemp[*,69]=~shift(e1,69)
KTemp[*,76]=~shift(e1,76)
K=KTemp
//@@@
温度分布を計算します
Tdstrbtn = K^-1 distribution + fixed
< -5.72533e-017, 0, 0, 0, 0, 0, 0,
0, 0.0263525, 0.0479307, 0.0624282, 0.0859634, 0.116998, 0.156434,
0, 0.0417259, 0.0823771, 0.121672, 0.169527, 0.231056, 0.309017,
0, 0.0564347, 0.120133, 0.175752, 0.248643, 0.339292, 0.45399,
0, 0.0712809, 0.146021, 0.226142, 0.321092, 0.439088, 0.587785,
0, 0.0837949, 0.172039, 0.270005, 0.385599, 0.527962, 0.707107,
0, 0.0946571, 0.194974, 0.307517, 0.440513, 0.603811, 0.809017,
0, 0.103545, 0.213681, 0.337784, 0.48464, 0.664793, 0.891007,
0, 0.110128, 0.227482, 0.360002, 0.51695, 0.709441, 0.951057,
0, 0.114168, 0.235935, 0.373574, 0.53666, 0.736671, 0.987688,
0, 0.11553, 0.238781, 0.378138, 0.543285, 0.745823, 1 >
実務での計差では、この程度の精度の計算でも十分なところも多いと思います。 sf の活用を検討してみてください。
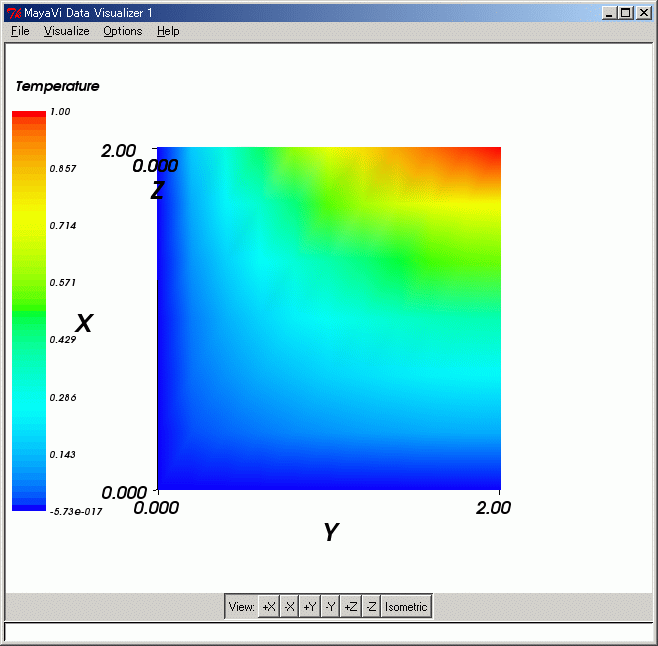
この温度分布を MayaVi で表示させます。下が上の温度分布を表示させる MayaVi フォーマット・データです。
//@@
# vtk DataFile Version 2.0
Structured Points example.
ASCII
DATASET STRUCTURED_POINTS
DIMENSIONS 7 11 1
ORIGIN 0.000 0.000 0.000
SPACING 0.333 0.200 0.000
POINT_DATA 77
SCALARS Temperature float
LOOKUP_TABLE default
-5.72533e-017 0 0 0 0 0 0
0 0.0263525 0.0479307 0.0624282 0.0859634 0.116998 0.156434
0 0.0417259 0.0823771 0.121672 0.169527 0.231056 0.309017
0 0.0564347 0.120133 0.175752 0.248643 0.339292 0.45399
0 0.0712809 0.146021 0.226142 0.321092 0.439088 0.587785
0 0.0837949 0.172039 0.270005 0.385599 0.527962 0.707107
0 0.0946571 0.194974 0.307517 0.440513 0.603811 0.809017
0 0.103545 0.213681 0.337784 0.48464 0.664793 0.891007
0 0.110128 0.227482 0.360002 0.51695 0.709441 0.951057
0 0.114168 0.235935 0.373574 0.53666 0.736671 0.987688
0 0.11553 0.238781 0.378138 0.543285 0.745823 1
//@@@
//copy \#####.### ex.vtk /y
//start mayavi -d ex.vtk
このような表示となります。