sf による相対性理論

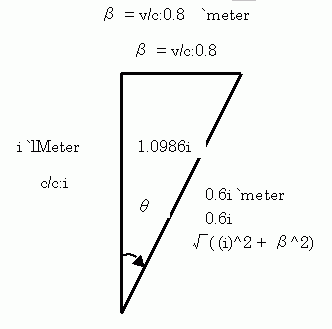
相対性理論は、自然法則を四次元時空間で記述する事により、自然を統一的に綺麗に説明してくれます。

でも数式の壁が相対性理論の理解を難しくしています。数式の意味を理解することで躓いてしうために相対性理論の綺麗さを感ずるところまで到達することが困難です。でも sf によって数式の壁を乗り越えられます

sf を使えば数式を簡単に計算できます。グラフ化できます。相対性理論で出てくる数式の数値シミュレーション実験が短単にできます。数値実験により、ともすれば無味になってしまう数式を、意味のある物理法則の表現手段として楽しみながら学んでいけます。

この web page では相対性理論の美しさを sf による数値シミュレーション実験を通して示すことを目標とします。御自分でも sf を使って計算をしながら／グラフを書かせながら読んで下さることを希望します。単に読んだり見たりしているだけよりも楽しめるはずです。

近頃の「相対性理論は誤っている」論について

近頃「相対性理論は誤っている」との説明が目に付きます。そのような本が商業出版されてさえいます。相対性理論を超える理論を示すことで「相対性理論は誤っている」と主張するならば納得できますが、多くの場合屁理屈を捏ねているようにしか見えません。これらでベクトル・ポテンシャルの話が出てくることはありません。ベクトル・ポテンシャルなどは理解できずに相対論を批判しているように見えます。

相対性理論におけるベクトル ポテンシャルの扱いの綺麗さを味わってもらいたいものと考えます。「相対性理論は誤っている」のような本が商業出版されていることは、相対性理論の美しさが理解されていないためだとも思います。

もしニュートンが現在に蘇ったとしたも決して「相対性理論は誤っている」などとは言わないでしょう。逆に相対性理論を取り込んだ統一理論を作りあげてくれそうです。アインシュタインよりニュートンのほうが頭が良さそうだからです。

「相対性理論は誤っている」論を読むより、この web page で sf を使いながら遊んでください。こちらの方が相対性理論を面白く学べるはずです。実務でも役に立つ知識を得られるはずです。

1 Lorentz 変換

1-1 Maxwell 方程式と光速度不変

Maxwell 方程式は光速度が一定値

    `c `meter/`sec
    < 2.99792e+008 >    

sf 式

ここでブロックの左上に sf expression と書いてある式は、sf で計算可能な式です。各行の式を引用符 " で囲って sf "`c `meter/`sec" などと Windows コンソールで 実行させれば計算できてしまいます。計算結果はコンソールに表示されるとともに wデフォルト変数 _dt.val に残ります。sf " exmpla=3+4&2uot などと左辺値の変数名があるときは 拡張子 ".val" を追加した example.val ファイルに計算結果が残さります。この計算結果のファイル example.val は次回の sf 式の変数として使えます。

またブロックの左上に sf block と書いてあるしきは sf でブロック計算可能です。//@@ から //@@@ の間の sf 式を temp.se ファイルなどにコピーし、コンソールから sf @@temp と実行させられます。

WZ エディタのユーザーならば kShell を使うことで引用符で囲んだり sf を追加したりする temp.se を作ったりする手間なく、sf 式の位置にカーソルを置いて ctrl O + n, ctrl O + S でマクロを実行させるだけで計算ができてしまいます。

sf.exe は単なる DOS コマンド・プログラムです。レジストリなどのコンピュータ設定を変更することはありません。sf が不必要になったときは、ファイルを delete するだけで元に戻ります。ぜひとも sf を使って計算を確認しながら以下を読み進んでください。式を追っているだけのときより効率よく理解できるはずです。評価版をこちらからダウンロードできます。

ニュートン力学の立場にたてば、Maxwell 方程式が成立する、すなわち光速度が c である絶対座標系が存在することになります。その前提としての座標系に依存しない絶対時間パラメータが存在することになります。

でも Michelson-Morley の実験では座標系による光速度の変化は観測されませんでした。ニュートン力学が間違っているならば、どう考え直すべきでしょうか。考え方を逆にして、全ての慣性座標系で Mawell 方程式などの物理法則は同じであると考えましょう。Maxwell 方程式は全ての慣性座標系で成り立つとしましょう。そうすれば Michelson-Morley の実験は説明できます。その代わり絶対時間はあきらめねばなりません。時空間座標系自体の再構築が必要になります。

以下 Maxwell 方程式から導かれる光速度不変を前提に、互いに等速度で移動している二つの慣性座標における時空座標の変換法則：Lorentz 変換を、光速度が慣性座標系によらず一定であることから導きます。まず、その前提となる四次元時空でのイベントの座標について考察します。

1-2 時空イベントの四次元座標

光の球面波を使って四次元時空イベントの慣性座標系における値：時刻 t と位置 x,y,z を決める方法を考えてみます。

何らかのイベントが発生したとき、そのイベントが発生した同じ時刻と位置で光の球面波を発生するものとします。イベントが発生する物理系にくくりつけたストロボをイベントに同期して発光させることで実現できます。このイベントを静止した座標系 S と S に対して等速度で移動している座標系 S' とで測定して比較してみましょう。

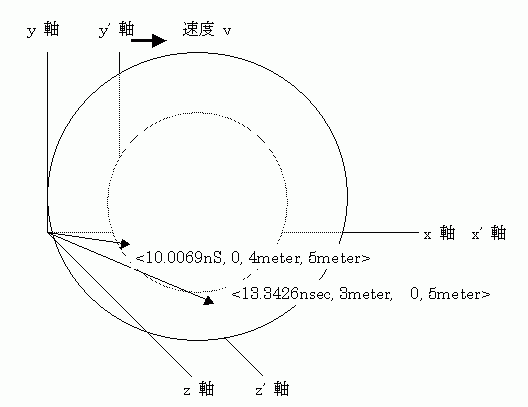
座標系 S の 時刻 0 に x, y, z 座標の位置 r

    r = <3`meter, 4`meter, 5`meter> 
< 3, 4, 0 >

この球面波は、最初に y,z 平面上の

    r_yz =<       0, 4`meter, 5`meter>
< 0, 4, 5 >

    t_yz = (3`meter/`c)/`nS
< 10.0069 >

同様に z,x 平面 r_zx の位置に時刻 t_zx nS に球面波の先端が到着します。

    r_zx =< 3`meter,       0, 5`meter>
< 3, 0, 5 >
    t_zx = (4`meter/`c)/`nS
< 13.3426 >

                 ------------------ 図 1-2. 1 --------------------

逆に

    < t_yz, r_yz> == < < 10.0069`nS,       0, 4`meter, 5`meter>
    < t_zx, r_zx> == < < 13.3426`nS, 3`meter,        , 5`meter>

<t_yz, r_yz>の測定値を得た観測者は、< ?, 4`meter, 5`meter> の位置でイベントが発生した事が解ります。さらに <t_zx, r_zx> の x 成分より < 3`meter, 4`meter, 5`meter> の座標位置でイベントが発生した事が分かります

    10.0069 - (3`meter/`c)/`nS
< -2.28559e-005 >  # 誤差範囲内で 0 nS

    13.3426 - (4`meter/`c)/`nS
< 3.61921e-005 >  # 誤差範囲内で 0 nS

さて、ここで座標系 S と時刻 0 では重なっているが x 方向に速度 v の等速度(例えば光の 80% の速度）

    v = 0.8`c
< 2.39834e+008 >
    β= v/`c
< 0.8 >

このように慣性系に対するイベントの四次元時空座標を定義することで、時刻が絶対時間としてのパラメータではなくなります。空間に散らばっていて座標系ごとに異なりうるものになります。同じイベントであっても位置だけではなく時刻も座標系ごとに異なりうる事になります。この座標系の間の変換関係を表すのが Lorentz 変換です。

1-3 Lorentz 変換行列

S, S' 二つの座標系での同一イベントに対する四次元時空座標を <t,x,y,z>, <t',x',y',z'> とします。S, S' どちらの座標系でも光速度が `c 一定である事から下の関係が成り立ちます。

    (`c t)^2 - x^2 + y^2 + z^2 == 0  <==> (`c t')^2 - x'^2 + y'^2 + z^'2 == 0

//@@
    t=1, x=1, y=1, z=1
    t' = (t- v/`c^2 x)/!sqrt(1-β^2)    # --------------- 式(1-1. 1)
    x' = (x - v t)/!sqrt(1-β^2)
    y'= y
    z'= z
//@@@

CommandFile:temp.se line:2   t' = (t- v/`c^2 x)/!sqrt(1-β^2)
    ・
    ・
< 1.66667 >
CommandFile:temp.se line:3   x' = (x - v t)/!sqrt(1-β^2)
    ・
    ・
< -3.99723e+008 >
CommandFile:temp.se line:4   y'= y
 sf command argment: y'= y
< 1 >
CommandFile:temp.se line:5   z'= z
 sf command argment: z'= z
< 1 >

v が高速の 8 割:0.8`c と早かったので t = 1 秒での x' の位置は光速度定数に近い大きな値になってしまいます。t を 1 ナノ秒と短い値にしてみます。

//@@
    t=1`nS, x=1, y=1, z=1
    (t' = (t- v/`c^2 )/!sqrt(1-β^2) ) 1/`nS
    x' = (x - v t)/!sqrt(1-β^2)
    y'= y
    z'= z
//@@@
CommandFile:temp.se line:2   (t' = (t- v/`c^2 )/!sqrt(1-β^2) ) 1/`nS
    ・
    ・
< -2.78085 >
CommandFile:temp.se line:3   x' = (x - v t)/!sqrt(1-β^2)
    ・


    ・
< 1.26694 >
CommandFile:temp.se line:4   y'= y
 sf command argment: y'= y
< 1 >
CommandFile:temp.se line:5   z'= z
 sf command argment: z'= z
< 1 >

この例のように sf を使うことで、Lorentz 変換の式が、単なる公式ではなく、計算可能な式にもできます。途中の計算結果は t.val, t'.val, x.val, x'.val などの sf 変数ファイルとしてカレント ディレクトリに残っています。

type t.val
% BaseDouble 1
< 1e-009 >

type t'.val
% BaseDouble 1
< -2.780854602642028e-009 >

type x.val
% BaseDouble 1
< 1 >

type x'.val
% BaseDouble 1
< 1.266943389333334 >

カレント ディレクトリに残してある t,t',x,x' などの変数は、下のように何時でも再利用できます。s^2 = -(c t)^2 + x^2 + y^2 + z^2 が Lorentz 不変であることなどを思いつくままに実験計算できます。光速度 `c のように物理定数を MKSA 単位系定数の値を持つ定数変数として計算可能です。さらに時間を `nS を使って計算したように、物理単位系を含んだ計算も可能です。これらの計算結果のグラフ表示も簡単です。

(-(`c t')^2 + x'^2 + y'^2 + z'^2) - (-(`c t)^2 + x^2 + y^2 + z^2) 
< 1.33227e-015+1.70225e-016i >
# <== マイナス値の自乗計算が入るので計算結果に誤差虚数が入ります。e-15, e-16 オーダーの数値計算誤差は入り込んでいます。

sf を使って計算／グラフ化しながら物理法則を記述する数式を追求していくことで、数式の意味／物理法則を理解しながら教科書や論文を読み進んでいけます。ぜひとも、御自分でも数式を計算しながら、パラメーターを自分の興味のある値に変えたりしながら、以下を読み薦めてください。

1-4 Lorentz 変換と直角三角形のピタゴラスの定理

Minkowsky 空間での幾何学の視点から見ると、Lorentz 変換は直角三角形のピタゴラスの定理を虚数空間にまで拡張したものと見なせます。

式(1-1. 1)で時間要素を t を `c t にします。x と `ct を同じ物理次元にします。下のように変形できます。

            ( ~c t- v/`c x)     (`c t- β x) 
   `c t' == --------------- == --------------
            !sqrt(1-β^2   )    !sqrt(1-β^2)

                   1                    β
         == -------------- `c t - --------------  x
             !sqrt(1-β^2)           !sqrt(1-β^2)


             (x - v t)                      
    x'   == ---------------                 
             !sqrt(1-β^2)                  
         
                -β                   1
         == --------------`c t + --------------  x
            !sqrt(1-β^2)          !sqrt(1-β^2)

1/!sqrt(1-β^2)
< 1.66667 >
β/!sqrt(1-β^2)
< 1.33333 >

Minkowsky 空間は時間軸を虚数とする座標系です。`c t を i `c t にすると、上の式は下のように変形されます。

                   1                   i β
 i `c t' == -------------- i `c t - --------------  x
             !sqrt(1-β^2)          !sqrt(1-β^2)

                   i                     β
         == -------------- i `c t + --------------  x
            !sqrt(-1+β^2)          !sqrt(-1+β^2)

                 i β                     1 
    x'   ==  --------------i `c t  + --------------  x
             !sqrt(1-β^2)           !sqrt(1-β^2)

                   β                     i 
        == - --------------i `c t  + --------------  x
             !sqrt(-1+β^2)           !sqrt(-1+β^2)


                │         i                β        │
< i `c t, x> == │ -------------- ,   --------------  │< i `c t, x> ---- 式(1-4. 1)
                │ !sqrt(-1+β^2)      !sqrt(-1+β^2) │
                │                                    │
                │         β                 i       │
                │- -------------- ,   -------------- │ 
                │   !sqrt(-1+β^2)    !sqrt(-1+β^2) │

1/!sqrt(-1+β^2)
< -1.66667i >
β/!sqrt(-1+β^2)
< -1.33333i >

この行列は下のような複素係数の Lorentz 変換行列になります。

< i `c t', x'> = │ 1.66667, -1.33333i│ < i `c t, x> ------------------- 式(1-4. 2)
                 │1.33333i,  1.66667 │

式(1-4. 1) は、下のような回転行列に良く似ています。

//@@
@@subVar Rotate2 2,2
    < !cos(θ),-!sin(θ)> # --------------------------------------------- 式(1-4.3)
    < !sin(θ), !cos(θ)>
@@endSubVar
//@@@

実際に下のように回転角度を求めると、回転角は虚数値になりますが、その回転行列は式(1-4. 2) と同じ要素値になります。

θ=!asin(-β/!sqrt(-1+β^2) ) # ----------------------------------------- 式(1-4.4)
< 1.09861i >

Rotate2.var
<   1.66667, -1.33333i >
<  1.33333i,   1.66667 >

式(1-4. 1) (1-4. 3)は数のように一秒(虚数時間 i sec) 進んだときに x 方向に β== `v/`c だけ進む直角三角形の関係とも見なせます。斜辺は虚数になってしまっており、Minkowsky 空間での三角形ですが。

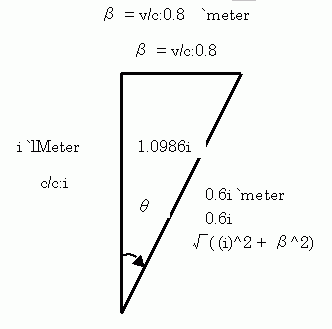
                 ------------------ 図 1-4. 1 --------------------

`lMeter 光メーター

ここで新しい時間の単位 `lMeter 光メーターを導入しておきます。1`lMeter は 1 光メーターの意味、光が 1`meter を通過するのに掛かる時間の意味です。`meter と同じ物理量ですが、時間単位であることを明確にするために使います。a=3`lMeter と書けば、変数 a は時間であることが明確になります。

時間を `lMeter で表した単位系では光速度定数 `c が 1 の値になります。1`lMeter の時間は 3.3`nS ナノ秒 3.3e-9 秒と同じ時間です。

この単位系で解釈した上の直角三角形の意味は、時間が 1`lMeter 進んだときに x 軸方向に 0.8`meter 進んでいるとの意味になります。

この虚数回転角は、座標系の相対速度が光速度( βが 1 )に近づくとともに、無限に増えていきます。

N@=100, <<0,N,1/N @β|!asin(-β/!sqrt(-1+β^2) ) >>
!image(_dt)

gdsp

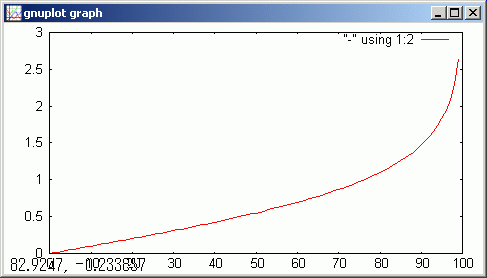
Lorentz 変換を Minkowsky 空間での虚数回転とみなすことで、相対論でのシミュレーション計算の見通しが良くなります。式(1-4. 3) の回転行列を表す sf サブ・バリアブル変数一つで、Euclid 回転と Lorentz 回転の両方を扱えます。