元利均等払いは毎月の返済金額が一定になる借入金の返済方式であることは誰でも理解していると思います。でも数式を使うような詳しい説明はあまりなされません。自分でシミュレーション計算をしようとして調べてみましたが Web 上で的確なものを見つけられませんでした。ここの銀行協会の計算例から逆推論することで元利均等払いの数式を導きました。
解ってみれば、元利均等払いの理論は簡単です。高校数学の等比級数の応用問題にすぎません。どうも、文系の人は数式で考えようとしないようです。標準例の表を示して中途半端に言葉で説明しようとします。黙って銀行が計算した通りに利子を付けて返済するように仕向けているとも勘ぐりたくなります。
理系で数式が扱える方にとっては、以下の数式を使った説明のほうが先の銀行協会の説明より、元利均等払いを短時間に・簡単に・完全に理解できるはずです。そして sf 電卓ソフトを使えば、望むままの返済シミュレーションができるようになります。同時に、以下の説明を読むことで、元本金額の変化などの何十もの数値を一つのベクタとして扱う sf の便利さを体感できます。それを金利計算以外の多方面に活用できるようになります。そのために必要な時間は、金利シミュレーションソフトのマニュアルを読んで理解する時間より短いはずです。損はしません。以下の説明にお付き合い願います。
解りにくい元利均等払いを論ずる前に、単純な事例を考えてみましょう。借りたお金を一ヶ月後の一回だけの返却で済ますときは話は簡単です。
年利 23 % とし、10 万円の金額を借りたとします。借り入れ金額 T と月利 r を下のように置きます。
T = 10`man # 借り入れ金額 10 万円 < 100000 > r = 0.23/12 # 月利 < 0.0191667 >
一ヶ月あとに返却する金額は下のようになります。
I = T r # 利子:Interrest 分 < 1916.67 > P = T # 元本:Original Principal < 100000 > I + P # 返却金の総額 == 利子 + 元本です < 101917 >
借りたお金を 12 ヶ月後に一回だけの返却で済ますととすると、金利が複利で利いてくるため少し複雑になります
T (1+r)^12 # 返却金の総額です < 125586 >
変です。年利 23% ならば一年後に返す金額は T*1.23 のはずです。r = 年利/12 としながら、それを複利で計算して T(1+r)^12 としたところに誤魔化しがありました。うっかりしていると
T (1+r)^12 - T 1.23 # 誤魔化されて余分に取られる金額 < 2586.38 >の金額 2586 円をを余分に取られてしまうところでした。
残念ながら、現実の元利均等払い方式は上の誤魔化しをさらに巧妙に実行しています。大部分の方は元利均等払いの計算の面倒さのために、この誤魔化しに気づかないままに余分なお金を返却させられています。この巧妙な誤魔化しにも注目しながら元利均等払いの説明を読んでいって下さい。
sf 式ここでブロックの左上に sf expression と書いてある式は、sf で計算可能な式です。各行の式を引用符 " で囲って sf "I = T r # 利子:Interrest 分" などと Windows コンソールで 実行させれば計算できてしまいます。計算結果はコンソールに表示されるとともに T.val などと左辺値の変数名に拡張子 ".val" を追加したファイル名にも残されています。この計算結果のファイル T.val は次回の sf 式の変数として使えます。
WZ エディタのユーザーならば kShell を使うことで引用符で囲んだり sf を追加したりする手間なく、sf 式の位置にカーソルを置いて ctrl O + n でマクロを実行させるだけで計算ができてしまいます。
sf.exe は単なる DOS コマンド・プログラムです。レジストリなどのコンピュータ設定を変更することはありません。sf が不必要になったときは、ファイルを delete するだけで元に戻ります。ぜひとも sf を使って計算を確認しながら以下を読み進んでください。式を追っているだけのときより効率よく理解できるはずです。評価版をこちらからダウンロードできます。
複利計算は高校の数学でやる等比級数の計算にすぎません。でも元利均等払いでは、何十ヶ月もの複利計算が必要になります。複利計算によって毎月の金利分と元本返済分が計算されますが、金利分と、元本返済分は月ごとに変わっていきます。電卓計算では手間がかかりすぎます。
sf ならば何十ヶ月もの複利計算を一つの数値ベクトル変数として一つの計算式で処理できます。等差数列や等比数列を一つの sf 式で記述できます。元利均等払いの金利計算のために、ここで sf による等差数列や等比数列、また数列の部分和の計算のしかたを見ておきましょう。
sf ではベクタを数値の並びとして<1,2,5,8>, <3.1, 2.5, 10.8, 5.1.3,3> などののように < と > で囲まれた数値列として表現します。この数値列は sf によりベクタ演算可能です。
<1,2,3,4,5> + <1,1,1,1,1> < 2, 3, 4, 5, 6 > # 計算結果のような具合です。
sf では規則性のあるベクタ:数値列をを <<.sf 数列表現規則...>> によって短く表現できます。まず一番単純な等差数列は、<< 初期値, サイズ, 公差>> のように、表現できます。
<<1,10,2>> < 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 &g; # 計算結果上の例は、初期値が 1 で、10 個の値からなる、要素ごとの差分が 2 の数列を sf 式として表しています。等比数列などのより複雑な数列は、上の式をもう少し複雑にした
<< 初期値, サイズ, 公差& @ parameter| parameter に依存する sf 式>>によって表します。parameter 変数には、初期値/サイズ/公差より定まる等差数列が順次設定されます。
<<0, 10, 1 @ k | 3*2^k >> < 3, 6, 12, 24, 48, 96, 192, 384, 768, 1536 > # 計算結果 a@=3,r@=2,<< 0, 10, 1 @ k | a r^k >> # 上の sf 式と同じ意味となる sf 式です。 < 3, 6, 12, 24, 48, 96, 192, 384, 768, 1536 > # 計算結果上の用に << 0, 10, 1 @ k | 3*2^k >> の sf 式により、初期値が 3、サイズが 10 で、公比が 2 の等比数列が作られました。
テンポラリ変数a@=3,r@=2,<< 0, 10, 1 @ k | a r^k >> で出てくる a@=3 などの sf 式は「temporary 変数 a に 3 を代入する」との意味です。変数名が @= の左側に記述されることで、「メモリ上に一時的に設定される変数に 3 を代入する。ファイル変数に代入するのではない。」の意味になります。ファイル変数への書き込みがなくなるので、高速に計算できます。ディレクトリ内に余分な sf 計算結果を残さずにすみます。
(sf ベクタ)[index] により、index の位置にあるベクタ要素を取り出せます。さらに拡張して (sf ベクタ)[<start, size, stride>] sf 式により、start, size, stride より定まる等比数列に相当する部分の数列部分列を取り出せます。また !sum(sf ベクタ引数) 関数により数列全部要素の全部を足し合わせたスカラー値を計算できます。
vector = <<1,10,2>> # 等比級数ベクタを vector 変数に設定します < 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 > # 計算結果 vector[0] # vector の 0 番目の要素を求めます < 1 > # 計算結果 !sum(vector) # vector 要素全てを足し合わせます < 100 > # 計算結果 vector[<1,3,2>] # vector ベクタより 1,3,5 要素を取り出します。 < 3, 7, 11 > # 計算結果 <<1,10,2>>[<1,3,2>] # 上の部分数列の取り出しを一つの sf 式で実行させます < 3, 7, 11 > # 計算結果
10 万円の金額を月利 23/12 % で借りて n=20 ヶ月あとに、または 30 ヶ月あとに一括返済するとき、複利での利子を足し合わせた返済金額は次のように 14.6 万円、17.7 万円と計算できます。
hensaiVct=(P@=10`man, r=0.23/12, N=100, << 0,N,1@k|P (1+r)^k >> < 100000, 101917, 103870, 105861, 107890, 109958, 112065, 114213, 116402, 118633 , 120907, 123225, 125586, 127993, 130447, 132947, 135495, 138092, 140739, 143436 , 146185, 148987, 151843, 154753, 157719, 160742, 163823, 166963, 170163, 173425 , 176749, 180136, 183589, 187108, 190694, 194349, 198074, 201870, 205740, 209683 , 213702, 217798, 221972, 226227, 230563, 234982, 239486, 244076, 248754, 253522 , 258381, 263333, 268381, 273524, 278767, 284110, 289555, 295105, 300761, 306526 , 312401, 318389, 324491, 330711, 337049, 343509, 350093, 356804, 363642, 370612 , 377715, 384955, 392333, 399853, 407517, 415328, 423288, 431401, 439670, 448097 , 456685, 465438, 474359, 483451, 492717, 502161, 511786, 521595, 531592, 541781 , 552165, 562748, 573534, 584527, 595730, 607149, 618786, 630646, 642733, 655052 > hensaiVct[20] < 146185 > hensaiVct[30] < 176749 >
準備完了です。いよいよ sf によるベクトル:数列の扱いを活用して、計算式元利均等払い方式について見ていきます。
元利均等払方式とは、元本と金利と返済回数から、次回に返却する元本返済金額と返済利子額の二つを決める方式です。この元利均等払方式を数式を使って定義します。そして毎月の返済額が一定になるように、利子返済分と元本返済分それぞれが合理的に決められていることを見ます。この数式の意味を理解する事が元利均等払い方式を理解することです。この数式を理解できれば、後は sf 式を使って自由に返済シミュレーションができるようになります。
返済金額を決める計算式を記述するときに前提となる変数と、その意味を下のように定義します。
T = 10 `man # 借入金 10 万円 < 100000 > r = 0.23/12 # 月利(1 より小さい実数 -- 年利 23% のとき r=0.23/12=0.019) < 0.0191667 > RM =1+r, # 月あたりの元本の増加係数( 1 より大きい実数。年利 23% のとき 1.019) < 1.01917 > n = 15 # 返済月数 15 ヶ月で返済するものと仮定します < 15 >RM 変数と r 変数の違いは 1 の差だけです。どちらも利率を示す変数です。計算式が単純になるほうを適宜選択します。
さて元利均等返済で求められる元本分と、利子分の返済金額の変数 P,I を下のように定義します。
・ Pj:principal_repaid:月額の元金返済額 ・ Ij:interrest:月額の利息支払額 ここで j は何回目の返済であるかを示す番号とします。
すると初回( 0 回目)の元利均等払いでの初回の返済利子と、返済元本の金額は下の式で計算されます。
I0 = T r # 利息分interrest -------------------------------------------- (1) 式 < 1916.67 > # 毎月 P0 円の金額を n ヶ月返したとき、複利合計計算で T 円になるように P0 を決めます P0 = T (1-RM)/(1-RM^n) # 毎月の元本返済分 ----------------------------- (2) 式 < 5817.44 > # 利子と元本返済分の両方を足して求めた、一月後の返済額 I0 + P0 < 7734.11 > ---------------------------------------------------------- (3)式(1)式は借入金に利子を掛けただけの利息分を示す単純な式です。最初に返済する金額の利子分 I0 は、借り入れ金額 T に月利 r を掛けたものです。(2) 式は少し複雑ですが、その意味は下の等比級数の和の公式から逆算して、毎月の元本分の返済額を計算しているだけです。
P0*(1-RM^n)/(1-RM) # T == P0 + P0*RM + P0*RM^2 + ... + P0*RM^(n-1) ---- (4)式すなわち、毎月支払い利子と同じ利息で P0 の返済額を複利計算で n ヶ月返却したとき、ちょうど借り入れ金額 T 円になるように、初回の元本返済分 P0 が定められます。
一回目の月の I0,P0 の返済の後には元本は T-P0 に減っています。T-P0 より、次の月の利子と元本の返済額 I1,P1 が下のように計算できます。
I1 = (T-P0) r # 金利分 < 1805.17 > P1 = (T-P0)( (1-RM)/(1-RM^(n-1) ) ) # 返済分 < 5928.95 > I1 + P1 < 7734.11 &6gt;上の式は、元本が T-P0 に少なくなったものとして I1, P1 を (1),(2) 式を適用したものです。
ここで、利息分と元本両方の返済金額について I0+P0 == I1+IP1 が成り立ちます。この代数関係は任意の Ij, Pj について成り立ちます。すなわち (3) 式の毎月の返済額一定であることが分かります。一回目より元本が減ったことにより金利の減少分が、残りの返済回数が少なくなったことによる元本返済分の増加額で打ち消しあうことになります。sf で元本、金利、返済回数を様々ときの I0,P0, I1,P1 を計算していみれば、このことを確認できます。これが元利均等払いと「均等」の説明が入る理由です。
より厳密には付録の代数計算で証明できます。
毎月の返済額だけを計算するのならば、(1)式と(2)式を足し合わせて初回の返済額を計算するだけであり、簡単な電卓計算だけですみます。総返済額の計算も (3) 式に n を掛けるだけで計算できます。でも、途中での一括返済や、安い金利に借り換えるためのシミュレーション計算をしようとすると、それまでの元本返済分 P0 + P1 + ... + Pj の計算が必要になります。返済回数 j が 10 を超えてきたら電卓では計算するには手間が掛かりすぎます。プログラムを作ったりして計算します。そのためのソフトもシェアウェアなどで多く配布されています。でも sf を使えば P0,P1,...Pn-1 が自分で簡単に計算できます。プログラムを作るまでもなく、借り換えの返済シミュレーションができます。
1000万円を年利 5% 10 年で借りた場合の元本の減り方を 12*10==120 サイズの数値ベクタとして計算します。以下の計算は、ご自分で実際に sf を使って計算させながら読んで下さることを希望します。途中経過での詳細な数値も
n=10*12, r=0.05/12, T=1000 T@=1000,R@=1+r,Principal = <<0,n,1@j| T|,T=T(1-(1-R)/(1-R^(n-j)))>> # ↑ "|," 記号によってベクタ要素を計算前の T の値にします。
確認の意味で、毎月の利子返済分、元本返済分を計算してみます
R@=1+r,Principal_repaid = <<0,n,1@j|Principal[j](1-R)/(1-R^(n-j))>> Interrest = Principal r monthly_repaid = Principal_repaid + Interrest # 毎月の返済額は 10.6066 円と一定です !sum(monthly_repaid) # 総返済額 < 1272.79 > # !sum(monthly_repaid)の計算結果Principal.val ベクタ数値データをグラフ表示するためには、コンソールで下の gdsp バッチ・コマンドを使って gnuplot に表示できます。
gdsp.bat Principal
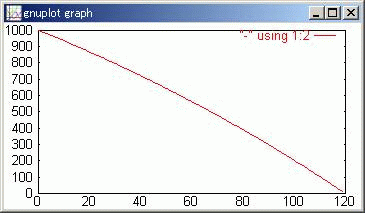
下の sf 計算により、返済期間の半分の 5 年が経過した時点での元金が
Principal[5*12] < 562.049 >半分の 5 年が経過した時点で元金は 44% 弱だけ減っていることが解ります。50% の 500 万円ではありません。
半分が経過した時点で、残債を一括返済したとき、562 万円の返却が必要です。それまでに支払った金利分の合計は下のようになります。
!sum(Interrest[<0,12*5,1>]) < 198.442 >トータルで利息も含めた返済分は 1198万4420円になります。
ここで 5 年目に 4 % の金利 5 年均等払いの融資に借り替えたときのシミュレーションをしてみます。計算式を下に示します。上の計算で 5 年経過した後に 562万490円のの元本が残っていることを使います
n=5*12, r=0.04/12 T@=562.049,R@=1+r,Principal4 = <<0,n,1@j|T|,T=T(1-(1-R)/(1-R^(n-j)))>> Interrest4 = Principal4 r !sum(interrest4) < 59.0103 > !sum(Interrest[<12*10/2,12*10/2,1>]) - !sum(interrest4)" < 15.3342 >約 15 万円の差額だけ特をすることになります。実際には手数料や手間隙がかかるので、それらを差し引いて借り換えの可否を判断することになります。
月利 mr を年利 yr から mr = yr/12 で計算していましたが、厳密には月利は複利で計算するべきでしょう。月ごとに返済するならば、年末までの期間分の金利が付くべぎてす。複利だとすると月利と年利の間に、下の関係がなりたちます。
1+yr == (1+mr)^12これを使って、下の様に複利/単利計算をしたときの月利を計算できます。
yr@=0.05, mr=(1+yr)^(1/12)-1 # 複利での月利 < 0.00407412 > 0.05/12 # 単利での月利 < 0.00416667 >
5% の年利のとき、0.00017 程度の違いがでてきます。この違いを、1000 万円を 20 年 5% で借りたときで計算してみます。下の計算のように、約 15 万円程度の違いが出てきます。先の 4% への借り換えによる差額と同程度の大きな金額です。
T@=1000, R@=1+mr, n=20*12, T( R-1 + (1-R)/(1-R^n) ) n # 複利月利での総返済額 < 1569.21 > T@=1000, R@=1+0.05/12, n=20*12, T( R-1 + (1-R)/(1-R^n) ) n # 単利月利での総返済額 < 1583.89 >
実務の元利均等払いの計算では、貸し手側が得をする単利での月利を使うのが慣習になっているようです。先の銀行協会での pdf での計算例も、単利で計算しています。元利均等払いについて、ここで行っているような数式を使った真っ当な説明していないのは、このインチキがばれないようにするためかと勘ぐりたくなります。
昭和 55 年に単利換算での元利均等払いの年利表示が不当であると国会でも論じられています。下に、その記事録があります。
http://kokkai.ndl.go.jp/SENTAKU/sangiin/093/1380/09310131380001c.html
sf 自体は登録料 5000 円のソフトですが、一ヶ月以内でしたら無料で使えます。簡単に試せます。使うためには、パスの通ったディレクトリに zip ファイルを解凍するだけです。解凍したさきをカレント ディレクトリとして使えばパスの変更も必要ありません。レジストリ変更などのコンピュータを汚すことはしません。
sf の使い方も簡単です。数式も扱える関数電卓の感覚で使えるはずです。理系の方にとっては、たぶん Excel の PMT 関数を使った方法を調べるよりも sf で等比級数の計算をしたほうが簡単でしょう。(PMT 関数についても EXCEL では数式での説明は殆どありません。公式を使えというだけです。)この sf の使い道はローン計算に限りません。多方面に使えます。理系の方にとっては便利なツールになるはずです。ぜひお試しください。そして気に入ったら登録願います。
P1+I1 == (T-P0)( -(1-R) + (1-R)/(1-R^(n-1)) )
== (T-P0)( R-1 + (1-R)/(1-R^(n-1)) )
== T( 1- 1/( (1-r)/(1-r^n ) ) )*( r + (1-r^(n-1))/(1-r) )
== T( (( R^(n+1 - R^n) )/(R^n -1) )
== T( r + (1-R)/(1-R^n) )
== I0 + P0