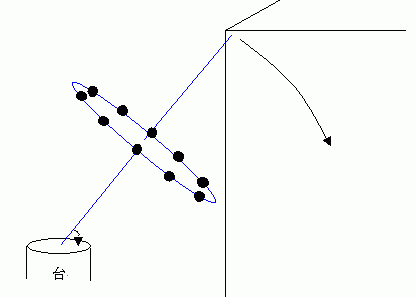
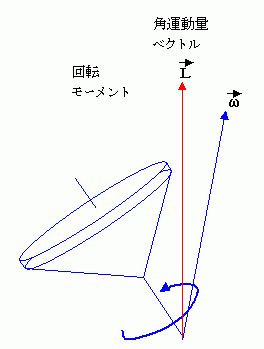
独楽が倒れないことは
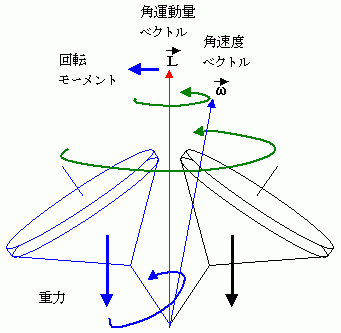
歳差運動は、独楽を倒そうとする力の時間平均を 0 にします。角運動量と独楽の高速回転によって、独楽の倒れる速度が極端に遅くなっているので、少し倒れる間に独楽の回転軸は何回も回ります。 独楽を倒そうとする重力の回転モーメントは、回転軸が一回転する間に独楽を左側に倒そうとしたり右側に倒そうとしたりします。 回転モーメントの時間平均は、一回転する間に 0 になってしまいます。歳差運動によって、勝手にバランスを取ってしまうことにより、独楽は倒れないわけです。
独楽が倒れないことに独楽の歳差運動が本質的な役割を果たしていることは、独楽の回転軸を途中で止めてしまう壁を置いてやると、独楽が直ぐに倒れてしまうことから確かめられます。

回転する独楽が歳差運動することは、直感的には次のように説明できます。 独楽を倒そうとする力 F は、独楽を倒す方向とは直交する向きをもつ回転モーメント・ベクトル N として働きます。この N は角運動量ベクトル L を「N*時間」だけ変化させます。この L の変化は角運動量ベクトル ω を Nの方向に変化させます。この角運動量の変移は独楽を Δy の方向に移動させます。一方で独楽の回転が速くなると角運動量 L が大きくなります。すると重力により倒れる方向の変移 Δx が小さくなります。逆に Δy は独楽の回転数に比例して増えていきます。Δy >> Δx のとき歳差運動が発生します。回転数が遅い、こまの形が不適切であるなどの理由で Δy >> Δx の条件が成り立たなくなると独楽は倒れてしまいます。
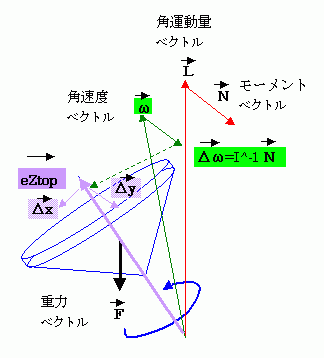
独楽の理論は回転軸と角速度ベクトルの運動を説明します。重力を受けながら高速に回転する独楽は、章動と呼ばれる小さな歳差運動行います。通常この章動は目視では判らない小ささです。独楽の回転が速くなると、章動も早くまた小さくなります。これが大きな歳差運動を引き起こします。また独楽の章動には、独楽が倒れて大きくなった Δx をブーメランのように元の高さまで引き戻す働きもあります。結果として Δx を小さくし、 Δy >> Δxを実現します。この章動の動きを正確に説明するには数式が必要になります。数式といっても、三次元での行列・ベクトルの運動方程式です。慣性テンソルを使って角運動量ベクトル・角速度ベクトル・独楽の回転軸の三つの運動を扱うだけです。高校生でも数学と物理分野で自力を持つ方ならば理解できると思います。少しばかり骨はあるかもしれませんが、独楽の運動を理解する知的散歩にお付き合いください。
なお以下の説明では sf と python による数式・数値計算を活用します。力学の教科書では「剛体の運動を表すオイラー方程式」を使ってコマの運動を説明しますが、この方程式はコマと一緒に回転する座標系での方程式であり解りにくいものです。以下で行うような、剛体のオイラー方程式を使わない、現在のコンピュータ・パワーを利用したシミュレーションによる説明のほうが独楽の運動をより良く理解できると思います。御自分でも sf や python を使って様々の場合に数値実験を広げな計算しながら読んで下さい。より面白く・深く理解できるはずです。
独楽が章動する理由は、角運動量ベクトル・角速度ベクトルと独楽の回転軸の方向が異なるためです。角運動量は保存されるのですが、独楽の回転軸が章動するためです。この回転軸の章動を扱うためには、慣性モーメントを拡張した慣性テンソルの概念が必要になります。これを使って角速度ベクトルの変化を求める必要があります。
角運動量の定義から、角運動量ベクトル L は次の行列と角運動量ベクトル ω の積で表せます。
L ≡ Σ m{k} r{k} x v{k}
k
== Σ m{k} r{k} x (ω x r{k})
k
== Σ m{k} (<r{k}|r{k}> ω - <r{k}|ω>r{k}
k
== Σ m{k} | r{k}[1]^2 + r{k}[2]^2, - r{k}[1] r{k}[0], -r{k}[2] r{k}[0] | |ω[0]|
k | -r{k}[0] r{k}[1], r{k}[2]^2+ r{k}[0]^2, -r{k}[2] r{k}[1] | |ω[1]|
| -r{k}[0] r{k}[2], -r{k}[1] r{k}[2], r{k}[0]^2+ r{k}[1]^2 | |ω[2]|
------------------------------------------- (慣性テンソルの式)
外積の公式上の式の変形で a x b x c == <a|c> b - <a|b> c の公式を使いました。この公式が納得できない方は、次の sf ブロック式で公式を試して下さい。
//@@ a@=<1,2,3>,b@=<4,5,6>,c@=<7,8,9> @op(a,@op(b,c)) - (< a | c > b - < a | b > c) //@@@ < 0, 0, 0 >このように、以下に出てくる解説や式の変形などを時分でも確認しながら読み進んでください。
なお上の sf ブロック式でコリオリの力の所で定義した外積を計算する sf サブ・ファイル op.sfを使っています。こちらも参照しておいてください。
この慣性テンソルの固有値が互いに異なるため、L == Itnsr ω の L と ω の方向がずれてきます。トルクが加わって角運動量 L が変化すると、角速度ベクトルは Itnsor^-1 (L+ΔL) と変化します。以下、慣性テンソルを実際に計算してみましょう。
慣性テンソルを計算しやすくするため、次の sf サブ・ファイル tensor.sf「単位質量が r の位置にあるときの慣性テンソル」を作っておきます。これに質量を掛けて足し合わせてやれば慣性テンソルを計算できます。
//@@
@@subFile tensorI # 単位質量が r∈R^3 の位置にあるときの慣性テンソル
_rt = [[3]]
r_ @= _prm{1}
_rt[0,*] = < r_[1]^2+r_[2]^2, -r_[1]r_[0], -r_[2]r_[0]>
_rt[1,*] = < -r_[0]r_[1], r_[2]^2+r_[0]^2, -r_[2]r_[1]>
_rt[2,*] = < -r_[0]r_[2], -r_[1]r_[2], r_[0]^2+r_[1]^2>
@@endSubFile
//@@@
直径 1`meter で円周上に、1`Kg の質点 10 個を均等に配置した時の慣性テンソル I を計算します。中心軸の質量は無視できるとします。
下の sf 式で慣性テンソルを計算できます。上で作った tensor.sf を使います。
//@@
I = [[3]]
N@=10
r @= 1`meter/2
m @= 1`Kg
<< 0,N,2`π/N @θ|\
I = I + m @tensorI(< r !cos(θ), r !sin(θ), 0>)
>>
//@@@
sf I < 1.25, -1.66533e-016, 0 > < -1.66533e-016, 1.25, 0 > < 0, 0, 2.5 >
「慣性テンソルの式」を再度よく見てみると慣性テンソルの対角成分は x,y,z 軸に対する慣性モーメントの式になっています。これにより対称性から非対角成分が 0 であると分かるときには、慣性テンソルが簡単に計算できます。
円柱など様々の形状にたいする慣性モーメントの公式が多く作られています。これらの公式を使えば、半径 0.5`meter, 10Kg の円板の慣性テンソルは下のように計算できます。
//@@ I = [[3]] R @= 1`meter/2 m @= 10*1`Kg I[0,0] = m R^2/4 I[1,1] = m R^2/4 I[2,2] = m R^2/2 //@@@ < 0.625, 0, 0 > < 0, 0.625, 0 > < 0, 0, 1.25 >
上の円板を z 軸方向に半径分 0.5`meter だけずらします。このの慣性テンソルは次のようになります。これは地球独楽の慣性テンソルと見なせます。
//@@ I = [[3]] N@=10 R @= 1`meter/2 m @= 10`Kg I[0,0] = m R^2/4 + m R^2 I[1,1] = m R^2/4 + m R^2 I[2,2] = m R^2/2 //@@@ < 3.125, 0, 0 > < 0, 3.125, 0 > < 0, 0, 1.25 >
比例係数を変えながら円板の慣性テンソルを足し合わせてやることで、垂直に立った軸対称な独楽の慣性テンソルが計算できます。これより垂直な独楽の慣性テンソルは非対角成分が 0 であること、独楽の重心が高くなるにつれて [x,x], [y,y] 成分が大きくなることが解ります。
今度はリングを斜めに傾けたときの慣性テンソルを計算します。非対角成分が 0 ではなくなります。リングの y 軸を z 軸側に 45 `degree 傾けたと考えます。次のように計算できます。
//@@
I = [[3]]
N@=10
r @= 1`meter/2
m @= 1`Kg
<<0,N,2`π/N @θ|\
I = I + m @tensorI(< r!cos(θ), r!sin(θ)/!sqrt(2), r!sin(θ)/!sqrt(2)>)
>>
//@@@
sf I < 1.25, 4.16334e-017, 4.16334e-017 > < 4.16334e-017, 1.875, -0.625 > < 4.16334e-017, -0.625, 1.875 >
-0.625 の非対角成分が出てきました。でも、この慣性テンソルを下のように座標変換によって対角化してやれば、元の対角成分 <1.25,1.25,2.5> が出てきます。
Jacobi I < 1, 0, 0 > < 0, -0.707107, 0.707107 > < 0, -0.707107, -0.707107 > < 1.25, 1.25, 2.5 >
このように、独楽が傾いたときの慣性テンソル I が求められれば、それが角速度ベクトル ω で回転しているときの角運動量ベクトルを、テンソルとベクトルの積を使って L = I ω と計算できます。慣性テンソルが 単位行列をスカラー倍したものではなくなることで、角運動量ベクトル L と角速度ベクトル ω の方向がずれてくることが分かります。このずれが章動を変化させます。
慣性テンソルを使うことで独楽の角運動量ベクトルの運動方程式:「剛体のオイラー方程式」を記述できるようになります。しかし後で行うシミュレーション計算ではこの方程式を使いません。でも、この方程式により、独楽が小さな歳差運動:章動をする性質が見えてきます。
独楽にくくりつけられた、独楽と一緒に回転する座標系から見た角運動量ベクトル ω の運動方程式を考えます。この座標系では慣性テンソルが対角化された一定値で扱い易いからです。(固定座標系で考えると、独楽の慣性テンソルは運動に伴って変化するので運動方程式が複雑になってしまいます。)逆に独楽と一緒に回転する座標系は、固定座標系から見ると角速度ベクトル ω で回転していることになります。
コリオリの力のところで論じたように、角運動量ベクトルの時間変化は、独楽に括りつけられた ω で回転している座標系では次のように書けます。
dL dL (---) == (---) + ω x L = moment vector dt space dt bodyL = I ω であることと、独楽に括りつけられた座標系では慣性テンソルが対角化されていることから次の式が成り立ちます。
Ix ωx' = (Iy-Iz) ωy ωz + ( moment x) ------------ (剛体のオイラー方程式) Iy ωy' = (Iz-Ix) ωz ωx + ( moment y) Iz ωz' = (Ix-Iy) ωx ωy + ( moment z)上で
軸対称な独楽では Ix == Iy であることから、外部モーメントが働かないとき、次の式が成り立ちます。
Ix ωx' == (Ix-Iz) ωz ωy
Ix ωy' == -(Ix-Iz) ωz ωx
ωz' == 0
∴
ωx''== (Ix-Iz)/Ix ωz ωy' # ∵ ωz'==0 ---------- (角速度の運動方程式)
== -(Ix-Iz)^2/Ix^2 ωz^2 ωx
ωy''== -(Ix-Iz)^2/Ix^2 ωz^2 ωy
この (Ix-Iz)/Ix ωz で回転する独楽の章動は、早いけれど非常に小さな動きです。その周期は独楽の回転の数分の一です。その歳差運動の振幅は、通常の独楽では 10^-5 `meter のオーダーであり人間の目では観測できません。でも独楽を倒そうとする重力の回転モーメントを与えつづけると、小さな章動が重なって、ゆっくりだが大きな独楽の回転軸の歳差運動となります。
「角速度の運動方程式」から、角運動量ベクトルが(結果として独楽の回転軸が)回転速度の数分の一で章動していることが解ります。
普通の力学の教科書では、この「剛体のオイラー方程式」をオイラー角を導入して解析的に扱います。でも、これは難しいやり方です。いくつかの独楽の定性的な性質は導けますが、独楽が倒れる様子を知ろうとすると結局シミュレーション計算することになります。以下のシミュレーション計算では、「剛体のオイラー方程式」を使わずに、変化する慣性テンソルを行列計算で求めて ω ベクトルの運動・独楽の回転軸運動を計算します。
「角速度の運動方程式」を見ていると独楽の回転軸の章動の回転方向が、 Ix と Iz の大小関係によって逆転するように見えます。でも、このようなことは発生しません。独楽の章動は Ix と Iz の大小関係とは無関係に独楽の回転方向と同じ方向に回ります。Ix と Iz は章動の周期に聞いてくるだけです。
「角速度の運動方程式」は、独楽の回転軸の歳差運動の回転方向が、 Ix と Iz の大小関係によって逆転することを主張するけれど、これは独楽に括りつけられた座標系からみたときの話です。独楽と一緒に回転している座標系からみたとき、角速度 ω の運動の回転方向が Ix と Iz の大小関係によって逆転することを主張しているだけです。静止座標系から見たときの ω および 独楽の回転軸の回る方向はどちらも一緒であり、独楽の自転の回転方向に回ります。
ここで行うシミュレーション計算では「剛体のオイラー方程式」は使いません。シミュレーション結果の確認に使うだけです。独楽の運動に伴う慣性テンソル現代の変化なんぞ、現代のコンピュータ計算能力にとっては簡単な計算です。Δt の間に
角運動量ベクトルと角速度ベクトルが一致している初期状態を考えます。そこに衝撃トルクを与えて角速度ベクトルと角運動量ベクトルにずれを生じさせ、小さな歳差運動:章動が発生することを見ます。
後での重力トルクが働いた独楽の状態と似せるために、独楽の回転軸は z 軸から x 軸方向に 10 `degree 傾いているものとします。独楽の慣性テンソルは前に計算した半径 0.5`meter 10 Kg の円板のものを使います。
ベクトルやテンソルを y 軸の周りに 10`degree 回転させる行列が必要になるので、次の Ry.sf 変数を作っておきます。
//@@
@@subFile Ry # Ry() y 軸周りの回転 no gloval variable
_rt=[[3]]
θ_ @= _prm{1} # 引数は radian 単位の回転角です
_rt[0,*]=< !cos(θ_), 0, -!sin(θ_)>
_rt[1,*]=< 0 , 1, 0 >
_rt[2,*]=< !sin(θ_), 0, !cos(θ_)>
@@endSubFile
下のように独楽の小さな歳差運動:章動の様子を sf でシミュレーション計算できます。
//@@
/s
count@, Δt@, θ@, ψ@, eZtop@, L@, N@, ωTop@, Itop@,Itnsr@
Δt = 0.0001
θ =10`degree
count =300
# eZtop は独楽の回転軸と一緒に運動する単位ベクトルです。θ 度だけ傾けます
eZtop = @Ry(-θ)<0,0,1>
# ωTop は 1000 RPM で回っている角速度ベクトルです。これも θ 度だけ傾けます
ωTop = @Ry(-θ)<0,0, 1000 2`π/`minute>
# Itop は垂直に立った円板の慣性テンソルです
Itop = [[3]]
Itop[*,*] = <0.625,0.625,1.25>
# Itnsr は Itop を θ 度だけたときの慣性テンソルです。
Itnsr = @Ry(-θ)Itop@Ry(θ)
# 角運動量ベクトル L を計算します。まだ ωTop と同じ方向を向いています。
L = Itnsr ωTop
# 衝撃トルク N を与えます。10`Kg の円板が一秒間分のトルクを一瞬にして L に追加します。
N = @op(eZtop 0.5`meter, <0,0, -20`Kg `gH> ) 1`sec
# 衝撃トルク N の追加により L と ωTop の方向がずれました。
L = L + N
# L と ωTop の方向がずれにより、ωTop,eZtop の小さな歳差運動が発生します。
trjctry=<<0,count,1 @dummy|\
eZtop|
ωTop = Itnsr^-1 L
eZtop = eZtop + @op(ωTop,eZtop)Δt
eZtop = eZtop/!norm(eZtop) # 誤差の累積を防ぐために norm 1 に再度規格化する
φ= !atan(eZtop[1]/eZtop[0])
θ=!asin(!sqrt(eZtop[0]^2 + eZtop[1]^2))
Itnsr = @Rz(-φ)@Ry(-θ)Itop@Ry(θ)@Rz(φ)
>>
//@@@
gdsp trjctry
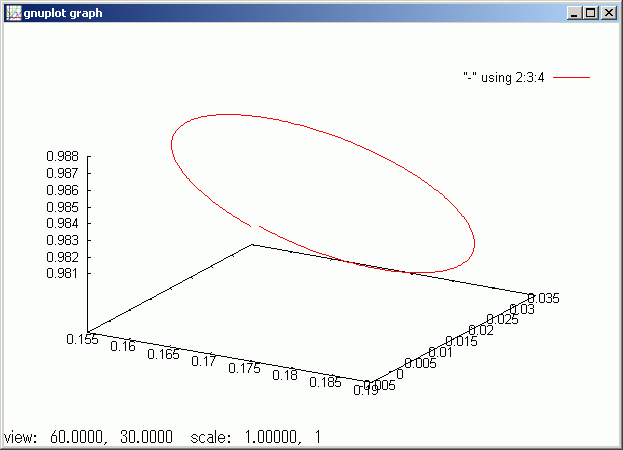
//@@ Ix @= 0.625`Kg `meter^2, Iz @= 1.25 `Kg `meter^2, ωz@= 1000 2`π/`minute 2`π/ ( (Ix-Iz)/Ix ωz ) //@@@ < -0.06 >
上のシミュレーションは衝撃トルク N Δt が加わったとき角速度ベクトルが衝撃トルクの方向に、より厳密には 慣性テンソル^-1 N Δt だけずれることを示しています。独楽を倒す重力が働いたとき、直角方向に角速度ベクトルがずれることを意味します。これが積み重なって章動が発生し歳差運動が発生します。
上でシミュレートした独楽を重力場の中に起きます。こんどは衝撃トルク N Δt が、シミュレーション刻み時間 Δt ごとに加わるものとします。N は重力が独楽に与えるトルク N = @op(eZtop 0.5`meter,<0,0, -10`Kg `gH> ) です。慣性テンソルは「z 軸方向に 0.5`meter ずらした円板の慣性テンソル」を使います
//@@
/s
Δt@, count@, θ@, ψ@, eZtop@, L@, N@, ωTop@, Itop@, Itnsr@, Rt@
Δt = 0.0001
#count=900
count=2000
Rt = [[3]]
θ=10`degree
eZtop = @Ry(-θ)<0,0,1>
ωTop = @Ry(-θ)<0,0, 1000 2`π/`minute>
Itop = [[3]]
Itop[*,*] = <3.125, 3.125, 1.25>
Itnsr = @Ry(-θ)Itop@Ry(θ)
L = Itnsr ωTop
trjctry=<<0,count,1 @dummy|\
eZtop|
N = @op(eZtop 0.5`meter,<0,0, -10`Kg `gH> )
L = L + N Δt
ωTop = Itnsr^-1 L
eZtop = eZtop + @op(ωTop,eZtop)Δt
eZtop = eZtop/!norm(eZtop) # 誤差の累積を防ぐために norm 1 に再度規格化する
# ezTop に変換する行列 Rt を作る
Rt[*,2] = eZtop
Rt[*,1] = (v@= @op(<0,0,1>,eZtop), v/!norm(v))
Rt[*,0] = @op(Rt[1,*], eZtop)
Itnsr = Rt Itop Rt^-1
>>
//@@@
gdsp trjctry

0.15 秒周期での小さな歳差運動:章動がでてきました。1`meter の回転軸の先端で 3.5`mm の振幅です。通常の 5`cm 程度のサイズの独楽では、目視では解らない動きです。
この小さな章動により独楽は倒れなくなります。重力によるモーメントにより一度は倒れた独楽の回転軸は回転エネルギーによって再度持ち上げられます。同時に角速度ベクトルは横方向に移動して行きます。
ここまでは、数式に近いまま記述できる sf 式で計算しました。計算量が少ないうちは sf での計算でも構わないのですが、独楽を一周させるような 10000 点を超える計算となると、その計算時間は一時間を越えてきます。より早いシミュレーション計算が欲しくなります。
Python を使って上の sf ブロック式を書き換えます。Python ならば、行列パッケージが備わっています。 プログラムの設計自体は sf ブロック式でなされています。これを python で実装してやれば、より高速がシミュレーション計算が実現できます。
ただし python には、外積、内積がありません。これらのルーチンを作ります。ついでに行列と array の積が行列になってしまうのも面倒なので array を返す mul(mat, array) も作っておきます。
# 外積, 行列 ベクトル 積、norm() を求める python 関数の作成
//@@
# 05.06.23 OK
# outer product function
from scipy import*
def op(arLeftAg, arRightAg): # 3 array argment and return 3 array
rt_ = zeros(3, Float64)
rt_[0] = arLeftAg[1]*arRightAg[2] - arLeftAg[2]*arRightAg[1]
rt_[1] = arLeftAg[2]*arRightAg[0] - arLeftAg[0]*arRightAg[2]
rt_[2] = arLeftAg[0]*arRightAg[1] - arLeftAg[1]*arRightAg[0]
return rt_
def norm(tplAg): # if you use mat argment, use flat
dbAt = 0
for dbElmAt in tplAg:
dbAt += dbElmAt**2
return dbAt**0.5
# multiply a mat and an array variable. This fucttion returns an array
def mul(mtAg, arAg):
_mtAt = mat(reshape(arAg, (len(arAg),1) ) )
return ravel(mtAg * _mtAt)
//@@@
//copy \#####.### op.py /v /y
次のように sf コードを python コードに移植しました。約 3 倍のサイズに大きくなります。このコード量の差は、理論を考えて試行錯誤しているときには大きな差となります。数式と殆ど同じに記述できる sf での理論式の展開は誤りの混入を防いでくれます。sf の威力が分かると思います。
python コードの大部分は sf 式の置き換えです。角速度による eZtop の Δt 秒後の変化の記述を、誤差の累積の少ないものに変更しました。コメント・アウトしてある「eZtop = eZtop + op(omegaTop, eZtop)*delta_t」を使えば sf 式と同じ数値変化になります。このように直角三角形分だけ変化させるより、円運動に沿った二等辺三角形分だけ変化させた方が誤差の累積が少なくて済みます。
また独楽の回転軸ベクトルの軌跡以外に、角運動ベクトル・重力トルク*時間・角運動量ベクトルの軌跡も出力させるようにしました。putSf(.) 関数を使って sf 行列変数として HDD ファイルに残すようにしました。こうする事により、シュミレーション結果を様々に・簡単に後で検討できます。
//@@
# 05.06.26 PM23
# -*- encoding: cp932 -*-
from sys import*
from scipy import*
from sfVal import*
from LinearAlgebra import *
from op import *
delta_t = 0.001
#delta_t = 0.0001
#delta_t = 0.00001
#count = 2000
#count =30000
count =12000
minute = 60
theta=2*pi*10/360 # 10 degree --> radian
eZtop = array([sin(theta),0,cos(theta) ])
omegaTop = array([0,0, 1000*2*pi/minute])
Rt = mat(reshape(zeros(3*3, Float64), (3,3) ))
Rt[0,:] = [cos(theta),0,sin(theta)]
Rt[1,:] = [0,1,0]
Rt[2,:] = [-sin(theta),0,cos(theta)]
omegaTop = mul(Rt, omegaTop)
Itop = mat(identity(3),Float64)
Itop[0,0] = 3.125 # Kg meter^2
Itop[1,1] = 3.125 # Kg meter^2
Itop[2,2] = 1.25 # Kg meter^2
Itnsr = Rt*Itop*Rt.I
L = mul(Itnsr,omegaTop)
trjctry = reshape( zeros(3*count,Float64), (count,3) )
omegaTrjctry = reshape( zeros(3*count,Float64), (count,3) )
Ntrjctry = reshape( zeros(3*count,Float64), (count,3) )
Ltrjctry = reshape( zeros(3*count,Float64), (count,3) )
for indexAt in range(count):
# print "eZtop:",eZtop
N = op(eZtop*0.5, [ 0, 0, -10*9.806649999999999])
L = L + N* delta_t
omegaTop = mul(Itnsr.I, L)
# ω が eZtop に引き起こす回転半径は、ωtop の単位方向ベクトルと eZtop
# との外積で定まります。回転速度には無関係です。回転速度は phi を定めます
# Δt=0.001 以下のときは eZtop = eZtop + op(omegaTop, eZtop)*delta_t を
# 使うと誤差が累積してくる
eYtop = op(omegaTop/norm(omegaTop), eZtop)
eXtop = op(eYtop, eZtop)
omegaAbs = norm(omegaTop)
phi = omegaAbs * delta_t
eZtop = eZtop + eXtop*cos(phi) + eYtop*sin(phi) - eXtop
#eZtop = eZtop + op(omegaTop, eZtop)*delta_t
eZtop = eZtop/norm(eZtop) # 誤差の累積を防ぐために norm 1 に再度規格化する
# eZtop に変換する行列 Rt を作る
Rt[:,2] = eZtop
v = op( [0,0,1.0], eZtop)
v = v/norm(v)
Rt[:,1] = array(v)
Rt[:,0] = op(Rt[:,1], eZtop)
# print "Rt:\n", Rt
Itnsr = Rt * Itop * (Rt.I)
if ( indexAt % 250 == 0):
print indexAt
trjctry[indexAt,:] = eZtop
omegaTrjctry[indexAt,:] = omegaTop
Ntrjctry[indexAt,:] = N
Ltrjctry[indexAt,:] = L
putSf(trjctry, 'trajectory')
putSf(omegaTrjctry, 'omegaTrajectory')
putSf(Ntrjctry, 'nTrajectory')
putSf(Ltrjctry, 'lTrajectory')
//@@@
//copy \#####.### temp.py /v /y
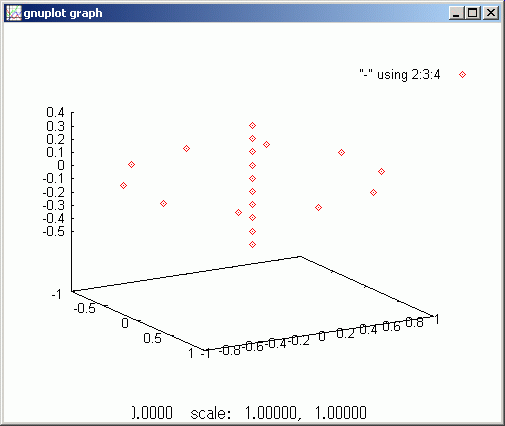
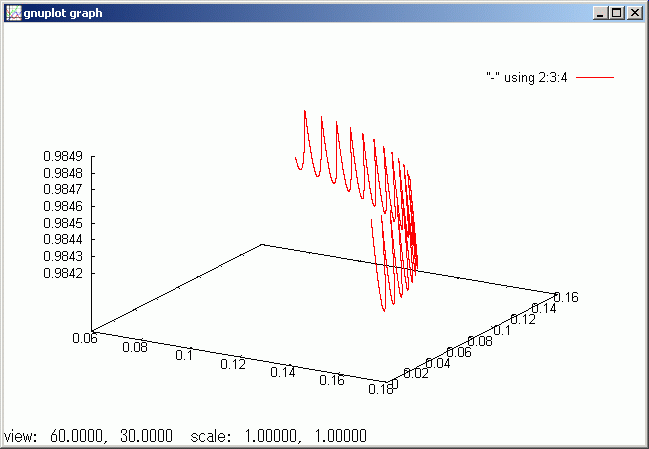
sf のときよりシミュレーション時間を 15 倍まで広げました。回転軸の軌跡は下のようになります。一回転の 1/4 程度が描かれています。
gdsp trajectory /p:16
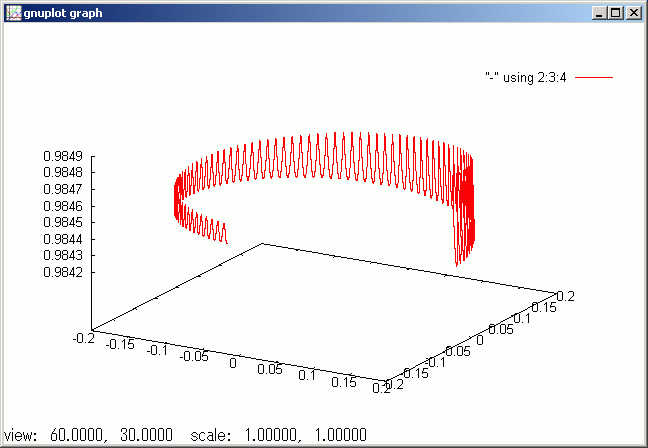
count =120000 とし、さらに四倍までにシミュレーション時間を広げて独楽の歳差運動を一周させます。z 軸の範囲が [0.9842, 0.9849] と 0.7`mm 幅であり、拡大されて表示されています。章動の振幅が小さくなっていくのには計算誤差の累積も入っています。ただし、章動が小さくなるようなピーク位置での回転軸と角速度ベクトルの位置関係も存在するので、現実の独楽でも、歳差運動は小さくなるものと思っています。
gdsp trajectory /p:16
このような計算結果を読んでいるだけではつまりません。御自分のコンピュータでも計算してみてください。時間幅をより長くしてみてください。慣性テンソルの値を変え、独楽の回転速度を変えてみてください。Gnuplot の三次元表示画像をマウスでドラッグし、様々の視点から見てください。多くの事が分かります。
Pythpn の計算結果として、回転軸ベクトル・角運動ベクトル・重力トルク*時間・角運動量ベクトルの軌跡 trajectory.val, omegaTrajectory.val, nTrajectory.val, lTrajectory.val が残されます。これを使って章動に付いて検証計算をしてみます。
sf による章動のシミュレーション計算で見られるように、シミュレーション時間全体 200`mS の 2/3 程度の所で、回転軸の先端が章動によって元の高さに近いところまで戻っています。trjctry.val ファイルを直接エディタで開き eZtop[0] 成分が最小値をとるところを探すことにより、このタイミングが 1528*0.0001`sec であることが解ります。Python によるシミュレーション計算:trajectory.val でも同じタイミングにピークがあります。eZtop の変分を計算するルーチンを変えたことによるシミュレーション数値の差が見られますが、その差は < 4.58836e-005 > と小さい事が確認できます
trjctry[1528,*] < 0.173338, 0.0100155, 0.984812 > trajectory[1528,*] < 0.173391, 0.0100189, 0.984802 > !norm(trjctry[1258,*] - trajectory[1258,*]) < 4.58836e-005 >
trajectory[1528,*] - trajectory[0,*] < -0.000257633, 0.0100189, -5.56941e-006 >
一方で角運動量に152.8`mS の間の重力トルクの比は、152.8`mS の間に独楽が倒れる角度のオーダーになるはずです。計算してみましょう。
N = @op( trajectory[0,*]0.5`meter,<0,0, -10`Kg `gH> ) 152.8`mS < -1.06886e-009, 1.30102, 0 > < -1.06886e-008, 13.0102, 0 > < -0.367507, 13.2391, 0 > lTrajectory[0,*] < 22.7305, 0.000851453, 128.911 > !norm(N)/!norm(lTrajectory[0,*]) < 0.00993907 >
この独楽が倒れない現象の直感的な説明は次のようにできます。独楽の角速度ベクトルの変化は重力トルクの方向になります。独楽が倒れる方向とは直交します。横方向に移動した角速度ベクトルは独楽の回転軸からずれてきます。独楽の回転軸は、ずれた角速度ベクトルによって回転させられます。これが積み重なって衝動となります。いったん倒れた独楽の回転軸が浮き上がってきます。その間に回転軸が横方向に動きます。sf による章動のシミュレーション計算で見られるような章動になります。
角運動量を持つ剛体を倒そうとするとき、角運動量ベクトルの向きを変化させなければならないため、角運動量に比例して倒すのに抵抗する力が発生します。でも、独楽が倒れないのは、これだけでは説明できません。章動によって倒れた独楽が引き戻されてしまいます。この運動の様子が章動としてシミュレーションでも見られています。シミュレーションでも分かるように、この章動の振幅は 1`meter の回転軸の先端で 0.7`mm です。通常サイズの独楽の運動を見ていても判らないでしょう>
独楽の理論で一番解りにくいのが、この独楽の回転軸が章動することだと思います。御自分でも様々な計算を行い考えて下さることを希望します。ここで行ったように sf を使えば計算作業自体は簡単にできます。思考に集中できます。独楽の動作の数値実験を興味のままに行って、独楽の運動理論をより深く理解して下さることを希望します。
先に実装した Python コードを使えば独楽の倒れる様子を高速にシミュレーションできます。独楽の回転速度を 100 RPM 程度まで遅くしてみましょう。高速化のためにシミュレーション時間の刻み幅を一桁小さくします。また rate を導入してサンプリング・データを小さくします。少し章動の軌跡が変わりますが、独楽の歳差運動の様子は殆ど同じです。eZtop[2] 成分が 0 より小さくなったとき独楽が倒れたと判断して python プログラムを終了させます。
//@@
# 05.06.26 PM23
# -*- encoding: cp932 -*-
from sys import*
from scipy import*
from sfVal import*
from LinearAlgebra import *
from op import *
delta_t = 0.0005
count = 10000
rate = 25
minute = 60
theta=2*pi*10/360 # 10 degree --> radian
eZtop = array([sin(theta),0,cos(theta) ])
#omegaTop = array([0,0, 50*2*pi/minute])
#omegaTop = array([0,0, 100*2*pi/minute])
#omegaTop = array([0,0, 150*2*pi/minute])
omegaTop = array([0,0, 200*2*pi/minute])
Rt = mat(reshape(zeros(3*3, Float64), (3,3) ))
Rt[0,:] = [cos(theta),0,sin(theta)]
Rt[1,:] = [0,1,0]
Rt[2,:] = [-sin(theta),0,cos(theta)]
omegaTop = mul(Rt, omegaTop)
Itop = mat(identity(3),Float64)
Itop[0,0] = 3.125 # Kg meter^2
Itop[1,1] = 3.125 # Kg meter^2
Itop[2,2] = 1.25 # Kg meter^2
Itnsr = Rt*Itop*Rt.I
L = mul(Itnsr,omegaTop)
#trjctry = reshape( zeros(3*count,Float64), (count,3) )
trjctry = reshape( zeros(3*count/rate,Float64), (count/rate,3) )
for indexAt in range(count):
# print "eZtop:",eZtop
N = op(eZtop*0.5, [ 0, 0, -10*9.806649999999999])
L = L + N* delta_t
omegaTop = mul(Itnsr.I, L)
# ω が eZtop に引き起こす回転半径は、ωtop の単位方向ベクトルと eZtop との外積で定まる。回転速度には無関係です。回転速度は phi を定めます
# Δt=0.001 以下のときは eZtop = eZtop + op(omegaTop, eZtop)*delta_t を
# 使うと誤差が累積してくる
eYtop = op(omegaTop/norm(omegaTop), eZtop)
eXtop = op(eYtop, eZtop)
omegaAbs = norm(omegaTop)
phi = omegaAbs * delta_t
eZtop = eZtop + eXtop*cos(phi) + eYtop*sin(phi) - eXtop
#eZtop = eZtop + op(omegaTop, eZtop)*delta_t
eZtop = eZtop/norm(eZtop) # 誤差の累積を防ぐために norm 1 に再度規格化する
# eZtop に変換する行列 Rt を作る
Rt[:,2] = eZtop
v = op( [0,0,1.0], eZtop)
v = v/norm(v)
Rt[:,1] = array(v)
Rt[:,0] = op(Rt[:,1], eZtop)
Itnsr = Rt * Itop * (Rt.I)
if ( indexAt % rate == 0):
print indexAt
trjctry[indexAt/rate,:] = eZtop
if (eZtop[2] <= 0):
trjctry = resize(trjctry,(indexAt/rate,3) )
break
putSf(trjctry, 'trajectory')
//@@@
//copy \#####.### temp.py /v /y
50RPM の独楽の倒れる様子です。上の python コードを働かせ
gdsp trajectory /p:16で gnuplot に表示させます。
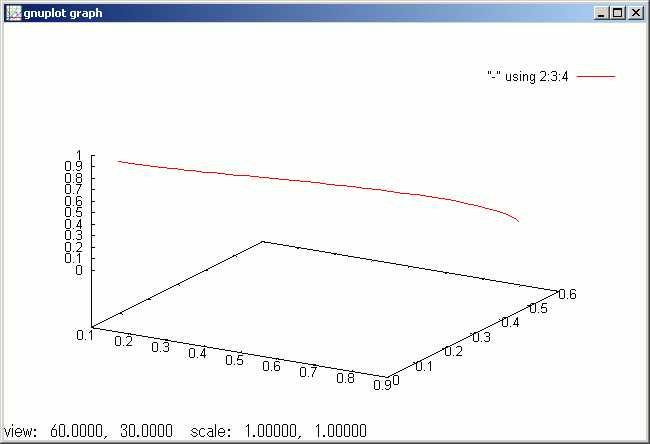
100RPM の独楽の倒れる様子です。

150RPM の独楽の歳差運動です。0 に近いところまで傾きますが、引き戻されます。
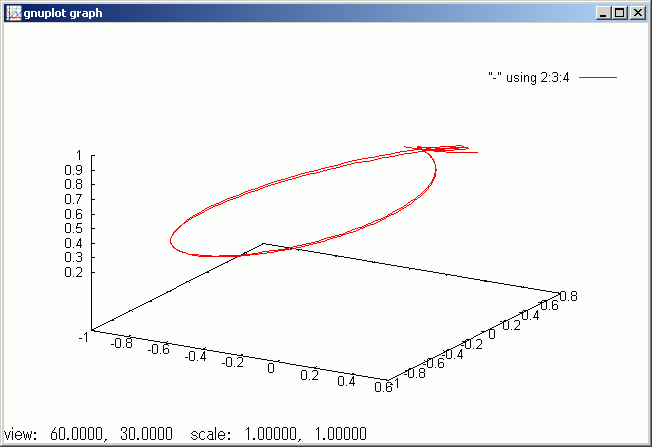
200RPM の独楽の歳差運動です。z 軸が [0,9, 0.98]`meter の範囲であり、倒れが少なくなりました。

これらを見比べていると、独楽が倒れる運動とは、歳差運動が大きくなりすぎて、倒れた独楽を引き戻す運動に入る前に地面に接触することであると分かります。
独楽を軸対象ではない薄っぺらい形にしてやると章動が働きにくくなって歳差運動しながらも倒れていくなど、パラメーターを変更してやることで、様々の独楽の運動の数値実験が楽しめます。これらの面白さは自分で興味のままに弄繰り倒すところにあります。様々の物理式の関係を自分で計算確認するところにあります。sf や python を活用して、ご自分なりの数値実験を行ってみてください。そして sf や python の威力を体験してください。sf が気に入ってもらえましたら、より高速な有償版にアップグレードしてやってください。